Я создала и активно наполняю телеграм-канал "Перець". Здесь лучшие карикатуры из журнала, начиная с 1922 года.
Заходите, подписывайтесь: https://t.me/cartalana
ШВЕЦОВ К.И., БЕВЗ Г.П."СПРАВОЧНИК ПО ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ. АРИФМЕТИКА, АЛГЕБРА", 1965
4. Биквадратное уравнение. Уравнение четвертой степени, в которое входят только четные степени неизвестного, называется биквадратным. Его записывают так:
𝑎𝑥⁴ + 𝑏𝑥² + 𝑐 = 0.
Это уравнение приводится к квадратному при помощи замены 𝑖² = 𝑧; имеем 𝑎𝑧² + 𝑏𝑧 + 𝑐 = 0. Формула решений биквадратного уравнения такова:
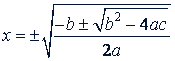
Она дает четыре корня биквадратного уравнения, а именно:
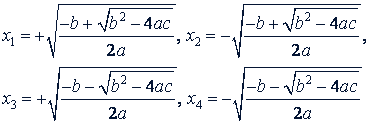
Пример. Решить уравнение 𝑧⁴ - 13𝑖² + 36 = 0.
Решение. 𝑖² = 𝑧. Получаем уравнение 𝑧² - 13𝑧 + 36 = 0. Тогда 𝑧₁ = 9, 𝑧₂ = 4. Из равенства 𝑖² = 𝑧, подставляя вместо 𝑧 найденные числа 9 и 4, получаем следующие четыре решения данного уравнения: 𝑥₁ = 3, 𝑥₂ = -3, 𝑥₃ = 2, 𝑖₄ = -2.
5. Трехчленное уравнение. Трехчленными называются уравнения вида:
𝑎𝑥2𝑛 + 𝑏𝑥𝑛 + 𝑐 = 0
(частный случай такого уравнения при 𝑛 = 2 есть биквадратное уравнение). Трехчленное уравнение с помощью замены 𝑥 ⁿ = 𝑧 приводится к квадратному уравнению
𝑎𝑧² + 𝑏𝑧 + 𝑐 = 0,
откуда
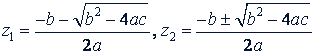
Подставив в равенство 𝑥 ⁿ = 𝑧 вместо 𝑧 его значения 𝑧₁ и 𝑧 ₂, получим два двучленных уравнения 𝑛 -й степени:
Решив, если возможно, эти двучленные уравнения, мы получим все решения данного трехчленного уравнения.
Пример. Решить уравнение 𝑥 ⁶ - 9𝑖³ + 8 = 0.
Решение, 𝑖³ = 𝑧, 𝑧² - 9𝑧 + 8 = 0. Тогда 𝑧₁ = 8 и 𝑧 ₂ = 1; следовательно, 𝑖³ = 8 и 𝑖³ = 1.
Решив эти двучленные уравнения третьей степени, получим шесть значений для 𝑥 :
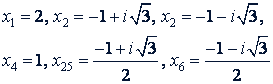
6. Симметричные уравнения. Уравнения вида
𝑎𝑥𝑛 + 𝑏𝑥𝑛 -1 + 𝑐𝑥𝑛-2 +... + 𝑐𝑥² + 𝑏𝑥 + 𝑎 = 0,
у которого коэффициенты членов, равно удаленных от начала и конца, равны, называются симметричными, или возвратными.
Например, 𝑖 ⁷ + 2𝑥 ⁶ - 5𝑥 ⁵ - 13𝑥⁴ - 13𝑖³ - 5𝑖² + 2𝑥 + 1 = 0.
Симметричное уравнение имеет следующее свойство: если число 𝑥₁ есть его решение, то обратное число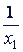 
также будет его решением (Ни один из корней симметричного уравнения не может быть равным нулю).
Симметричное уравнение может быть как четной, так и нечетной степени.
Способ решения этого уравнения четной степени покажем на при мере уравнения четвертой степени:
𝑎𝑥⁴ + 𝑏𝑥³ + 𝑐𝑥² + 𝑏𝑥 + 𝑎 = 0.
Разделив обе части уравнения на 𝑖² (так как 𝑥 ≠ 0), получим
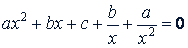
Сгруппируем члены с одинаковыми коэффициентами:
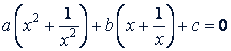
Заменяя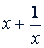 
новой буквой 𝑦, получим
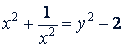
Следовательно, симметричное уравнение четвертой степени приводится к квадратному уравнению.
Симметричное уравнение четной степени можно привести с помощью подстановки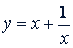 
к уравнению в два раза меньшей степени, чем степень исходного. Для этого делят все члены данного уравнения на 𝑥 ⁿ (если степень данного была 2𝑛) и группируют члены, равноотстоящие от конца и начала. После этого делают замену по формулам:
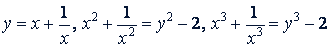и т.д.
Симметричное уравнение нечетной степени имеет корень 𝑥 = -1. Если это уравнение поделить на 𝑖 + 1, то получится симметричное уравнение четной степени, на единицу меньше степени исходного уравнения.
Таким образом, всякое симметричное уравнение нечетной степени приводится к двум уравнениям: 𝑥 + 1 = 0 и симметричному уравнению четной степени, на единицу меньше степени исходного уравнения.
Рассмотренные выше уравнения называют симметричными уравнениями первого рода.
Уравнения вида
𝑎𝑥2𝑘 + 𝑏𝑥2𝑘-1 + 𝑐𝑥2𝑘-2 +... + 𝑑𝑥𝑘+1 + 𝑙𝑥𝑘 -𝑑𝑥𝑘-1 +... + (-1)𝑘-1 𝑏𝑥 + (-1)𝑘𝑎 = 0
называются симметричными уравнениями второго рода. Решаются эти уравнения тем же методом, но новое неизвестное 𝑦 связывается с 𝑥 соотношением
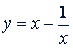
Пример. Решить уравнение
2𝑖 ⁵ + 5𝑖⁴ - 13𝑖³ - 13𝑖² + 5𝑥 + 2 = 0.
Решение. Это симметричное уравнение нечетной степени, следовательно, оно имеет корень 𝑥 = -1. Разделим многочлен, имеющийся в левой части данного уравнения, на 𝑖 + 1:
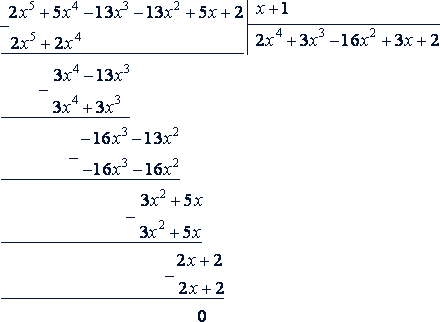
Следовательно, для определения остальных корней данного уравнения надо решить уравнение
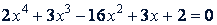
или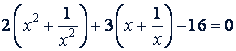 
Полагая 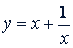, получим 2(𝑦² - 2) + 3𝑦 - 16 = 0, откуда 𝑦₁ = -4, 𝑦 ₂ = 2,5.
Следовательно, 𝑖² + 4𝑥 + 1 =0 и 2𝑖² - 5𝑥 + 2 = 0.
Ответ.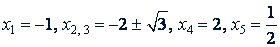 
1. Множества. Теория соединений, или, как ее еще называют, комбинаторика, - это раздел элементарной алгебры, где изучаются некоторые операции над конечными множествами и решаются задачи, связанные с этими операциями.
Понятия множества - одно из неопределяемых основных понятий в математике. С этим понятием встречаемся во всех ее разделах. Так, в арифметике рассматривают множество натуральных чисел, множество простых чисел; в алгебре - множество многочленов, корней данного уравнения и т.п. Объекты, составляющие множество, называются элементами этого множества. Множество, состоящее из конечного числа элементов, называется конечным. Такими множествами являются множество всех двузначных чисел, множество вершин данного многоугольника, множество его диагоналей и т.д. Множество, содержащее неограниченное количество элементов, называется бесконечным. Бесконечным множеством, например, является множество всех натуральных чисел, всех простых чисел и т.д.
Множество, не содержащее элементов, называется пустым.
Если всякий элемент множества 𝑎 есть элементом множества 𝐵, то множество 𝑎 называют подмножеством множества 𝑏. Подмножеством множества 𝐵 считают также пустое множество и само множество 𝐵; их называют несобственными подмножествами; остальные подмножества называют собственными.
Множество 𝑀 = {𝑎, 𝑏, 𝑐, 𝑑, ...} называется упорядоченным, если между его элементами установлено некоторое соотношение 𝑎 < 𝑏 (читают: " 𝑎 предшествует 𝑏 "), имеющее следующие свойства:
1) для каких-либо двух элементов 𝑎 и 𝑏 действительно одно и только одно из соотношений 𝑎 = 𝑏, 𝑎 < 𝑏, 𝑏 > 𝑎;
2) для всяких трех элементов 𝑎, 𝑏 и 𝑐 из соотношений 𝑎 > 𝑏 и 𝑏 > 𝑐 следует соотношение 𝑎 > 𝑐.
2. Перестановки. Пусть мы имеем множество 𝑀, состоящее из 𝑛 элементов: 𝑎₁, 𝑎 ₂, 𝑎 ₃, ..., 𝑎𝑛. Если переставлять эти элементы все возможными способами, оставляя неизменным их общее число, получим несколько последовательностей:
𝑎1 𝑎2 𝑎3... 𝑎𝑛,
𝑎2 𝑎1 𝑎3... 𝑎𝑛,
𝑎𝑛 𝑎3 𝑎2... 𝑎1 и т.д. (Записывая перестановки, обычно между их членами не ставят запятых. Однако на приведенный выше записи ни в коем случае нельзя смотреть как на произведения)
Каждую из этих последовательностей называют перестановкой из данных 𝑛 элементов.
Пример. Ниже приведены 6 всевозможных перестановок из букв 𝑎, 𝑏 и 𝑐 :
𝑎𝑏𝑐, 𝑎𝑐𝑏, 𝑏𝑎𝑐, 𝑏𝑐𝑎, 𝑐𝑎𝑏, 𝑐𝑏𝑎.
Итак, перестановкой из 𝑛 элементов называется всякая конечная последовательность, которая получается в результате упорядоченности некоторого конечного множества, состоящего из 𝑛 элементов.
Если множество имеет некоторое число элементов, то его можно упорядочить несколькими способами. Число всех перестановок из 𝑛 элементов обозначается 𝑝𝑛. Это число равно произведению всех целых чисел от 1 до 𝑛 включительно:
𝑝𝑛 = 1 · 2 · 3 · 4... (𝑛 - 1) 𝑛.
Произведение 𝑛 первых натуральных чисел принято обозначать символом 𝑛 !:
1 · 2 · 3 · 4 · 5 ·... · 𝑛 = 𝑛 !
Символ 𝑛 ! читают "эн факториал". Это слово происходит от латинского factor, что значит множитель.
Примечание. При 𝑛 = 1 в выражении 1 · 2 · 3, ... 𝑛 остается одно число 1. Поэтому принимается (в качестве определения), что 1! = 1. При 𝑛 = 0 выражение 1 · 2, ..., 𝑛 вовсе лишается смысла. Однако принимается (в качестве определения), что 0! = 1.
Итак, 𝑝𝑛 = 𝑛 !
Верна также следующая формула:
𝑝𝑛 = 𝑛 · 𝑝𝑛 -1
Пример. Каким числом способов можно рассадить 8 зрителей в ряду из 8 мест?
Решение. 𝑝8 = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 = 40320.
3. Сочетания (комбинации). Пусть имеем множество 𝑀, состоящее из 𝑛 различных элементов.
Всякое подмножество множества 𝑀, содержащее 𝑘 элементов (𝑘 = 0, 1, 2, ..., 𝑛), называется сочетанием или комбинацией из данных 𝑛 элементов по 𝑘 элементов.
Из определения следует, что два различных сочетания из данных 𝑛 элементов по 𝑘 элементов отличаются по крайней мере одним элементом.
Пример. Из множества цифр 1, 2, 3, 4 можно образовать такие сочетания по два элемента: 1, 2; 1, 3; 1, 4; 2, 3; 2, 4; 3, 4.
Число различных сочетаний из 𝑛 элементов по 𝑘 обозначается символом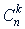 
(combinatio от combinare (лат.) - соединять). Но иногда вместо 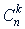пишут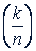 
.
Число всех сочетаний из 𝑛 элементов по 𝑘 элементов, где 1 ≤ 𝑘 ≤ 𝑛, равно произведению 𝑘 последовательных натуральных чисел, из которых наибольшее есть 𝑛, деленному на произведение последовательных натуральных чисел от 1 до 𝑘
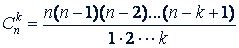
Формулу для 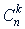можно записать в ином виде. Умножив числитель и знаменатель дроби в правой части ее на произведение 1 · 2 · 3... (𝑛 - 𝑘), получим
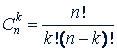
или
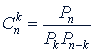
⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨
МЕНЮ САЙТА / СОДЕРЖАНИЕ