Я создала и активно наполняю телеграм-канал "Перець". Здесь лучшие карикатуры из журнала, начиная с 1922 года.
Заходите, подписывайтесь: https://t.me/cartalana
ШВЕЦОВ К.И., БЕВЗ Г.П."СПРАВОЧНИК ПО ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ. АРИФМЕТИКА, АЛГЕБРА", 1965
47. Исторические сведения о комплексных числах
Числа, впоследствии получившие наименование комплексных, впервые появились в одной из задач Д. Кардано. Назвал он их "софистическими" числами, желая этим подчеркнуть их парадоксальность: считалось, что корень квадратный из отрицательного числа не имеет смысла, и в то же время произведение двух таких корней оказалось вполне реальным числом.
Начало применению комплексных чисел в математике положили Г. Лейбниц и И. Бернулли. Лейбниц утверждал, что логарифмы отрицательных чисел существуют и являются комплексными числами. И. Бернулли и Даламбер пытались доказать, что они действительны. Этот спорный вопрос удалось решить Л. Эйлеру. Он показал, что логарифмы отрицательных и комплексных чисел - числа мнимые.
В нескольких заметках, вышедших в первой четверти XVIII в., А. Муавр указал на связь, существующую между комплексными числами и тригонометрическими функциями, и вывел, правда, в неявной форме, свою знаменитую формулу. В явной форме:
(cos φ ± 𝑖 sin φ)ⁿ = cos 𝑛 φ ± sin 𝑛 φ;
эта формула была выведена Л. Эйлером в 1748 г. Несколько раньше, в 1740-1743 гг., Л. Эйлер установил основное соотношение, связывающее показательную и тригонометрические функции:
𝑒𝑥𝑖 = cos 𝑥 + 𝑖 sin 𝑥.
Со второй половины XVIII в. началась уже интенсивная разработка вопросов, связанных с понятием комплексного числа. Начало систематического использования комплексных чисел связано с работами Эйлера и Даламбера, которые выяснили ряд свойств комплексных чисел и их связь с некоторыми задачами геодезии, картографии, гидродинамики.
Однако, несмотря на все достижения теории, математики отказывались считать комплексные числа реально существующими. Основным противоречием была невыясненность самого понятия мнимой единицы: с одной стороны, было известно, что не существует числа, квадрат которого был бы равен -1, и в то же время действия с такого рода "мнимыми" числами приводили к правильным результатам. Таким образом, надо было или признать, что комплексные числа являются своего рода условностью, или же найти их истолкование, связанное с объективной реальностью. Подобное геометрическое истолкование и было найдено в самом конце XVIII в.
Впервые геометрическое изображение комплексных чисел было предложено Г. Кюном, учителем гимназии в Данциге в 1750-1751 гг. Однако только в 1799 г. норвежский математик Гаспар Вессель (1745-1818) дал общее геометрическое истолкование комплексных чисел как точек на плоскости. Существенным было то, что Вессель показал, что все известные до того времени числа являются лишь частными случаями комплексных.
В начале XIX в. над вопросами дальнейшего обоснования теории комплексных чисел работали К.Ф. Гаусс и О. Коши. К.Ф. Гаусс ввел и сам термин "комплексные числа".
1. Некоторые общие теоремы. Уравнениями высших степеней называются алгебраические уравнения степени выше второй. Общий вид таких уравнений:
𝑎0𝑥𝑛 + 𝑎1𝑥𝑛-1 +... + 𝑎𝑛 -1𝑥 + 𝑎𝑛 = 0.
а) Всякое алгебраическое уравнение 𝑛-й степени в множестве комплексных чисел имеет 𝑛 корней, среди которых могут быть и равные друг другу.
б) Если многочлен 𝑓(𝑥) = 𝑎0 𝑥𝑛 + 𝑎1𝑥𝑛 -1 + ... + 𝑎𝑛-1 𝑥 + 𝑎𝑛 имеет корень 𝑥1 то он делится на 𝑥 - 𝑥1, т.е. 𝑓(𝑥) = (𝑥 - 𝑖1)𝑞(𝑖). Это - следствие из теоремы Безу: остаток от деления многочлена 𝑓(𝑥) на 𝑥 - 𝑥1 равен 𝑓(𝑖1).
в) Всякий многочлен 𝑛-й степени в множестве комплексных чисел может быть представлен и притом единственным способом в виде произведения двучленов первой степени:
𝑓(𝑖) = 𝑎(𝑥 - 𝑥1)𝑚(𝑥-𝑖2)𝑝 ... (𝑥 - 𝑥𝑛)𝑟,
где 𝑖1, 𝑥2, ..., 𝑥𝑛 - корни данного уравнения, а 𝑚 + 𝑝 + ... + 𝑟 = 𝑛.
г) Если уравнение с действительными коэффициентами (а только такие и рассматриваются в элементарной алгебре) имеет комплексный корень 𝑎 + 𝑏𝑖, то оно имеет и сопряженный с ним корень 𝑎 - 𝑏𝑖. Если же это уравнение нечетной степени, то оно должно иметь хотя бы один действительный корень.
д) Всякое уравнение с действительными коэффициентами имеет четное число мнимых корней попарно сопряженных.
е) Как уже отмечалось, для квадратного уравнения 𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0 справедлива теорема Виета: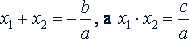 
где 𝑥1 и 𝑥2 - корни уравнения.
Вообще для уравнения 𝑛-й степени
𝑎0𝑖𝑛 + 𝑎1𝑖𝑛-1 + 𝑎2 𝑖𝑛-2 + ... + 𝑎𝑛-1𝑖 + 𝑎𝑛 = 0
имеем:
,
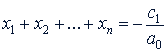а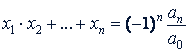 
ж) Для того чтобы несократимая дробь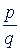 
была корнем уравнения с целыми коэффициентами
𝑎0𝑖𝑛 + 𝑎1𝑖𝑛-1 + ... + 𝑎𝑛-1𝑖 + 𝑎𝑛 = 0
необходимо, чтобы 𝑝 было делителем свободного члена 𝑎𝑛, a 𝑞 - делителем коэффициента 𝑎0.
з) Если уравнение имеет целые коэффициенты и коэффициент при 𝑥𝑛 равен 1, то рациональными корнями могут быть только целые числа.
и) Целые корни уравнения с целыми коэффициентами являются делителями свободного члена.
В некоторых случаях, используя изложенные выше свойства, можно легко решать уравнения высших степеней с целыми коэффициентами.
Пример 1. Решить уравнение 𝑖³ + 6𝑖² + 11𝑥 - 6 = 0.
Решение. Так как уравнение имеет целые коэффициенты и коэффициент при 𝑥³ равен единице, то целыми корнями могут быть только делители свободного члена, т.е.
1; 2; 3; -1; -2; 3.
Проверим, не является ли 1 корнем данного уравнения:
𝑓 (1) = 1³ - 6 · 1² + 11 · 1 - 6 = 0.
Тогда на основании теоремы Безу полином в левой части имеет делителем 𝑥 - 1.
Можно или непосредственно разделить левую часть на 𝑥 - 1 или элементарным приемом представить в виде произведения:
𝑖³ - 𝑖² - 5𝑖² + 5𝑥 + 6𝑖 - 6 = 𝑖²(𝑥 - 1) - 5𝑥 (𝑥 - 1) + 6(𝑖 - 1) = (𝑥 - 1)(𝑖² - 5𝑥 + 6).
Квадратный трехчлен легко разлагается на множители, следовательно,
𝑓 (𝑥) = (𝑥 - 1)(𝑥 - 2)(𝑥 - 3) = 0.
Отсюда получаем, что корни данного уравнения будут 1; 2; 3.
Некоторые алгебраические уравнения высших степеней можно решить, сведя их к квадратному.
2. Уравнения, левая часть которых разлагается на множители, а правая есть нуль. В этом случае левую часть уравнения разлагают на множители, из которых каждый - многочлен не выше второй степени. Тогда приравниваем нулю каждый множитель в отдельности и решаем полученные уравнения. Найденные корни будут корнями исходного уравнения.
Пример. Решить уравнение 𝑖³ + 3𝑖² - 10𝑖 = 0.
Решение. Левая часть легко разлагается на множители 𝑥 и 𝑖² + 3𝑖 - 10 и, следовательно, распадается на два уравнения
𝑥 = 0 и 𝑖² + 3𝑥 - 10 = 0,
из которых находим три решения:
𝑖₁ = 0, 𝑖 ₂ = 2, 𝑖 ₃ = -5.
Эффективность решения уравнений этим способом зависит от умения разложить левую часть уравнения на множители. Проиллюстрируем это на примерах.
Примеры.
Решить уравнения:
а) 𝑖³ + 6 = 7𝑥; б) 𝑖³ - 4𝑖² - 4𝑥 - 5 = 0;
в) 𝑖³ + (𝑏² - 𝑎²) 𝑥 + 𝑎𝑏² = 0; г) 𝑖⁴ + 2𝑖³ - 13𝑖² - 14𝑖 + 24 = 0.
Решение.
а) 𝑖³ - 7𝑖 + 6 = 0; 𝑖³ - 𝑖 - 6𝑖 + 6 = 0; (𝑖³ - 𝑥) - (6𝑥 - 6) = 0;
𝑖²(𝑥 - 1) - 6 (𝑥 - 1) = 0; (𝑥 - 1)(𝑖² - 6) = 0.
Тогда
𝑖 - 1 = 0 и 𝑖² - 6 = 0.
Значит,
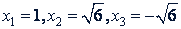
б) 𝑖³ - 5𝑖² + 𝑖² - 5𝑥 + 𝑥 - 5 = 0; 𝑖²(𝑖 - 5) + 𝑖 (𝑥 - 5) + (𝑥 - 5) = 0; (𝑥 - 5)(𝑖² + 𝑖 + 1) = 0.
Тогда
𝑥 - 5 = 0 и 𝑖² + 𝑥 + 1 = 0.
Значит,
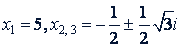
в) 𝑖³ + 𝑏² 𝑥 - 𝑎² 𝑥 + 𝑎𝑏² = 0; (𝑖³ - 𝑎² 𝑥) + (𝑏² 𝑥 + 𝑎𝑏²) = 0; 𝑖 (𝑖² - 𝑎²) + 𝑏²(𝑥 + 𝑎) = 0; 𝑖 (𝑖 - 𝑎)(𝑥 + 𝑎) + 𝑏²(𝑥 + 𝑎) = 0; (𝑖 + 𝑎)[𝑥 (𝑥 - 𝑎) + 𝑏²] = 0; (𝑥 + 𝑎)(𝑖² - 𝑎𝑥 + 𝑏²) = 0.
Тогда
𝑥 + 𝑎 = 0 и 𝑖² - 𝑎𝑥 + 𝑏² = 0.
Значит,
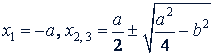
г) (𝑥⁴ + 𝑖³ - 12𝑖²) + (𝑖³ + 𝑖² - 12𝑖) + (-2𝑖² - 2𝑥 + 24) = 0; 𝑖²(𝑖² + 𝑖 - 12) + 𝑥 (𝑖² + 𝑥 - 12) - 2(𝑖² + 𝑥 - 12) = 0; (𝑖² + 𝑥 - 12)(𝑖² + 𝑖 - 2) = 0.
Тогда
𝑖² + 𝑥 - 12 = 0 и 𝑖² + 𝑥 - 2 = 0.
Значит,
𝑖₁ = 3, 𝑖 ₂ = -4, 𝑖 ₃ = 1, 𝑖 ₄ = -2.
Проверка. По теореме Виета:
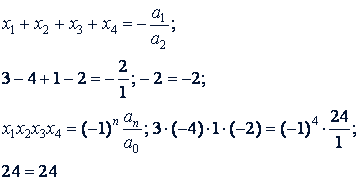
3. Двучленные уравнения. Двучленным уравнением называется уравнение вида 𝑎𝑥𝑚 + 𝑏 = 0, (𝑎 ≠ 0). Разделив обе части такого уравнения на а, получим приведенное двучленное уравнение 𝑥𝑚 ± 𝑞 = 0. Чтобы решить такие уравнения, полагают, что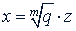 
; тогда эти уравнения приводятся к более простым:
𝑧𝑚 - 1 = 0, 𝑧𝑚 + 1 = 0.
Решение таких уравнений элементарными способами может быть выполнимо при некоторых частных значениях 𝑚. Общий прием состоит в разложении левой части уравнения на множители, после чего уравнение приводится к виду, рассмотренному нами раньше (Когда уравнение имеет вид 𝑎𝑥𝑚 + 𝑏𝑥𝑛 = 0, где 𝑚 > 𝑛, то его можно представить так: 𝑥𝑛(𝑎𝑥𝑚 - 𝑛 + 𝑏) = 0 и, следовательно, оно распадается на два уравнения: 𝑖𝑛 = 0 и 𝑎𝑥𝑚 - 𝑛 + 𝑏 = 0).
Примеры. Решить уравнения:
а) 𝑖³ - 1 = 0;
б) 16𝑖⁴ + 81 = 0.
Решение.
а) 𝑖³ - 1 = (𝑥 - 1)(𝑖² + 𝑥 + 1).
Значит уравнение 𝑖³ - 1 = 0 имеет своими корнями корни уравнений 𝑖 - 1 = 0 и 𝑖² + 𝑖 + 1 = 0.
Решив их, найдем, что уравнение 𝑖³ - 1 =0 имеет следующие три корня:
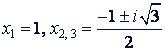
б) Разделив обе части данного уравнения на 16, получим
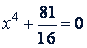
Пусть
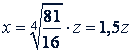
тогда
𝑧⁴ + 1 =0.
Это уравнение можно решать несколькими способами.
Первый способ.
𝑧⁴ = -1, 𝑧² = ± 𝑖,
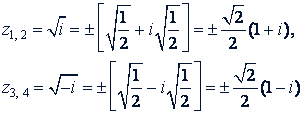
Второй способ.
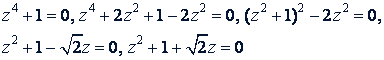
откуда
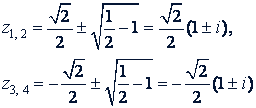
Третий способ.
где 𝑘 = 0, 1, 2, 3,
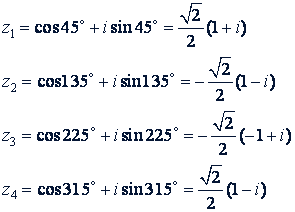
Графически корни уравнения 𝑧⁴ + 1 = 0 можно изобразить, как показано на рис. 81. Корни данного уравнения получим, если аргументы чисел 𝑧₁ 𝑧 ₂, 𝑧 ₃, 𝑧 ₄ умножим на 1,5.
Ответ.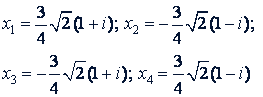 
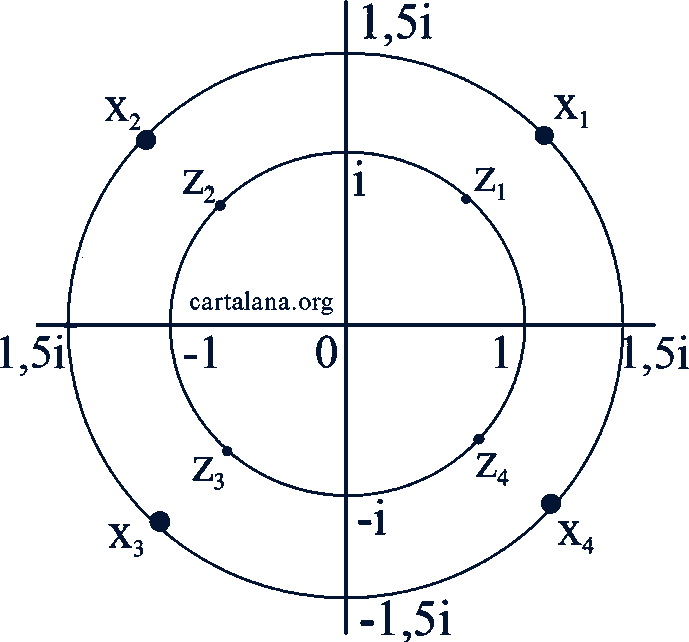
Рис. 81
⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨
МЕНЮ САЙТА / СОДЕРЖАНИЕ