Ł Старые понятные учебники советских времен по физике, математике. Акупунктура, похудение

ШВЕЦОВ К.И., БЕВЗ Г.П."СПРАВОЧНИК ПО ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ. АРИФМЕТИКА, АЛГЕБРА", 1965

2. Умножение. Пусть даны два комплексных числа 𝑧₁ и 𝑧 ₂. Записав их в тригонометрической форме

𝑧₁ = 𝑟₁(cos φ₁ + 𝑖 sin φ₁); 𝑧 ₂ = 𝑟 ₂(cos φ₂ + 𝑖 sin φ₂)

и перемножив, получим:

𝑧₁ 𝑧 ₂ - 𝑟₁ 𝑟 ₂[cos (φ₁ + φ₂) + 𝑖 sin (φ₁ + φ₂)].

Следовательно, модуль произведения двух комплексных чисел равен произведению модулей сомножителей, а аргумент равен сумме аргументов сомножителей. Это правило верно и для любого числа сомножителей.

Пример.

а) Пусть

𝑧₁ = 3(cos 20° + 𝑖 sin 20°);

𝑧 ₂ = 2(cos 35° + 𝑖 sin 35°),

тогда

𝑧₁ 𝑧 ₂ = 6(cos 55° + 𝑖 sin 55°).

б) Перемножить

2(cos 150° + 𝑖 sin 150°), 3 [cos (-160°) + 𝑖 sin (-160°)]

и 0,5(cos 10° + 𝑖 sin 10°).

Решение. Модуль произведения 2 · 3 · 0,5 = 3. Аргумент произведения 150°- 160° + 10° = 0°. Произведение равно 3(cos 0°+ 𝑖 sin 0°).

в) Перемножить

𝑟 (cos φ + 𝑖 sin φ) · 𝑟 [cos (-φ) + 𝑖 sin (-φ)] = 𝑟² (cos 0° + 𝑖 sin 0°) = 𝑟²,

значит произведение двух сопряженных комплексных чисел есть действительное число, равное квадрату их общего модуля.

3. Деление. Пусть требуется число 𝑧₁ = 𝑟₁(cos φ₁ + 𝑖 sin φ₁) разделить на число 𝑧 ₂ = 𝑟 ₂(cos φ₂ + 𝑖 sin φ₂).

Будем иметь

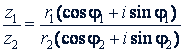
Умножив числитель и знаменатель на cos φ₂ - 𝑖 sin φ₂ после преобразований, получим

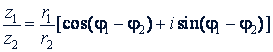
Следовательно, модуль частного двух комплексных чисел равен частному модулей, а аргумент - разности аргументов делимого и делителя.

Пример. Пусть

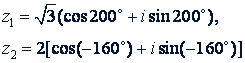
Тогда

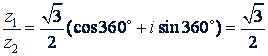
4. Возведение в степень. Умножая число 𝑧 = 𝑟 (cos φ + 𝑖 sin φ) само на себя 𝑛 раз, по правилу умножения комплексных чисел, получаем

𝑧 ⁿ = [𝑟 (cos φ + 𝑖 sin φ]ⁿ = 𝑟 ⁿ(cos 𝑛 φ + 𝑖 sin 𝑛 φ).

Значит, модуль степени комплексного числа равен той же степени модуля основания, а аргумент равен аргументу основания, умноженному на показатель степени.

В частном случае, если 𝑟 = 1, то предыдущее равенство принимает вид:

(cos φ + 𝑖 sin φ)ⁿ = cos 𝑛 φ + 𝑖 sin 𝑛 φ.

Эта формула носит название формулы Муавра, по имени английского математика Муавра (1667-1754). Примеры.

а) Возвести в куб число

𝑧 = 2(cos 20° + 𝑖 sin 20°).

Решение.

так как

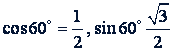
б) Возвести в 20-ю степень число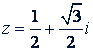

Решение. Записав его в тригонометрической форме

𝑧 = 1(cos 60° + 𝑖 sin 60°),

найдем:

в) Найти выражение косинуса и синуса угла 3φ через косинус и синус угла φ.

Решение.

cos 3φ + 𝑖 sin 3φ = (cos φ + 𝑖 sin φ)³ = cos³ φ + 3𝑖 cos² φ sin φ + 3𝑖² cos φ sin² φ + 𝑖³ sin³ φ = cos³ φ - 3 cos φ sin² φ + 𝑖 (3 cos² φ sin φ - sin³ φ).

Приравнивая действительные и мнимые части, получаем:

cos 3φ = cos³ φ - 3sin² φ cos φ; sin 3φ = 3 cos² φ sin φ - sin³ φ.

Примечание. Можно так же найти cos 4φ, sin 4φ и общие формулы для sin 𝑛 φ, cos 𝑛 φ.

5. Извлечение корня. Корень 𝑛 -й степени из комплексного числа извлекается с помощью формулы

Здесь 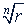арифметический, a 𝑘 = 0, 1, 2, ..., 𝑛 - 1. Корень степени 𝑛 в множестве комплексных чисел имеет 𝑛 различных значений. Исключение представляет 𝑧 = 0. В этом случае все значения корня равны между собой и равны нулю.

Модуль корня 𝑛 -й степени из комплексного числа равен корню той же степени из модуля подкоренного числа, а аргумент для каждого значения корня определяется по формуле

где 𝑘 = 0, 1, 2, ..., 𝑛 - 1.

Пример 1. Найти корень кубический из числа

𝑧 = 𝑟 (cos φ + 𝑖 sin φ).

Решение.

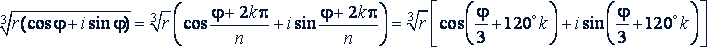
При 𝑘 = 0 имеем:

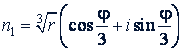
При 𝑘 = 1:

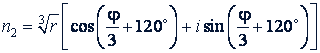
При 𝑘 = 2:

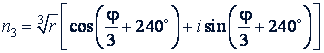
Heтрудно убедиться, что при 𝑘 = 3, 4, 5, 6, ... будем получать 𝑛₄ = 𝑛₁, 𝑛₅ = 𝑛₂, и т.д., т.е. новых значений корня мы уже не получим.

Пример 2. Найти кубический корень из единицы.

Решение. Имеем

1 = 1(cos 360° 𝑘 + 𝑖 sin 360° 𝑘).

Тогда

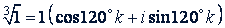
При 𝑘 = 0, 1, 2 получим соответственно:

6. Геометрическое истолкование действий над комплексными числами. Сложение. Пусть требуется сложить числа 𝑧₁ = 𝑎₁ + 𝑏₁ 𝑖 и 𝑧 ₂ = 𝑎 ₂ + 𝑏 ₂ 𝑖. Числу 𝑧₁ соответствует вектор 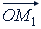, а числу 𝑧 ₂ - вектор (рис. 74). Из конца 𝑀₁ вектора 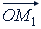проведем вектор 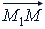, равный вектору , т.е. такой, который имеет с вектором одинаковую длину и направление. Тогда вектор 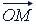даст геометрическое изображение суммы 𝑧₁ + 𝑧 ₂. Если векторы 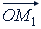и лежат на одной прямой, то и вектор 𝑂𝑀 лежит на той же прямой (рис. 75 и 76).

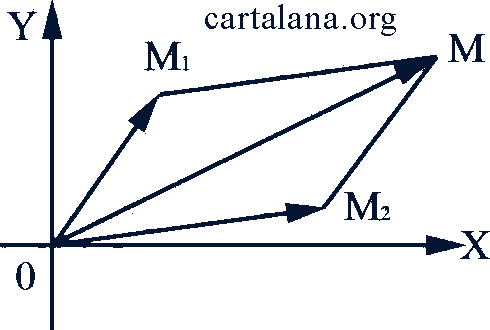
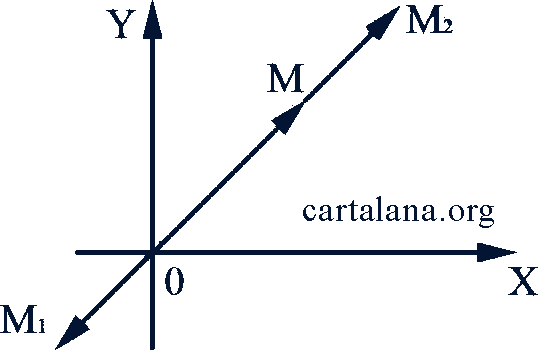
Рис. 74-75-76

Построенный вектор 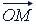называется суммой векторов 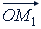и . Итак, сумма двух комплексных чисел представляется суммой векторов, изображающих отдельные слагаемые.

Сумма трех (и большего числа) комплексных чисел также представляется суммой векторов, изображающих отдельные слагаемые.

Вычитание. Пусть требуется вычесть число 𝑧₂ = 𝑎₂ + 𝑏₂𝑖 из числа 𝑧₁ = 𝑎₁ + 𝑏₁𝑖. Числу 𝑧₁ геометрически соответствует вектор 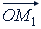, а числу 𝑧₂ - вектор (рис. 77). Чтобы получить вектор, соответствующий разности 𝑧₁ - 𝑧₂, преобразуем эту разность: 𝑧₁ - 𝑧₂ = 𝑧₁ + (-𝑧₂). Точка 𝑀₃, соответствующая (-𝑧₂), получается из точки 𝑧₂ посредством преобразования симметрии относительно начала 0. Тогда вектор 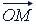соответствует числу 𝑧₂-𝑧₁.

Рис. 77

Построенный вектор 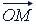называется разностью векторов и .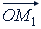

Итак, разность двух комплексных чисел представляется разностью двух векторов, изображающих уменьшаемое и вычитаемое.

Умножение. Чтобы построить вектор 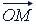, соответствующий произведению 𝑧₁𝑧₂, где 𝑧₁ = 𝑟 (cos φ₁ + 𝑖 sin φ₁) и 𝑧₂ = 𝑟 (cos φ₂ + 𝑖 sin φ₂), достаточно вектор 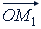, соответствующий числу 𝑧₁ повернуть на угол φ₂ и подвергнуть его преобразованию растяжения (или сжатия, если 𝑟₂ < 1) в 𝑟₂ раз (рис. 78).

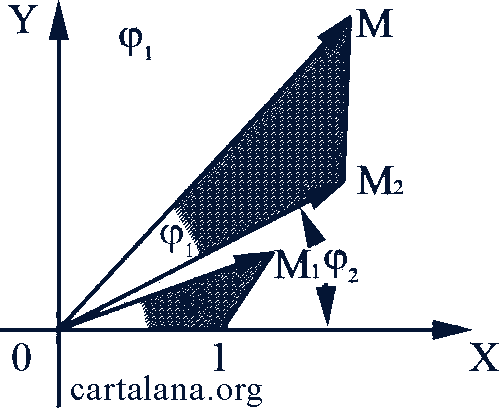
Рис. 78

Если 𝑟₂ = 1, то вектор 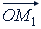можно будет только повернуть на угол φ₂

Деление. Так как деление можно представить как умножение 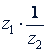, то способ построения вектора 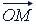, соответствующего числу 𝑧, будет следующий: вектор 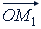, соответствующий числу 𝑧₁ достаточно повернуть на угол φ₂ и подвергнуть операции сжатия (или растяжения, если 𝑟₂ < 1) в 𝑟₂ раз (рис. 79).

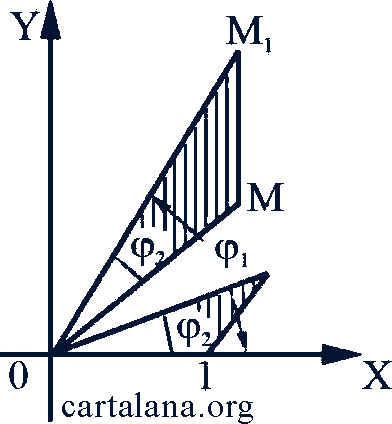
Рис. 79

Здесь 𝑟₂ и φ₂ - модуль и аргумент 𝑧₂. Если 𝑟₂ = 1, то вектор 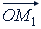только повернется на угол φ₂.

Извлечение корня. Если 𝑧 = 𝑟 (cos φ + 𝑖 sin φ), то

где 𝑘 = 1, 2, 3, ..., 𝑛 - 1.

Отсюда следует, что все 𝑛 различных значений величины 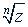имеют один и тот же модуль , а аргументы двух значений 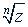, соответствующие соседним значениям 𝑘 (𝑘 и 𝑘 + 1), отличаются один от другого на 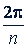и поэтому точки, соответствующие значениям 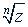, являются вершинами правильного 𝑛-угольника, вписанного в окружность радиуса с центром в начале координат.

Способ построения точек, соответствующих значениям 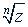, таков (рис. 80). Из начала координат, как из центра, описываем окружность, радиус которой равен . Проведя из начала координат луч, направленный к положительному направлению действительной оси под углом в 𝑛 раз меньшим, чем угол, образованный с тем же направлением луча, идущим из начала координат в точку 𝑧, мы найдем на окружности точку, соответствующую значению 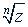при 𝑘 = 0. Вписав в окружность правильный 𝑛 -угольник так, чтобы одной из его вершин была найденная точка, мы построим точки, соответствующие остальным значениям корня.

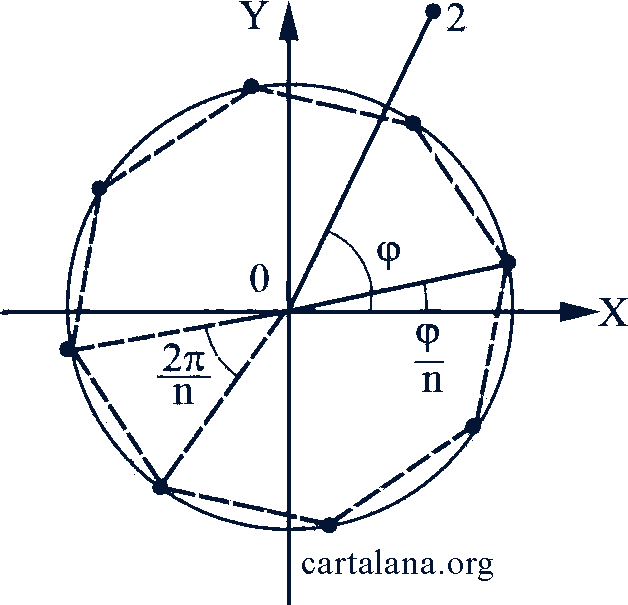
Рис. 80

⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨

МЕНЮ САЙТА / СОДЕРЖАНИЕ