Ł Старые понятные учебники советских времен по физике, математике. Акупунктура, похудение

ШВЕЦОВ К.И., БЕВЗ Г.П."СПРАВОЧНИК ПО ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ. АРИФМЕТИКА, АЛГЕБРА", 1965

Примечание. Относительно комплексных чисел не принято никакого соглашения, какое из них считать больше другого.

2. Действия над комплексными числами. Над комплексными числами производятся такие же действия, как и над вещественными. Чтобы произвести какое-нибудь действие над комплексными числами вида 𝑎 + 𝑏𝑖, надо произвести действия над двучленами такого вида по тем правилам, которые известны для двучленов с вещественными членами, и, наконец, в результате заменить везде 𝑖² на -1. Исходя из этого, действия над комплексными числами определяются так.

Сложение. Суммой комплексных чисел 𝑎 + 𝑏𝑖 и 𝑎' + 𝑏'𝑖 называется комплексное число (𝑎 + 𝑎') + (𝑏 + 𝑏') 𝑖.

Отсюда следует, что сумма сопряженных комплексных чисел 𝑎 + 𝑏𝑖 и 𝑎 - 𝑏𝑖 равна действительному числу (Сумма двух несопряженных комплексных чисел тоже может быть действительным числом, например (7 + 3𝑖) + (2 - 3𝑖) = 9) 2𝑎, комплексное число 𝑎 + 𝑏𝑖 можно рассматривать как сумму вещественного числа а и чисто мнимого числа 𝑏𝑖.

Примеры. (4 + 2𝑖) + (-3 + 𝑖) = 1 + 3𝑖; (0 + 2𝑖) + (0 + 5𝑖) = 0 + 7𝑖, т.е. 2𝑖 + 5𝑖 = 7𝑖; (-5 + 8𝑖) + (-3 - 8𝑖) = -8.

Для сложения комплексных чисел справедливы те же основные законы, что и для вещественных чисел:

(𝑎 + 𝑏𝑖) + (𝑐 + 𝑑𝑖) = (𝑐 + 𝑑𝑖) + (𝑎 + 𝑏𝑖)

[(𝑎 + 𝑏𝑖) + (𝑐 + 𝑑𝑖)) + (𝑚 + 𝑛𝑖) = (𝑎 + 𝑏𝑖) + [(𝑐 + 𝑑𝑖) + (𝑚 + 𝑛𝑖)].

Вычитание. Исходя из определения вычитания как действия, обратного сложению, разность комплексных чисел 𝑎 + 𝑏𝑖 и 𝑎' + 𝑏'𝑖 находят так:

(𝑎 + 𝑏𝑖) - (𝑎' + 𝑏'𝑖) = (𝑎 - 𝑎') + (𝑏 - 𝑏') 𝑖.

Разностью двух комплексных чисел может быть комплексное, действительное и чисто мнимое число.

Примеры. (1 - 𝑖) - (2 - 3𝑖) = - 1 + 2𝑖; (4 + 5𝑖) - (2 + 5𝑖) = 2 + 0𝑖 = 2; (9 -8𝑖) - (9 + 8𝑖) = -16𝑖.

Умножение. Произведением комплексных чисел 𝑎 + 𝑏𝑖 и 𝑎' + 𝑏'𝑖 называется комплексное число

(𝑎𝑎' - 𝑏𝑏') + (𝑎𝑏' + 𝑏𝑎') 𝑖.

Отсюда следует, что для умножения комплексных чисел достаточно перемножить их как алгебраические двучлены и в полученном результате заменить 𝑖² = -1.

Произведение сопряженных чисел (Произведение двух несопряженных комплексных чисел тоже может быть действительным числом; например (2 + 3𝑖)(4 - 6𝑖) = 26. Если же и сумма, и произведение двух комплексных чисел являются действительными числами, то эти комплексные числа непременно сопряженные) 𝑎 + 𝑏𝑖 и 𝑎 - 𝑏𝑖 есть вещественное число, равное 𝑎² + 𝑏².

Пример. (2 + 𝑖)(2 - 𝑖) = 4 - 𝑖² = 5.

Умножение комплексных чисел подчиняется тем же основным законам, что и умножение действительных чисел.

Деление. Деление комплексных чисел можно определить, как действие, обратное умножению. Отсюда следует, что частное от деления комплексного числа 𝑎 + 𝑏𝑖 на число 𝑎' + 𝑏'𝑖 равно

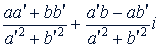
Практически удобнее всего деление комплексных чисел проводить следующим образом: сначала умножить делимое и делитель на число, сопряженное делителю, после чего делитель станет действительным положительным числом, а затем провести деление действительной и мнимой частей отдельно.

Пример.

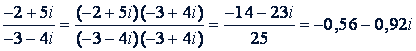
Возведение в степень. Предварительно найдем результаты от возведения в степень мнимой единицы 𝑖, зная что 𝑖² - 1.

𝑖¹ = 𝑖; 𝑖³ = - 𝑖; 𝑖⁵ = 𝑖; 𝑖⁷ = - 𝑖;

𝑖² = - 1; 𝑖⁴ = 1; 𝑖⁶ = -1; 𝑖⁸ = 1.

Мы получили, таким образом, четыре чередующихся значения:

𝑖^4𝑘 = +1; 𝑖^4𝑘+1 = 𝑖; 𝑖^4𝑘+2 = -1; 𝑖^4𝑘+3 = - 𝑖,

где

𝑘 = 0, ±1, ±2 и т.д.

Следует иметь в виду, что 𝑖 ⁰ принимается равным 1.

Возведение комплексного числа в целую степень производится так:

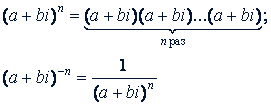
Здесь 𝑛 - натуральное число. Умножение можно проводить последовательно. Кроме того, принимается (𝑎 + 𝑏𝑖)⁰ = 1.

Извлечение квадратного корня. Извлечение корня из комплексного числа есть действие, обратное возведению в степень, посредством которого по данной степени (подкоренное число) и данному показателю степени (показатель корня) находят основание (корень). В множестве комплексных чисел действие извлечения корня всегда выполнимо, и в результате получается столько значений, каков показатель корня. В частности, квадратный корень имеет два значения, которые находят по формуле

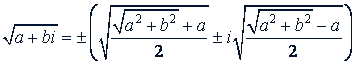
где знак "+" в скобках берется при 𝑏 > 0, а знак "-" - при 𝑏 < 0.

Пример.

3. Геометрическое изображение комплексных чисел. Известно, что действительные числа можно изображать точками на прямой. Комплексные числа 𝑧 = 𝑎 + 𝑏𝑖 взаимно однозначно сопоставляются с парами действительных чисел (𝑎, 𝑏). Поэтому комплексное число 𝑧 = 𝑎 + 𝑏𝑖 условились геометрически изображать точкой 𝑀, у которой в прямоугольной системе координат абсцисса равна 𝑎, а ордината 𝑏 (рис. 72).

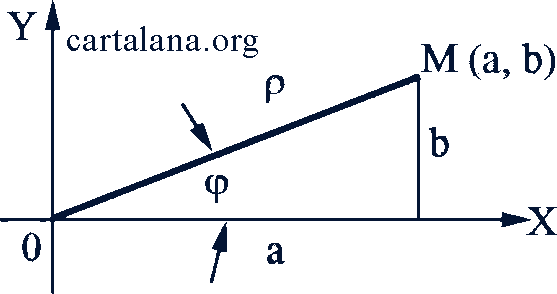
Рис. 72

Комплексное число можно также изображать направленным отрезком (вектором) 𝑂𝑀, т.е. отрезком прямой, у которого указано, какая из ограничивающих его точек является началом и какая концом. В нашем случае 𝑂 есть начало, а 𝑀 - конец. Значит, комплексное число 𝑧 = 𝑎 + 𝑏𝑖 изображают вектором, начало которого совпадает с началом координат, а конец - с точкой 𝑀. Сам вектор обозначают 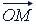; направление вектора указывает стрелка на его конце.

Длина вектора, изображающего комплексное число, называется модулем этого комплексного числа. Модуль всякого комплексного числа, не равного нулю, есть положительное число. Модуль комплексного числа 𝑎 + 𝑏𝑖 обозначают |𝑎 + 𝑏𝑖| а также буквой 𝑟. Из чертежа (рис. 72) видно, что

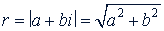
Модуль действительного числа совпадает с его абсолютным значением. Сопряженные комплексные числа 𝑎 + 𝑏𝑖 и 𝑎 - 𝑏𝑖 имеют один и тот же модуль.

Примеры.

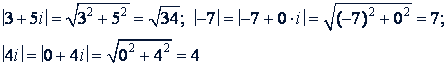
Угол φ между положительным направлением оси абсцисс и вектором 𝑂𝑀, изображающим комплексное число 𝑎 + 𝑏𝑖, называется аргументом комплексного числа 𝑎 + 𝑏𝑖. Каждое комплексное число, не равное нулю, имеет бесконечное множество аргументов, отличающихся друг от друга на целое число оборотов (т.е. на 360° 𝑘, где 𝑘 - любое целое число) (Для комплексного числа 𝑧 = 0 аргумент теряет смысл).

Аргумент φ комплексного числа 𝑎 + 𝑏𝑖 связан с 𝑎 и 𝑏 следующими формулами:

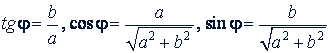
Однако ни одна из них в отдельности не позволяет найти аргумент по абсциссе и ординате. Покажем это на примерах.

Пример. Найти аргумент комплексного числа -3 -3i.

Решение. Первый способ. 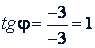. Этому условию удовлетворяют как угол 45°, так и угол 225°. Но угол 45° не является аргументом числа -3 -3𝑖 (рис. 73). Правильный ответ будет φ = 225° (или -135°, или 585° и т.д.). Этот результат получится, если учесть, что абсцисса и ордината данного комплексного числа отрицательны. Значит, точка 𝑀 лежит в третьей четверти.

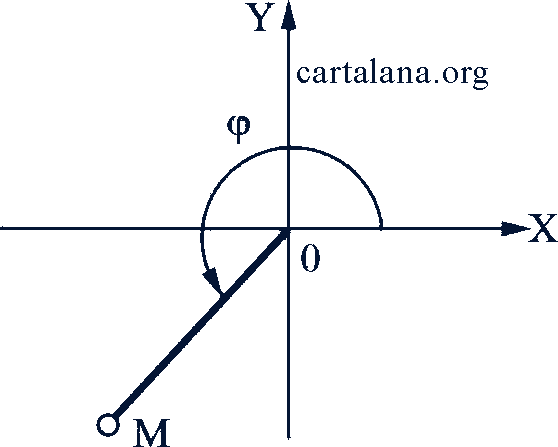
Рис. 73

Второй способ. 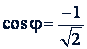. Формула для sin φ показывает, что он тоже отрицателен. Значит, угол φ принадлежит третьей четверти, так что φ = 225° ±360° 𝑘.

Наименьшее по абсолютной величине значение аргумента называется главным. Так, для комплексного числа -3 -3𝑖 главное значение аргумента равно -135°.

Аргумент действительного положительного числа имеет главное значение 0°; для отрицательных чисел главным значением аргумента принято считать 180° (а не -180°).

У сопряженных комплексных чисел главные значения аргумента имеют одни и те же абсолютные значения, но противоположные знаки. Так, главные значения аргумента чисел -3 + 3𝑖 и -3 -3𝑖 равны соответственно 135° и -135°.

Для обозначения аргумента 𝑧 = 𝑎 + 𝑏𝑖 приняты обозначения φ = Arg 𝑧, или φ = arg 𝑧. Первое употребляется для всевозможных значений аргумента; второе - для главного значения аргумента, выделяемого неравенством 0 ≤ φ ≤ 2π

46. Тригонометрическая форма комплексного числа

1. Определения. Общая форма записи комплексного числа, т.е. форма 𝑎 + 𝑏𝑖, называется алгебраической. Абсцисса 𝑎 и ордината 𝑏 комплексного числа 𝑎 + 𝑏𝑖 выражаются через модуль 𝑟 и аргумент φ (рис. 73) формулами

𝑎 = 𝑟 cos φ, 𝑏 = 𝑟 sin φ.

Тогда получим:

𝑎 + 𝑏𝑖 = 𝑟 (cos φ + 𝑖 sin φ).

Последнее выражение называется тригонометрической формой комплексного числа с модулем 𝑟 и аргументом φ. Любое число 𝑧 ≠ 0 может быть представлено в тригонометрической форме.

Пример 1. Представить в тригонометрической форме число -3 + 2𝑖.

Решение.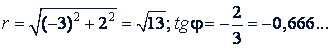

Тангенс отрицателен, следовательно, значение φ надо искать во второй и четвертой четвертях. Обращаясь к формулам для sin φ и cos φ, замечаем, что при 𝑎 = -3 и 𝑏 = 2 синус будет положителен, а косинус отрицателен, что имеет место во второй четверти (Удобнее четверть определять по знакам при 𝑎 и 𝑏. В данном случае 𝑎 = -3, 𝑏 = +2. Точку с такими координатами находят во второй четверти). По таблицам находим φ = 146° 18', значит .

Пример 2. Представить в тригонометрической форме число 1 - 𝑖.

Решение. Имеем: 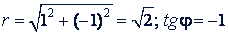. Здесь 𝑎 = 1, а 𝑏 = -1. Следовательно, φ находится в четвертой четверти. Отсюда находим φ = 315° и можем написать:

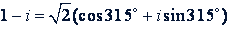
Примечание. Так как 315° = 360° - 45° и cos 315° = cos 45°; sin 315° = sin (-45°) = -sin 45°, то это число можно записать и так:

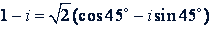
Пример 3. Представить в тригонометрической форме действительное число 𝑚 > 0.

Решение. Так как 𝑚 = 𝑚 + 0 · 𝑖, то 𝑎 = 𝑚, 𝑏 = 0, и тогда

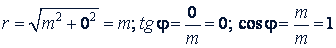
Следовательно, φ = 0 и можно написать:

𝑚 = 𝑚 (cos 0° + 𝑖 sin 0°)

или в общем виде

𝑚 = 𝑚 (cos 360° 𝑘 + 𝑖 sin 360° 𝑘).

Отсюда делаем вывод, что модулем положительного числа является само это число, а аргументом его есть 0° (или 360° 𝑘).

Пример 4. Представить в тригонометрической форме отрицательное число - 𝑚 (𝑚 > 0).

Решение. Так как - 𝑚 = - 𝑚 + 0 · 𝑖, то 𝑎 = - 𝑚, 𝑏 = 0, и мы имеем: 𝑟 = 𝑚, tg φ = 0, cos φ = -1. Следовательно, φ = 180°, и тогда

- 𝑚 = 𝑚 (cos 180° + 𝑖 sin 180°),

или в общем виде:

- 𝑚 = 𝑚 [cos (180° + 360° 𝑘) + 𝑖 sin (180° + 360° 𝑘)] = 𝑚 [cos 180° (2𝑘 + 1) + 𝑖 sin 180° (2𝑘 + 1)].

Следовательно, модулем отрицательного числа является его абсолютная величина, а аргумент равен 180°, или в общем виде 180°(2𝑘 + 1).

Пример 5. Выразить в алгебраической форме число

4(cos 30° + 𝑖 sin 30°).

Решение. Так как

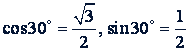
то имеем:

Далее рассмотрим, как выполнять действия над комплексными числами, заданными в тригонометрической форме.

Сложение и вычитание комплексных чисел проще и удобнее проводить, когда они даны в алгебраической форме. Для остальных алгебраических действий более удобна тригонометрическая форма.

⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨

МЕНЮ САЙТА / СОДЕРЖАНИЕ