Я создала и активно наполняю телеграм-канал "Перець". Здесь лучшие карикатуры из журнала, начиная с 1922 года.
Заходите, подписывайтесь: https://t.me/cartalana

ШВЕЦОВ К.И., БЕВЗ Г.П."СПРАВОЧНИК ПО ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ. АРИФМЕТИКА, АЛГЕБРА", 1965

МЕНЮ САЙТА / СОДЕРЖАНИЕ

2. Задачи на геометрическую прогрессию.

Задача 1. Вычислить пятый член геометрической прогрессии, в которой первый член равен 3, а знаменатель прогрессии 2.

Решение. 𝑢₁ = 3, 𝑞 - 2; 𝑢 ₅ = 𝑢₁𝑞^5-1 = 3 · 24 = 48.

Ответ. 𝑢 ₅ = 48.

Задача 2. Найти сумму членов геометрической прогрессии, в которой .

Решение.

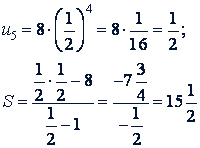
Ответ.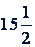

Задача 3. Определить первый член и сумму членов геометрической прогрессии, в которой

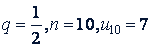
Решение.

𝑢_𝑛 = 𝑢₁ 𝑞^{𝑛 -1}, 𝑢₁₀ = 𝑢₁ 𝑞⁹

Отсюда

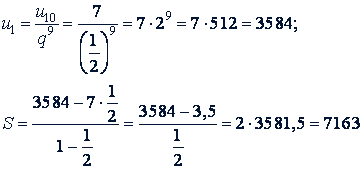
Ответ. 3584, 7163.

Задача 4. Определить первый и последний члены геометрической прогрессии, в которой

𝑛 = 8, 𝑞 = 2, 𝑆₈ = 765.

Решение. Используя формулы общего члена и суммы прогрессии, получаем:

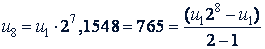
или

𝑢₈ = 𝑢₁ · 128, 765 = 𝑢₁(2⁸ - 1).

Решив эти уравнения относительно 𝑢₁ и 𝑢₈, получим:

𝑢₁ = 3, 𝑢_𝑛 = 384.

Ответ. 3; 384.

Задача 5. Найти геометрическую прогрессию, состоящую из 6 членов, зная, что сумма трех первых ее членов равна 168, а сумма трех последних 21.

Решение.

𝑎₁ + 𝑎₂ + 𝑎₃ = 168;

𝑎₄ + 𝑎₅ + 𝑎₆ = 21,

или

𝑎 + 𝑎𝑞 + 𝑎𝑞² = 168;

𝑎𝑞³ + 𝑎⁴ + 𝑎𝑞⁵ = 21.

Отсюда

𝑎(1+ 𝑞 + 𝑞²) = 168;

𝑎𝑞³(1 + 𝑞 + 𝑞²) = 21.

Значит, 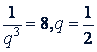. Тогда 𝑎 = 96.

Ответ. 96, 48, 24, 12, 6, 3.

Задача 6. Найти три числа, образующие возрастающую геометрическую прогрессию, зная, что их сумма равна 26, сумма квадратов этих чисел 364.

Решение. Так как 𝑎₁ 𝑎 ₂, 𝑎 ₃ образуют геометрическую прогрессию, то 𝑎₁ = 𝑎, 𝑎 ₂ = 𝑎𝑞, 𝑎 ₃ = 𝑎𝑞². Тогда по условию имеем:

𝑎 + 𝑎𝑞 + 𝑎𝑞² = 26,

𝑎² + 𝑎² 𝑞² + 𝑎² 𝑞⁴ = 364.

Решив систему, получим: 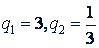и 𝑎 = 2. Так как прогрессия возрастающая, то ее знаменатель будет 3.

Ответ. 2, 6, 18.

Задача 7. Три положительных числа, дающие в сумме 21, составляют арифметическую прогрессию. Если к ним соответственно прибавить 2, 3 и 9, то полученные числа составят геометрическую прогрессию. Найти эти числа.

Решение.

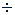𝑎, 𝑎 + 𝑑, 𝑎 + 2𝑑.

∺ 𝑎 + 2, 𝑎 + 𝑑 + 3, 𝑎 + 2𝑑 + 9.

Согласно условию, имеем:

𝑎 + 𝑎 + 𝑑 + 𝑎 + 2𝑑 = 21,

или

3𝑎 + 3𝑑 = 21,

или

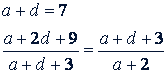
После преобразований получим:

𝑑² + 2𝑑 - 5𝑎 - 9 = 0.

Так как 𝑎 = 7 - 𝑑, то 𝑑² + 7𝑑 - 44 = 0; 𝑑₁ = 4, 𝑑 ₂ = -11. Тогда 𝑎₁ = 3, 𝑎 ₂ = 18.

Второе значение не удовлетворяет условию задачи, так как оно приводит к числам 18, 7 и -4, а последнее из них неположительное. Следовательно, 𝑑 = 4 и 𝑎 = 3. Тогда имеем такие числа: 3, 7, 11.

Ответ. 3, 7, 11.

Задача 8. Найти сумму бесконечно убывающей геометрической прогрессии

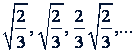
Решение.

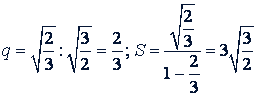
Ответ.

Задача 9. Сумма бесконечно убывающей геометрической прогрессии равна 12,5, а сумма первого и второго членов ее 12. Найти эту прогрессию.

Решение. По условию, 𝑆 = 12,5; 𝑢₁ + 𝑢 ₂ - 12. Имеем: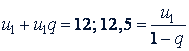

Исключив из этой системы 𝑢₁ получим квадратное уравнение

12,5𝑞² - 0,5 = 0.

Тогда или 𝑢₁ = 15.

Ответ. ∺ 10; 2; 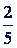; … и

∺ 15; -3; ; …

3. Исторические сведения о прогрессиях. Прогрессии встречаются уже у математиков глубокой древности - в папирусе Ахмеса, у Архимеда, у некоторых китайских математиков. Древние индийские математики также знали арифметическую и геометрическую прогрессии, а Брахмагупта (628 г. н.э.) рассматривал, кроме того, последовательности, построенные из квадратов и кубов чисел натурального ряда.

Само слово "прогрессия" было введено римскими математиками, его употреблял, в частности, Боециус (510 г. н.э.).

Старые математики связывали между собой понятия "пропорции" и "прогрессии". Прилагая к пропорциям наименования арифметической, геометрической и гармонической, они считали, что пропорция является ничем иным, как четырехчленной прогрессией. Большинство из них давало лишь формулу суммы прогрессии, причем без доказательства; некоторые приводили также формулу для определения последнего члена арифметической прогрессии, также без доказательства. Правило для нахождения любого члена арифметической прогрессии было дано Карданом в 1539 г.

Формула для суммы членов геометрической прогрессии впервые в западноевропейской литературе встречается в книге Фибоначчи (1202 г.), затем ее приводит Пойербах (1460 г.). Формула эта для суммирования бесконечной прогрессии была обобщена французским математиком Виетом в 1590 г.

44. Метод математической индукции

Во многих разделах современной математики используется метод доказательства, который называется методом математической индукции. В его основе лежит следующая аксиома индукции. Если некоторое утверждение справедливо для 𝑛 = 1 и если из допущения справедливости его для какого-нибудь произвольного натурального 𝑛 = 𝑘 следует справедливость его и для 𝑛 = 𝑘 + 1, то это утверждение справедливо для всякого натурального 𝑛.

Пример 1. Доказать формулу общего члена арифметической прогрессии:

𝑎_𝑛 = 𝑎₁ + (𝑛 - 1) 𝑑.

Доказательство. Она верна для 𝑛 = 1, так как тогда будет 𝑎₁ = 𝑎₁. Предположим, что формула верна для 𝑛 = 𝑘, т.е. 𝑎_𝑘 = 𝑎₁ + (𝑘 - 1) 𝑑. Тогда 𝑎_{𝑘 +1} = 𝑎_𝑘 + 𝑑 = 𝑎₁ + (𝑘 - 1) 𝑑 + 𝑑 = 𝑎₁ + 𝑘𝑒.

Как видим, если формула верна для 𝑛 = 𝑘, то она верна и для 𝑛 = 𝑘 + 1. Для 𝑛 = 1 она верна. Следовательно, доказываемая формула верна при каждом натуральном значении 𝑛.

Пример 2. Доказать, что при любом 𝑛

1 + 3 + 5 +... + (2𝑛 - 1) =².

Доказательство. При 𝑛 = 1 это равенство верно: 1 = 1.

Предположим, что оно верно при некотором произвольном 𝑛 = 𝑘, т.е., что

1 + 3 + 5 +... + (2𝑘 - 1) = 𝑘².

Тогда, прибавив к обеим его частям одно и тоже число 2𝑘 + 1, получим

1 + 3 + 5 +... + (2𝑘 - 1) + (2𝑘 + 1) = 𝑘² + 2𝑘 + 1,

или

1 + 3 + 5 +... + (2𝑘 - 1) + [2(𝑘 + 1) - 1] = (𝑘 + 1)².

Итак, рассматриваемое равенство справедливо при 𝑛 = 1, и из допущения справедливости его при 𝑛 = 𝑘 вытекает, что оно справедливо и при 𝑛 = 𝑘 + 1. Следовательно, оно верно при каждом натуральном 𝑛.

Методом математической индукции можно доказывать и такие утверждения, которые при 𝑛 = 1 не верны, но которые верны, начиная с некоторого натурального 𝑝, большего 1. При этом используют такое следствие из аксиомы индукции: если некоторое утверждение справедливо для 𝑛 = 𝑝 и если из допущения справедливости его для какого-нибудь 𝑛 - 𝑘 ≥ 𝑝 вытекает справедливость его и для 𝑛 = 𝑘 + 1, то это утверждение справедливо для всех натуральных чисел, начиная с 𝑝.

Пример 3. Доказать, что при всех 𝑛 ≥ 5 имеет место неравенство

2ⁿ > 𝑛².

Доказательство. При 𝑛 = 5 это неравенство верно, так как 32 > 25.

Предположим, что при некотором произвольном 𝑘 ≥ 5

2^𝑘 > 𝑘²

тогда должно быть верным также неравенство

2^𝑘 + 2^𝑘 > 𝑘² + 𝑘².

Но так как 2^𝑘 + 2^𝑘 = 2^{𝑘 +1} и при 𝑘 ≥ 5𝑘² > 2𝑘 + 1, то из предположения следует

2^{𝑘 +1} > 𝑘² + 2𝑘 + 1,

или

2^𝑘 > (𝑘 + 1)².

Как видим, если данное неравенство верно при 𝑛 = 𝑘 ≥ 5, то оно верно и при 𝑛 = 𝑘 + 1. При 𝑛 = 5 оно верно. Следовательно, это неравенство справедливо при всех натуральных 𝑛 ≥ 5.

КОМПЛЕКСНЫЕ ЧИСЛА И УРАВНЕНИЯ ВЫСШИХ СТЕПЕНЕЙ

45. Комплексные числа

1. Определения. В множестве действительных чисел не всякое уравнение степени выше первой имеет решение. Так, например, уравнение 𝑥² + 1 = 0 не имеет действительных корней, поскольку не существует действительного числа, квадрат которого равен числу -1. Это привело к расширению множества действительных чисел путем введения чисел новой природы. Эти новые числа называют мнимыми.

Число, удовлетворяющее равенству 𝑥² = -1, обозначают буквой 𝑖, оно называется мнимой единицей (Существуют два различных мнимых числа, удовлетворяющих равенству 𝑥² = -1. Мнимой единицей называют только одно из них. Его обозначают символом 𝑖. Второе число, удовлетворяющее этому же равенству, обозначают символом - 𝑖 и называют числом, сопряженным к мнимой единице). Таким образом, 𝑖² = -1.

Число 𝑧 = 𝑎 + 𝑏𝑖, где 𝑎 и 𝑏 - любые действительные числа; 𝑖 - мнимая единица, называется комплексным числом. Числа 𝑎 и 𝑏𝑖 называются соответственно действительной и мнимой частями комплексного числа 2.

При 𝑎 = 0 комплексное число 𝑎 + 𝑏𝑖 обращается в чисто мнимое число 𝑏𝑖; при 𝑏 = 0 получим число 𝑎 + 0𝑖, т.е. действительное число 𝑎.

Таким образом, множество комплексных чисел включает в себя и все действительные числа. Каждое известное нам число, например 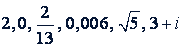, 𝑖 можно назвать комплексным числом. На схеме показано, как связаны между собой различные виды чисел.

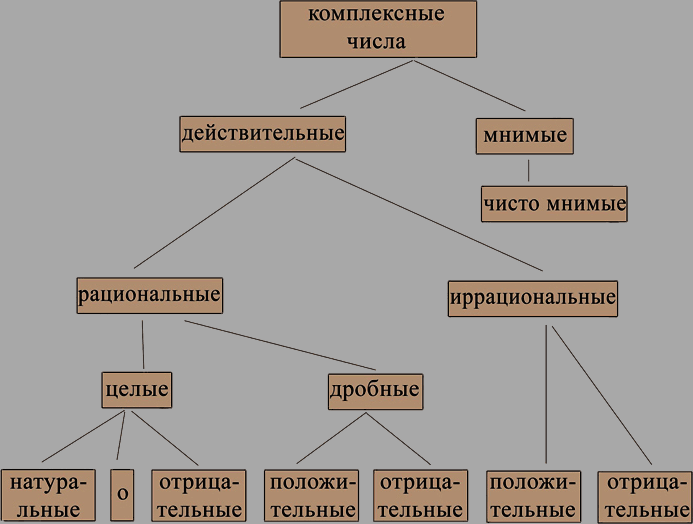
Комплексные числа вида 𝑎 + 𝑏𝑖 и 𝑎 -𝑏𝑖 называются сопряженными. Комплексные числа вида 𝑎 + 𝑏𝑖 и -𝑎 - 𝑏𝑖 называются противоположными.

Два комплексных числа 𝑎 + 𝑏𝑖 и 𝑎' + 𝑏'𝑖 считаются равными в том и только в том случае, если

𝑎 = 𝑎', 𝑏 = 𝑏'.

Из этого определения вытекает, что комплексное число 𝑎 + 𝑏𝑖 равно нулю тогда и только тогда, когда 𝑎 = 0 и 𝑏 = 0.

⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨

МЕНЮ САЙТА / СОДЕРЖАНИЕ