Я создала и активно наполняю телеграм-канал "Перець". Здесь лучшие карикатуры из журнала, начиная с 1922 года.
Заходите, подписывайтесь: https://t.me/cartalana
ШВЕЦОВ К.И., БЕВЗ Г.П."СПРАВОЧНИК ПО ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ. АРИФМЕТИКА, АЛГЕБРА", 1965
8. Освобождение подкоренного выражения от дроби. Используя два предыдущих преобразования радикалов, можно освобождать подкоренные выражения от дроби.
Примеры. Освободить подкоренные выражения от дроби:
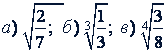
Решение.
а) Чтобы в первом радикале из знаменателя можно было извлечь квадратный корень, умножим оба члена дроби на 7:
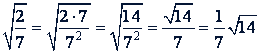
б) Чтобы во втором радикале из знаменателя можно было извлечь кубический корень, умножим оба члена дроби на 3²:
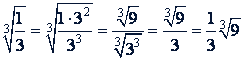
в) Чтобы в третьем радикале из знаменателя можно было извлечь корень четвертой степени, умножим оба числа на 2 (так как 8 = 2³):
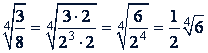
Если подкоренное выражение - алгебраическая дробь, подобные примеры решают аналогично.
Примеры.
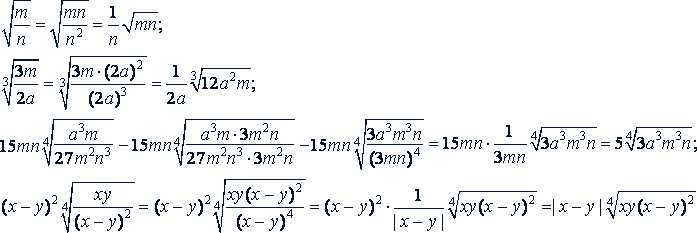
Примечание. Последние примеры можно решать и другим способом:
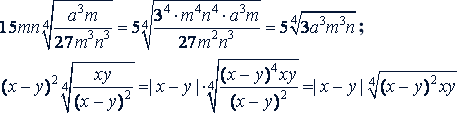
9. Приведение радикалов к простейшему виду. Для того чтобы привести радикал к простейшему, или нормальному виду, надо выполнить последовательно такие операции:
1) упростить подкоренное выражение (если это возможно);
2) сократить показатели корня и подкоренного выражения (если они имеют общий множитель);
3) вынести из-под радикала рациональные множители;
4) освободить подкоренное выражение от дроби.
Примеры. Привести к простейшему виду следующие радикалы:
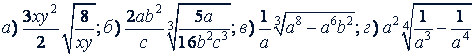
Решение.
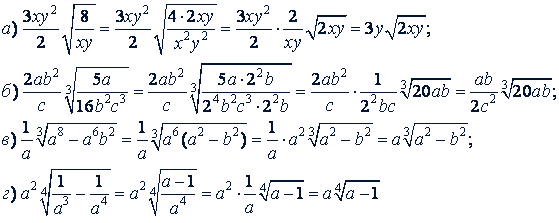
10. Подобие радикалов. Два или несколько радикалов называются подобными, если они одинаковой степени и имеют одинаковые подкоренные выражения.
Пример.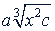 
и 
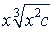- подобные радикалы, так как они оба третьей степени и имеют одинаковые подкоренные выражения 𝑖² 𝑐. Иногда данные радикалы оказываются подобными только после некоторых преобразований.
Примеры.
а) Подобны ли радикалы
?
Решение.
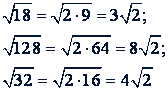
Ответ. Подобны.
б) Подобны ли радикалы
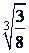и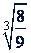 
Решение.
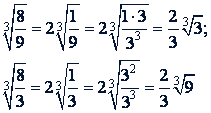
Ответ. He подобны.
в) Подобны ли радикалы
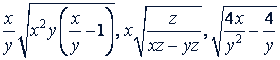
Решение.
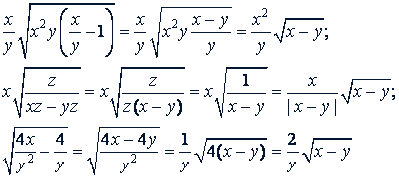
Ответ. Подобны.
1. Сложение и вычитание. Чтобы сложить (или вычесть) радикалы, их соединяют знаками плюс (или минус) и приводят подобные члены, если они окажутся.
Примеры. Выполнить указанные действия:
а) 
.
Решение.
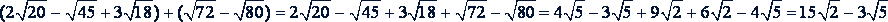
б)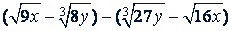 
Решение.
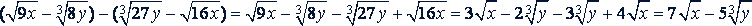
в)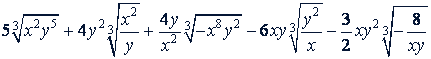 
Решение.
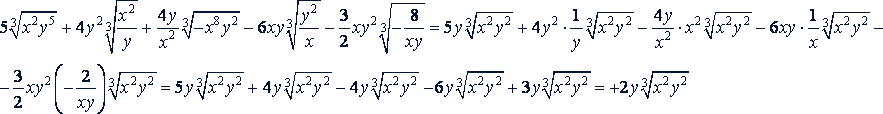
г)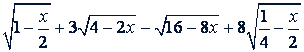 
Решение.
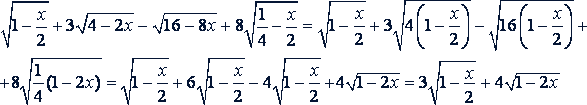
2. Умножение. Чтобы перемножить несколько радикалов одинаковой степени, надо перемножить подкоренные выражения и из произведения извлечь корень той же степени.
Если перемножаются радикалы с различными показателями, то их надо предварительно привести к одному показателю. Если перед радикалами имеются коэффициенты, то их перемножают.
Пример 1. Выполнить умножение:
а)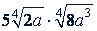 
.
Решение.
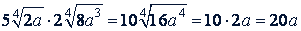
б)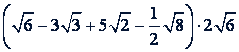 
Решение.
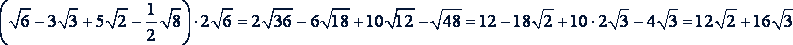
в)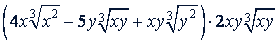 
Решение.
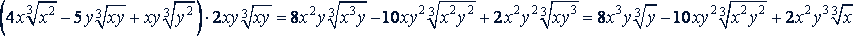
г)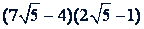 
Решение.
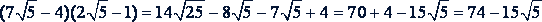
Пример 2. Перемножить радикалы с различными показателями:
а)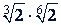 
.
Решение.
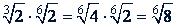
б)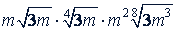 
.
Решение.
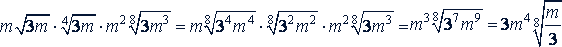
в)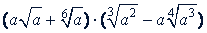 
Решение.
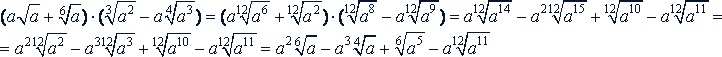
3. Деление. Чтобы разделить радикалы с одинаковыми показателями, надо разделить их подкоренные выражения и из частного извлечь корень той же степени.
Чтобы разделить радикалы с различными показателями, их надо привести предварительно к одинаковым показателям. Если есть коэффициенты, то их делят.
Пример 1. Выполнить деление:
а)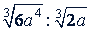 
.
Решение.
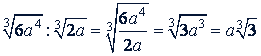
б)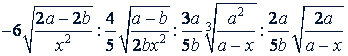 
Решение.
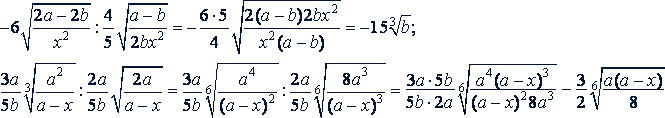
в)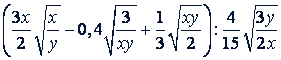 
Решение.
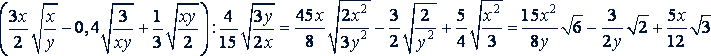
г)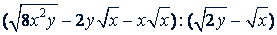 
Решение.
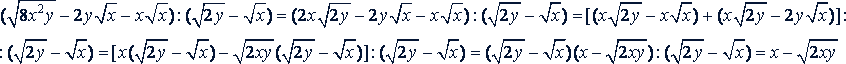
Пример 2. Выполнить деление с помощью формул сокращенного умножения:
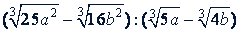
Решение.
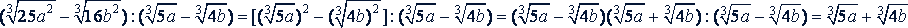
4. Возвышение в степень. Чтобы возвысить радикал в степень, надо возвысить в эту степень подкоренное выражение, оставив тот же показатель корня:
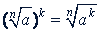
Примеры.
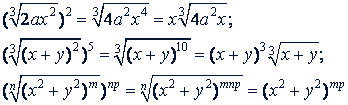
Алгебраические суммы радикалов можно возводить в степень, пользуясь формулами сокращенного умножения.
Примеры.
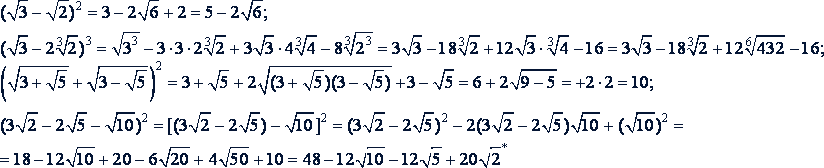
(Можно также воспользоваться формулой квадрата многочлена)
5. Извлечение корня. Чтобы извлечь корень из корня, надо перемножить показатели корней:
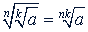
Примеры.
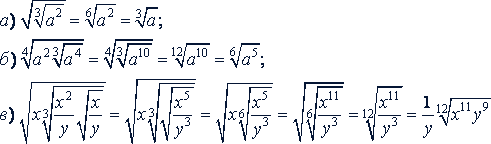
6. Квадратный корень из двучлена вида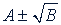 
. При преобразовании выражений, содержащих квадратные радикалы, иногда пользуются формулой
,
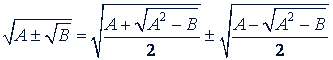где 𝑎 > 0, 𝑏 > 0 и 𝑎² > 𝑏, а знаки в правой и левой части одновременно берутся либо верхние, либо нижние (соответственно). Эта формула называется формулой сложного радикала.
Примеры.
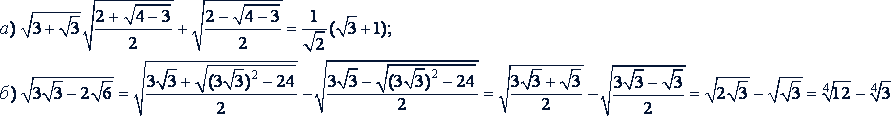
7. Уничтожение иррациональности в знаменателе или числителе дроби. Замена дроби, у которой знаменатель (числитель) - иррациональное выражение, тождественной ей дробью с рациональным знаменателем (числителем) называется уничтожением иррациональности в знаменателе (числителе) дроби.
Ниже рассмотрены основные приемы уничтожения иррациональностей в знаменателях. Уничтожение иррациональностей в числителях дробей выполняется аналогично.
а) Дробь вида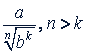 
. В этом случае умножают числитель и знаменатель на такой множитель, чтобы в знаменателе корень извлекался бы нацело, т.е. на 
.
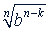Примеры.
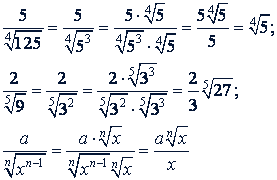
б) Дробь вида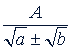 
. Числитель и знаменатель умножают на сопряженное (Сопряженным множителем относительно иррационального выражения 𝑀 называется всякое выражение 𝐵, неравное тождественно нулю, такое, что произведение 𝑀𝐵 не содержит радикалов) выражение 
.
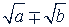В частном случае, когда дробь вида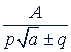 
, то ее члены умножают на 
.
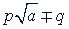Примеры.
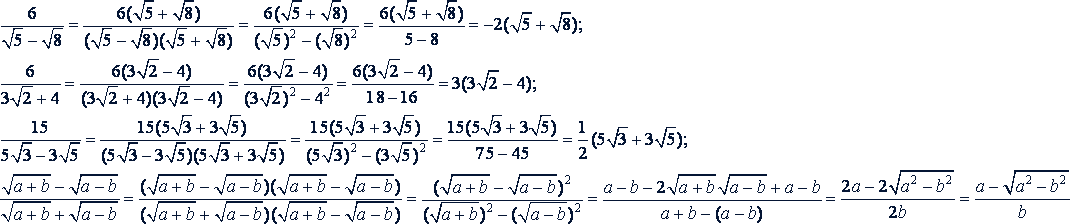
в) Дробь вида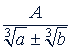 
. В этом случае числитель и знаменатель дроби умножают на неполный квадрат разности или суммы: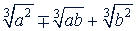 
Примеры.
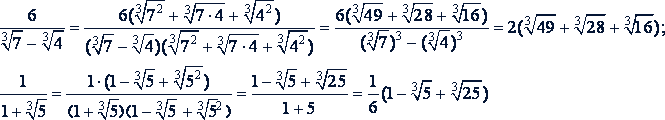
г) Дробь вида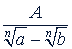 
. В этом случае сопряженный множитель определяется на основании тождества
𝑎𝑛 - 𝑏𝑛 = (𝑎 - 𝑏)(𝑎𝑛-1 + 𝑎𝑛-2𝑏 +...+ 𝑏𝑛-1)
Для дроби вида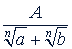 
сопряженный множитель определяется на основании тождества
𝑎𝑛 + 𝑏𝑛 = (𝑎 + 𝑏)(𝑎𝑛-1 - 𝑎𝑛-2 +... ±𝑏𝑛-1
(последний член 𝑏𝑛-1 берется со знаком + при 𝑛 нечетном, и – при 𝑛 четном).
Пример.
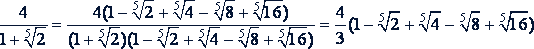
Если в знаменателе встречаются радикалы с разными показателями, то надо предварительно привести их к одному знаменателю.
Пример.
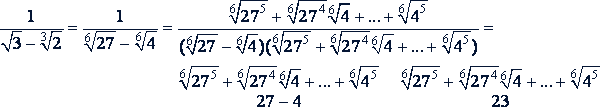
Но такие примеры можно решать и другим способом, уничтожая сначала один радикал, а затем второй:
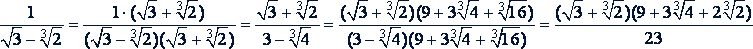
д) Дробь вида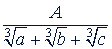 
. В этом случае пользуются тождеством
(𝑎 + 𝑏 + 𝑐)(𝑎² + 𝑏² + 𝑐² - 𝑎𝑏 - 𝑏𝑐 - 𝑎𝑐) = 𝑎³ + 𝑏³ + 𝑐³ - 3𝑎𝑏𝑐
е) Если в знаменателе имеются три и более радикалов, то иногда полезно предварительно сгруппировать члены и свести данный случай к уже разобранным.
Пример.
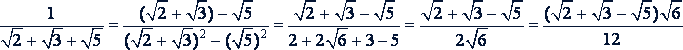
8. Примеры более сложных преобразований
а) Доказать, что при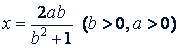 
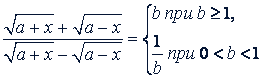
Доказательство.
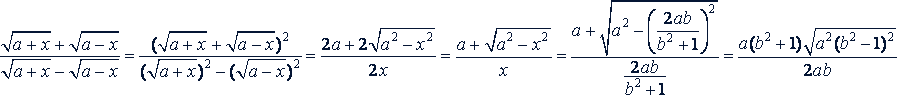
Если 0< 𝑏 < 1 и 𝑎 > 0, то
.
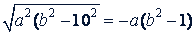Следовательно, данное выражение равно
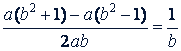
Если 𝑏 ≥то данное выражение равно
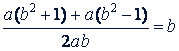
б) Доказать, что если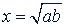 
и 𝑎 > 𝑏 > 0, то
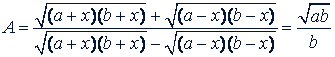
Решение. Разделив числитель и знаменатель на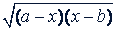 
, получим:
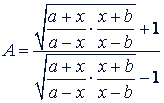
Так как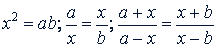 
и 𝑎 > 𝑏 > 0, то 
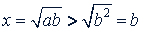, т.е. 𝑥 > 𝑏 > 0, и
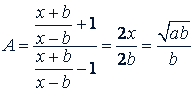
Примечание. Этот и следующий примеры можно также решить, непосредственно подставляя вместо 𝑥 его значение.
в) Найти
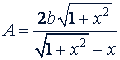
при
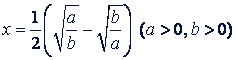
Решение.
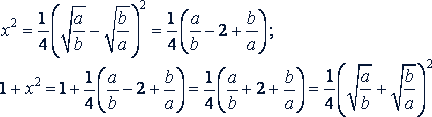
Подставим значение 𝑖 и 1 + 𝑖² в данное выражение
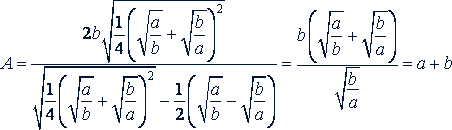
г) Упростить выражение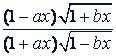 
при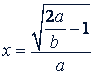 
, если 𝑎 < 𝑏 < 2𝑎.
Решение. Из условия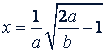 
следует 
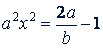или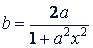 
Поэтому
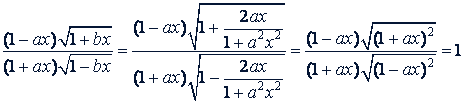
так как при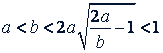 
, следовательно 1 - 𝑎𝑥 > 0 и 1 + 𝑎𝑥 > 0.
д) Преобразовать
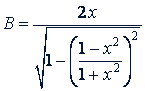
где 𝑥 - любое действительное число, отличное от нуля.
Решение.
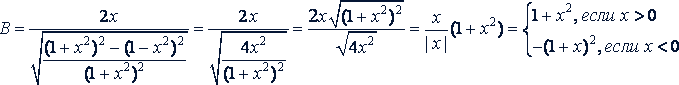
⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨
МЕНЮ САЙТА / СОДЕРЖАНИЕ