
Я создала и активно наполняю телеграм-канал "Перець". Здесь лучшие карикатуры из журнала, начиная с 1922 года.
Заходите, подписывайтесь: https://t.me/cartalana

ШВЕЦОВ К.И., БЕВЗ Г.П."СПРАВОЧНИК ПО ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ. АРИФМЕТИКА, АЛГЕБРА", 1965
1. Понятие арифметического действия. Если по двум данным числам определяют третье число, удовлетворяющее некоторым условиям, то этот процесс в математике вообще называют действием.
В арифметике рассматривают следующие действия: сложение, вычитание, умножение и деление называют арифметическими действиями.
2. Сложение. Сложением натуральных чисел называют арифметическое действие, при помощи которого узнают число, содержащее столько единиц, сколько их есть в данных числах вместе.
Числа, которые нужно сложить, называют слагаемыми, а результат сложения, т.е. число, получающееся от сложения, называют суммой.
Например: 11 + 9 = 20. Здесь 11 и 9 - слагаемые, 20 - сумма. Знак сложения + (плюс) ставится между слагаемыми.
Однозначные (Однозначными, двузначными и т.д. называют числа, записанные одной, двумя и т.д. цифрами. Число, записанное несколькими цифрами, называют также многозначным) числа складывают, пользуясь таблицей сложения:
1 + 1 = 2,
2 + 1 = 3 и т.д.
Эту таблицу дети запоминают еще в первом классе.
Сложение многозначных чисел удобней выполнять "в столбик", записывая слагаемые числа так, чтобы единицы были против единиц, десятки против десятков и т.д., например
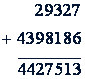
Сложение натуральных чисел всегда возможно и однозначно, т.е., какие бы числа в качестве слагаемых ни брали, всегда можно найти их сумму и эта сумма должна быть для каждых данных чисел одна и та же.
Прибавление к числу нуля не изменяет этого числа, например 12 + 0 = 12; 0 + 12 = 12; 0 + 0 = 0.
Примечание. Древнейшим приемом сложения целых чисел было сложение слева направо; результат записывался сверху. Джон Голивуд (Сакробоско) ввел сложение справа налево; впоследствии этот прием распространился по всей Европе. Знак сложения + (плюс) возник не ранее XV в. По-видимому, он образовался путем стилизации латинского союза "et" (и). Тогда же появился и термин "сумма" в смысле результата сложения.
В России вместо "сложение" в XVII-XVIII вв. иногда применялся латинский термин "аддиция".
3. Вычитание. Вычитанием называется действие, посредством которого по данной сумме и одному данному слагаемому отыскивается другое слагаемое. Таким образом, число, которое при сложении является искомым, при вычитании оказывается данным, и наоборот. Поэтому вычитание называют действием, обратным сложению.
Число, из которого вычитают, называется уменьшаемым. Число, которое вычитают, - вычитаемым. Число, которое получается в результате вычитания, называется разностью.
Пример. 30 - 12 = 18. Здесь 30 - уменьшаемое, 12 - вычитаемое, а 18 - разность. Знак вычитания минус (-) ставится между уменьшаемым и вычитаемым.
Вычитание в множестве натуральных чисел выполнимо лишь при условии, когда уменьшаемое больше вычитаемого. При этом разность выражается всегда определенным единственным натуральным числом.
Примечания:
а) Вычитание нуля из числа не изменяет этого числа, например, 8 - 0 = 8.
б) Если уменьшаемое равно вычитаемому, то разность равна нулю. Например, 9 - 9 = 0.
Подобно сложению более старым является прием, при котором вычитание ведется слева направо. Прием этот применялся в Западной Европе почти до XV в. Знак минус (—) появился в учебниках арифметики в XV в. одновременно со знаком плюс (+). Латинское название действия вычитания ("субстракцио") применялось и в России в начале XVIII в.
4. Умножение. Умножением натуральных чисел называется действие, состоящее в нахождении суммы одинаковых слагаемых. Например, если число 5 нужно повторить слагаемым 7 раз, то пишут: 5 × 7 = 35, и говорят, что нужно 5 умножить на 7:
5 + 5 + 5 + 5 + 5 + 5 + 5 = 5 × 7.
Можно сказать иначе: умножить одно натуральнoe число на другое - значит взять первое число слагаемым столько раз, сколько единиц во втором числе. При этом то число, которое повторяется как слагаемое, называется множимым, число, показывающее, сколько берется таких одинаковых слагаемых, - множителем, а число, полученное в результате умножения - произведением. Так, в нашем примере, 5 - множимое, 7 - множитель, 35 - произведение. Множимое и множитель называются также сомножителями.
Знак умножения (×) ставится между множимым и множителем. В качестве знака умножения часто употребляется точка (·), например 3 · 5 = 15. (Перед буквенными сомножителями знак умножения не ставят)
Примечания:
а) Если один из двух сомножителей равен единице, то произведение равно второму сомножителю, например
1 · 5 = 5; 10 · 1 = 10.
б) Если хоть один сомножитель равен нулю, то и произведение равно нулю:
0 · 342 = 0; 37 · 0 = 0; 0 · 0 = 0.
5. Исторические сведения об умножении натуральных чисел. В древней Индии умножение начинали с высших разрядов, т.е. слева направо. Способ умножения справа налево был выработан, по-видимому, не раньше XV в.
Знак умножения (×) был предложен в первой половине XVII в. Точка, как знак умножения, появилась в XV в. Название действия, принятое в большинстве европейских языков и встречающееся также у старых русских авторов, "мультипликацио" применялось еще в древнем Риме.
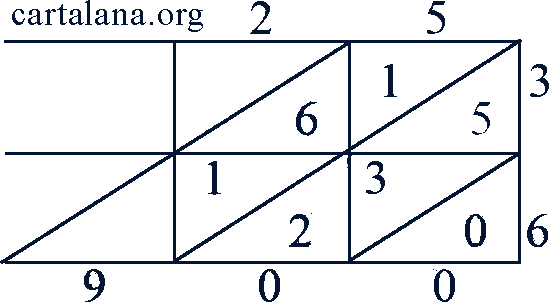
Среднеазиатскими учеными был разработан способ умножения решеткой, который применялся также и в Западной Европе. Например, при умножении числа 25 на 36 эти числа записывали около сторон прямоугольника, который делился горизонтальными и вертикальными чертами на несколько частей (в зависимости от числа разрядов). Полученные меньшие прямоугольники делились пополам диагоналями, идущими снизу вверх направо. Результат поразрядного умножения записывался внутри маленьких прямоугольников, начиная с нижнего ряда так, что высший разряд стоял над диагональю, а низший - под ней. Умножаем сначала 25 на 6 и произведение записываем в нижнем ряду прямоугольника: 5 · 6 = 30, нуль пишем в нижнем правом прямоугольнике под диагональю, а 3 над ней; 2 · 6 = 12; 2 записываем во втором справа нижнем прямоугольнике под диагональю (т.е. в разряде десятков), а 1 - над диагональю (в разряде сотен). Затем умножаем 25 на 3 и аналогично записываем произведение в верхнем ряду, после чего соответствующие разряды, складываем по диагоналям:
Интересный также древнерусский способ умножения. При умножении этим способом один из сомножителей последовательно делим пополам (остаток отбрасывается), а второй удваиваем. Потом складываем числа второй последовательности, соответствующие нечетным числам первой последовательности.
Пример.
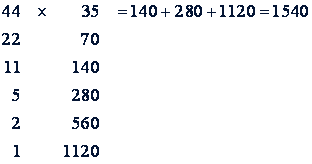
Древнерусский способ умножения применяется сейчас на счетных машинах. Оказывается, что умножение этим способом на некоторых машинах выполняется в 2-2,5 раза быстрее, чем умножение на тех же машинах способом последовательного сложения (П.Г. Xоменко, Умножение на счетных машинах, Машгиз, М., 1962).
6. Деление. Делением называется действие, посредством которого по данному произведению двух сомножителей и одному из этих сомножителей отыскивается другой сомножитель.
Число, которое делят, называется делимым; число на которое делят, - делителем; число, которое получается в результате деления, называется частным, или отношением.
Деление записывается так: 40 : 8 = 5. Здесь 40 - делимое, 8 - делитель, а 5 - частное. Знак деления: (двоеточие) ставится между делимым и делителем.
Число, которое при умножении является искомым, при делении оказывается данным, и наоборот. Поэтому деление называется действием, обратным умножению.
Примечания:
а) Если делимое равно делителю, то частное равно единице, например 14 : 14 = 1.
б) Если делитель равен единице, то частное равно делимому, например 14 : 1 = 14.
в) Частное от деления нуля на какое-либо число, отличное от нуля, равно нулю, например 0 : 12 = 0.
г) Деление на нуль невозможно.
Деление натуральных чисел не всегда выполнимо. Например, нельзя разделить 30 на 7, ибо нет такого натурального числа, которое при умножении на 7 давало бы 30.
7. Деление с остатком. Как видим, разделить 30 на 7 (в указанном выше смысле) невозможно. Но в жизни встречаются ситуации, которые требуют распространить деление натуральных чисел и на такие случаи, например, разделить 30 тетрадей между 7 учениками поровну.
Поэтому рассматривают также деление с остатком.
Примечание. Чтобы не смешивать деление с остатком с рассмотренным выше арифметическим действием делением, последнее называют еще делением без остатка или делением нацело.
Деление с остатком - есть отыскание наибольшего целого числа, которое в произведении с делителем дает число, не превышающее делимое. Искомое число называется неполным частным. Разность между делимым и произведением делителя на неполное частное называется остатком; он всегда меньше делителя.
Пример. 19 не делится нацело на 5. Числа 1, 2, 3 при умножении на 5 дают 5, 10, 15, не превосходящие делимого 19, но уже 4 дает в произведении с 5 число 20, большее 19. Поэтому неполное частное будет 3, а остаток - 4 (разность между 19 и произведением 3 · 5 = 15); 19 = 5 · 3 + 4.
Для натуральных чисел точному делению (делению без остатка) и делению с остатком можно дать следующее общее определение: разделить число 𝑎 (делимое) на число 𝑏 (делитель) - значит найти такие два числа 𝑞 (частное) и 𝑟 (остаток), которые удовлетворяли бы соотношениям:
𝑎 = 𝑏𝑞 + 𝑟, 0 ≤ 𝑟 < 𝑏.
Если делитель 𝑏 не равен нулю, то деление всегда возможно и дает единственный результат.
Остатком при делении на число 𝑏 может быть любое из чисел 0, 1, 2, ... 𝑏 - 1.
Примечание. В древности деление считалось самым трудным действием, которым мог овладеть не каждый. Причиной этого был очень громоздкий прием деления, который был занесен в Западную Европу вместе с арабскими учебниками и применялся до XVIII в. Способ, который является в настоящее время общепринятым, был разработан итальянскими учеными в XV в. Название действия, общепринятое в западноевропейских языках и применявшееся в России вплоть до первой половины XVIII в., - "дивизио", заимствовано из латинского языка. Знак деления (:) был принят в XVII в.
8. Возведение в степень. Частный случай умножения, а именно умножение одинаковых чисел, называют возведением в степень. Если, например, надо перемножить 5 одинаковых чисел, каждое из которых равно 2, говорят: надо число возвести в пятую степень. И вместо 2 · 2 · 2 · 2 · 2 пишут 25.
Возвести число во вторую, третью, четвертую и т.д. степень значит взять его сомножителем соответственно два, три, четыре и т.д. раза. Число, повторяющееся сомножителем, называется основанием степени; число, указывающее, сколько раз берется одинаковый множитель, называется показателем степени, а результат - степенью.
Запись: 53 = 5 · 5 · 5 = 125; здесь 5 - основание степени, 3 - показатель степени, 125 - степень.
Вторая степень называется иначе квадратом, третья степень - кубом. Первой степенью числа называют само это число, например 71 = 7.
⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨
МЕНЮ САЙТА / СОДЕРЖАНИЕ