
Я создала и активно наполняю телеграм-канал "Перець". Здесь лучшие карикатуры из журнала, начиная с 1922 года.
Заходите, подписывайтесь: https://t.me/cartalana

ШВЕЦОВ К.И., БЕВЗ Г.П."СПРАВОЧНИК ПО ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ. АРИФМЕТИКА, АЛГЕБРА", 1965
Арифметика - наука о числах. Название "арифметика" произошло от греческого слова αριθμητιχη, состоящего из двух частей: απιθμος - число и θεχνη - искусство. Арифметика, как и многие другие науки, возникла из потребностей практической деятельности людей. Еще задолго до нашей эры у людей возникла необходимость подсчитывать количество добычи, вести счет времени и т.п. Несомненно, что сначала люди оперировали только конкретными именованными числами, и только позже начали употреблять абстрактные числа.
Сначала людям были известны только натуральные числа, но позже жизнь заставила расширить понятие числа, рассматривать и дробные числа. Когда впервые появилось понятие дроби, не известно. Но исследования показывают, что древние египтяне, китайцы, хорезмийцы за много веков до нашей эры были знакомы с дробными числами и умели выполнять простейшие арифметические действия над ними.
В арифметике как науке рассматриваются все виды чисел от натуральных до комплексных. Однако в школьной арифметике изучают только положительные рациональные числа, а остальные виды чисел рассматриваются в алгебре. Авторы данного справочника придерживаются школьных традиций. В "Справочнике" отрицательные, иррациональные и мнимые числа изложены в главе "Алгебра", а в главе "Арифметика" рассматриваются только натуральные и дробные числа.
Первые книги, содержащие учение о счете и вычислениях, появились еще за несколько веков до нашей эры. Много арифметических сведений есть в "Началах" Евклида (III в. до н.э.), в "Арифметике" Диофанта (III в н.э.) и других книгах древнегреческих математиков.
Известный хорезмский математик Мухаммед ибн Муса (около 780-850 гг.), использовав известные ему работы греческих и индийских математиков, написал книгу по арифметике, которая в латинском переводе попала в Европу в XII в. и содействовала распространению десятичной позиционной нумерации.
В Киевской Руси были широко распространены элементарные сведения из области арифметики, включая действия с обыкновенными дробями, что доказывается наличием косвенных источников. От XVII вв. сохранились рукописи математического содержания, из анализа которых явствует, что познания в арифметике на Руси того времени соответствовали уровню, достигнутому в Западной Европе. В начале XVIII в. появляются и печатные учебники по арифметике. Так, в 1703 г. была издана "Арифметика" Л.Ф. Магницкого, самая популярная книга на протяжении первой половины XVIII в., которую М.В. Ломоносов называл "вратами своей учености". Этот учебник энциклопедического содержания, кроме арифметики, включал элементы геометрии и технических наук. В 1740 г. было напечатано "Руководство к арифметике" Л. Эйлера. Во второй половине XVIII в. вышли из печати учебники арифметики, написанные академиками С.К. Котельниковым, С.Я. Румовским и другими авторами. Широко распространены были в то время "Универсальная арифметика" Н.Г. Курганова, а также "Теоретическая и практическая арифметика" профессора Московского университета Д.С. Аничкова.
В 1866 г. были изданы "Руководство арифметики" и "Собрание арифметических задач" А.Ф. Малинина и К.П. Буренина, по которым учились в русских средних школах на протяжении полустолетия. Во второй половине XIX в. вышли в свет учебники по арифметике Ф.И. Симашко, В.А. Латышева, В.А. Евтушевского и других авторов. В 1884 г. издана "Арифметика" А.П. Киселева, на которой воспиталось несколько поколений русских, а затем и советских специалистов и которую только недавно заменил учебник "Арифметика" И.Н. Шевченко.
1. Натуральный ряд чисел.Когда пересчитывают какие-нибудь предметы, называют в строго определенном порядке числа: один, два, три, четыре, пять, шесть и т.д. Изображают их символами
1, 2, 3, 4, 5, 6, ...
Эти числа называют натуральными. Множество натуральных чисел, упорядоченных в строго определенной указанной выше последовательности, называют натуральным рядом чисел, или короче натуральным рядом.
То из двух натуральных чисел, которое в натуральном ряде ближе стоит к 1, т.е. которое при счете появляется раньше, называется меньшим, второе число - большим (Приведенные описания нельзя считать строгими определениями. Строгие определения этих понятий очень сложны (см. "Энциклопедия элементарной математики", Гостехиздат, М., 1951, стр. 133, 142 и др.)). Следовательно, в натуральном ряде каждое число, кроме 1, больше предыдущего. 1 - наименьшее натуральное число, но наибольшего натурального числа нет. Какое бы ни было большое натуральное число, существует еще большее следующее за ним натуральное число. Натуральный ряд бесконечен. Это показал еще в III в. до н.э. древнегреческий математик Архимед.
Таблица 1. Устная нумерация некоторых народов
| Число 1 2 3 4 5 6 7 8 9 10 20 30 40 50 60 70 80 90 100 1000 | Болгарская един два три четири пет шест седем осем девет десет двадесет тридесет четиридесет петдесет шестдесет седемдесет осемдесет деветдесет сто хиляда | Польская jeden dwa trzy cztery pieć sześć siedem osiem dziewięć dziesięć dwadzieścia trzydzieścia czterdzieści piećdziesiąt szescdziesiąt siedemdziesiąt osiemdziesiąt dziewięćdziesiąt sto tysiąc | Чешская jeden dva tři čtyři pět šest sedm osm devět deset dvacet třicet čtyřicet padesat šedesát sedmdesát osmdesát dévadesat sto tisic | Сербохорватская jedan dva tri četiri pet šest sedam osam devet deset dvadeset trideset četrdeset pedeset šezdeset sedamdeset osamdeset devedeset sto tisuća | Латышская viens divi trīs četri pieci seši septiņi astoņi deviņi desmit divdesmit trīsdesmit četrdesmit piecdesmit sešdesmit septiņdesmit astoņdesmit deviņdesmit simts tūkstotis |
| Число 1 2 3 4 5 6 7 8 9 10 20 30 40 50 60 70 80 90 100 1000 | Латинская unus duo tres quattuor quinque sex septem octo novem decern viginti triginta quadraginta quinquaginta sexaginta septuaginta octoginta nonaginta centum mille | Английская one two three four five six seven eight nine ten twenty thirty fourty fifty sixty seventy eighty ninety hundred thousand | Немецкая ein zwei drei vier fünf sechs sieben acht neun zehn zwanzig dreizig vierzig funfzig sechzig siebzig achtzig neunzig hundert Tausend | Французская un deux trois quatre cinq six sept huit neuf dix vingt trente quarante cinquante soixante soixante-dix quatre-vingt quatre-vingt-dix cent mille | Испанская uno dos tres сuatro cinco seis siete ocho nueve diez veinte treinte сuarenta cincuenta sesenta setenta ochenta noventa cien mil |
2. Устная нумерация. При помощи слов "один", "два", "три", "четыре", "пять", "шесть", "семь", "восемь", "девять", "десять", "сорок", "сто", "тысяча", "миллион", "миллиард", определенным способом комбинируя их, можно назвать очень большие числа, встречающиеся в практике.
Устная нумерация у большинства народов появилась очень давно. О большом сходстве названий чисел у разных европейских народов см. табл. 1.
3. Письменная нумерация. Для записи натуральных чисел используют символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Их называют цифрами. С помощью этих десяти цифр можно записать любое натуральное число.
Пример. 327 - триста двадцать семь, 1002 - тысяча два.
Такая экономная запись чисел достигается благодаря применению принципа поместного значения цифр. В зависимости от занимаемого цифрой места она может обозначать то одно, то другое число. Так, в приведенном выше примере цифра 2 в первом случае обозначает двадцать, а во втором - два.
Первая, вторая, третья и т.д. цифры числа, если считать справа налево, называются соответственно цифрами единиц, десятков, сотен и т.д. Их называют еще единицами первого, второго, третьего и т.д. разрядов. Например, в числе 7194 имеется 4 единицы первого, 9 единиц второго, 1 единица третьего и 7 единиц четвертого разрядов. Цифрой "0" - нуль обозначают отсутствие единиц того или иного разряда. Десять единиц какого-нибудь разряда составляют одну единицу следующего высшего разряда. Поэтому говорят, что мы пользуемся десятинной системой счисления.
Десятичная система счисления возникла в глубокой древности. Люди стали пользоваться ею потому, что привыкли считать десятками, имея на руках десять пальцев. Однако некоторые народы в свое время создали и недесятичные системы счисления.
Принцип поместного значения цифр и начертания цифр (правда, несколько отличные от современных) возникли в Индии только в начале н.э. В Европе они стали известны благодаря книге "Арифметика Индорум", которую написал хорезмский математик Мухаммед ибн Муса. Она была написана на арабском языке и поэтому стали называть эти цифры арабскими. Позже, узнав, что Мухаммед в основу имеющейся в книге нумерации положил практику вычислителей Индии, стали называть эти цифры индийскими.
В России с индийской нумерацией познакомились только в XIII в. До этого числа обозначали старославянскими буквами, только сверху писали специальные значки  (титло):
(титло):
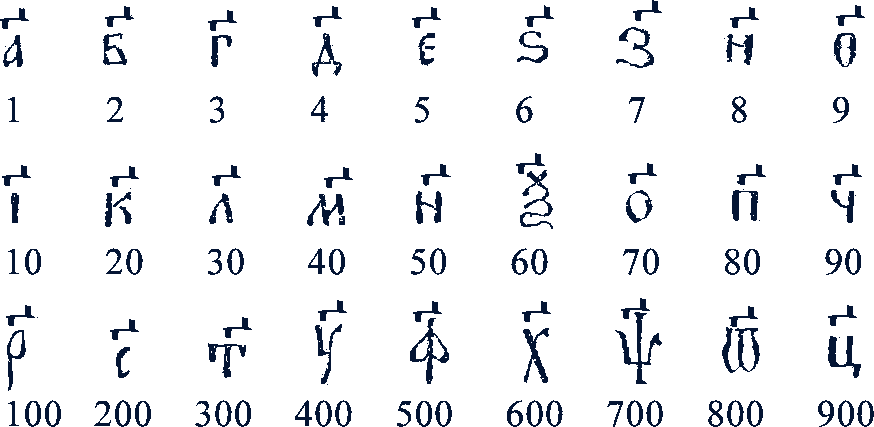
Тысячи обозначали теми же буквами, но впереди ставили значок ![]() . Например, числа 7205, 1963 записывали соответственно так:
. Например, числа 7205, 1963 записывали соответственно так:

В некоторых случаях еще и сейчас пользуются римскими цифрами. Римская система нумерации состоит из семи знаков:
1 - I, 5 - V, 10 - X, 50 - L, 100 - С, 500 - D, 1000 - М
При этом, если меньший знак пишется после большего, то его прибавляют к большему числу; если же перед большим - вычитают, например: 8 - VIII, 24 - XXIV, 26 - XXVI, 46 - XLVI, 176 - CLXXVI, 1963 - MCMLXIII.
4. Целые числа. О нуле мы уже упоминали, но рассматривали его только как цифру (знак), а не число. Однако в математике принято рассматривать нуль не только как цифру, но и как число.
0 - число не натуральное. Нуль меньше 1 и любого натурального числа. Если разместить нуль и все натуральные числа в порядке возрастания, получим:
0, 1, 2, 3, 4, 5, 6, ...
Эту последовательность чисел называет расширенным натуральным рядом.
Все натуральные числа и нуль называются вместе целыми неотрицательными числами. Но так как в арифметике обычно отрицательных чисел не рассматривают, здесь их называют просто целыми числами (В алгебре целыми числами называют все натуральные числа, нуль и все целые отрицательные числа: -1, -2, -3 и т.д.).
5. Названия больших чисел. Для удобства чтения и запоминания больших чисел их цифры разбивают на классы: справа отделяют три цифры - первый класс, следующие три - второй класс и т.д. Последний класс может иметь три, две или одну цифру. Между классами обычно оставляют небольшие промежутки. Например, в числе 2365423 первый класс дает число единиц, второй - число тысяч и третий - число миллионов. Сообразно с этим записанное число читают так: два миллиона триста шестьдесят пять тысяч четыреста двадцать три.
Единицы четвертого, пятого, шестого и т.д. классов называют соответственно:
миллиард или биллион - 1 000 000 000,
триллион - 1 000 000 000 000,
квадриллион - 1 000 000 000 000 000,
квинтиллион - 1 000 000 000 000 000 000,
секстиллион - 1 000 000 000 000 000 000 000,
септиллион - 1 000 000 000 000 000 000 000 000.
Эти названия возникли сравнительно недавно. Существующее сейчас в большинстве европейских языков выражение "миллион" - 106 возникло в Италии в XIII в. (106 = 1000000. Вообще 10𝑛 обозначает число, записанное единицей с 𝑛 последующими нулями) Термины "биллион", "миллиард" и т.п. возникли в XVI-XVII вв., но до сих пор имеют различное (в разных языках) значение. Миллиард обычно означает 109, но то же значение имеет в США и во Франции биллион, тогда как в Германии биллион означает 1012. Триллион в США и во Франции означает 1012, а в Англии и Германии - 1018. В русских математических рукописях встречаются наименования больших чисел, возникших, по-видимому, не раньше XII в.: тьма - 106, легион - 1012, леодр - 1024, ворон - 1048, колода - 1049.
⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨
МЕНЮ САЙТА / СОДЕРЖАНИЕ