Я создала и активно наполняю телеграм-канал "Перець". Здесь лучшие карикатуры из журнала, начиная с 1922 года.
Заходите, подписывайтесь: https://t.me/cartalana
ЧЕРТОВ А.Г. "ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН", 1977
Удельная газовая постоянная. Удельной газовой постоянной В вещества называют величину, равную отношению молярной газовой постоянной R к молярной массе М данного вещества:
B = R/M. (8.7)
В отличие от молярной газовой постоянной, удельная газовая постоянная имеет разные значения для различных веществ.
Из формулы (8.7) следует, что единица удельной газовой постоянной
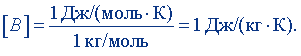
Джоуль на килограмм-кельвин равен удельной газовой постоянной идеального газа массой 1 кг, совершающего при повышении температуры на 1 К и постоянном давлении работу 1 Дж.
Согласно формуле (8.7), размерность удельной газовой постоянной:
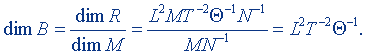
Единицу и размерность удельной газовой постоянной можно найти также по формуле
В = А/mΔТ, (8.8)
где А - работа, совершаемая газом при изобарическом нагревании на интервал температур ΔT, m - масса газа.
Градиент плотности. Быстроту изменения плотности среды в некотором направлении х характеризуют величиной, называемой градиентом плотности и выражаемой формулой
grad ρ = dρ/dx·i, (8.9)
где i - единичный вектор оси х. В случае равномерного изменения плотности можно записать
grad ρ = Δρ/Δx·i. (8.10)
Подставив сюда Δρ = 1 кг/м3, Δx = 1 м, i = |i| = 1, получим единицу градиента плотности:
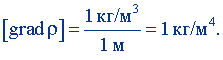
Килограмм на метр в четвертой степени равен градиенту плотности среды, плотность которой на участке длиной 1 м в направлении градиента изменяется на 1 кг/м3. Размерность градиента плотности:
dim grad ρ = L-4M.
Коэффициент диффузии. Коэффициент диффузии определяется из формулы
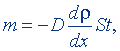(8.11)
где m - масса газа, перенесенного за время t через площадку S, dρ/dx - градиент плотности. Отсюда получим
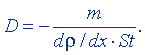(8.12)
Положив m = 1 кг, S = 1 м2, t = 1 с, dρ/dx = 1 кг/м4, найдем единицу коэффициента диффузии:
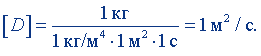
Квадратный метр в секунду равен коэффициенту диффузии среды, в которой через площадку в 1 м2 перпендикулярно градиенту плотности, равному 1 кг/м4, переносится в 1 с вещество массой 1 кг.
Для определения единицы коэффициента диффузии можно воспользоваться формулой
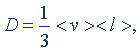(8.13)
где <v> - средняя скорость хаотического движения молекул, <l> - средняя длина свободного пробега молекул. Чтобы единица коэффициента диффузии оказалась в этом случае когерентной, формулу (8.13) пришлось бы брать с числовым коэффициентом, равным единице:
[D] = [v][l].
Положив здесь v = 1 м/с, l = 1 м, найдем
[D] = 1 м/с · 1 м = 1 м2/с.
Как из формулы (8.12), так и из (8.13) следует, что размерность коэффициента диффузии:
dim D = L2T-1.
Динамическая вязкость (коэффициент вязкости, коэффициент внутреннего трения). Динамическая вязкость была определена и получена ее единица на основе гидродинамической формулы (7.39). Теперь получим эту единицу с помощью формулы молекулярной физики.
При рассмотрении вязкости, как явления переноса, на основе молекулярно-кинетической теории выведена следующая формула динамической вязкости:
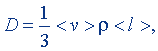(8.14)
ρ - плотность газа. Для получения когерентной единицы динамической вязкости образуем по (8.14) формулу
[η] = [v][ρ][l]. (8.15)
Положив здесь v = 1 м/с, ρ = 1 кг/м3, l = 1 м, найдем [η] = 1 м/с · 1 кг/м3 · 1 м = 1 кг·м/(с·м2) = 1 кг·м·с/(с2·м2) = 1 Н·с/м2.
Как указано выше, эта единица называется паскаль-секунда. Там же дано ее определение.
Из формулы (8.15) найдем размерность динамической вязкости:
dim η = L-1MT-1,
что совпадает с размерностью, полученной по формуле (7.39).
Градиент температуры (температурный градиент). Если температура Т среды в некотором направлении х изменяется, то быстроту ее изменения характеризуют величиной, называемой градиентом температуры:
grad T = dT/dx·i,
где i - единичный вектор оси х.
Градиент температуры - величина векторная. Совокупность векторов градиента температуры образует температурное поле.
В случае равномерного изменения температуры в направлении градиента можно записать
grad Т = ΔТ/Δх·i. (8.16)
Подставив ΔТ = 1 К, Δx = 1 м, i = |i| = 1, получим единицу градиента температуры:
[grad T] = 1 К/1 м = 1 К/м.
Кельвин на метр равен температурному градиенту поля, в котором на участке длиной 1 м в направлении градиента температура изменяется на 1 К. Размерность градиента температуры:
dim grad T = L-1Θ.
Температурный коэффициент давления газа. Температурный коэффициент β давления газа - величина, равная отношению относительного изменения давления газа к изменению его температуры:
β = dp/(p0dT).
Если в некотором интервале ΔT температур температурный коэффициент β давления газа остается постоянным, то
β = Δр/(р0ΔТ), (8.17)
где р0 - начальное давление газа, Δр - изменение его давления при изменении температуры на ΔT.
Подставив в (8.17) Δр = р0, ΔT = 1 К, получим
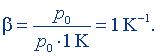
Эту единицу называют кельвин в минус первой степени. Кельвин в минус первой степени равен температурному коэффициенту относительного изменения физической величины, при котором изменение температуры на 1 К от принятой за начальную вызывает относительное изменение этой величины, равное единице. Размерность температурного коэффициента давления:
dim β = Θ-1.
Температурный коэффициент линейного расширения. Температурный коэффициент α линейного расширения есть величина, равная отношению относительного удлинения dl/l0 тела к изменению dT температуры, вызвавшему это удлинение, т.е.
α = dl/(l0dT).
Если коэффициент линейного расширения в интервале ΔT постоянен, то
α = Δl/(l0ΔT). (8.18)
Подставив здесь Δl = l0, ΔТ = 1 К, получим
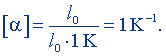
Размерность коэффициента линейного расширения:
dim α = Θ-1.
Температурный коэффициент объемного расширения. Температурный коэффициент объемного расширения β есть величина, равная отношению относительного увеличения объема dV/V0 тела к изменению dT температуры, вызвавшему это увеличение объема:
β = dV/(V0dT).
Если коэффициент объемного расширения в интервале ΔT постоянен, то
β = ΔV/(V0ΔT). (8.19)
Положив в этой формуле ΔV = V0, ΔТ = 1 К, найдем
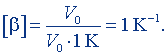
Размерность коэффициента объемного расширения:
dim β = Θ-1.
Внутренняя энергия. Внутренней энергией U называют энергию, зависящую только от термодинамического состояния системы. Внутренняя энергия состоит из кинетической энергии хаотического движения молекул, атомов, свободных электронов и других микрочастиц, потенциальной энергии взаимодействия этих частиц, внутриатомной и внутриядерной энергии частиц, составляющих систему.
Внутренняя энергия идеального газа состоит только из кинетической энергии его молекул.
Единицу внутренней энергии найдем из первого начала термодинамики для адиабатического процесса, при котором система совершает работу А против внешних сил только за счет убыли своей внутренней энергии ΔU:
А = -ΔU. (8.20)
Из равенства (8.20) следует, что внутренняя энергия выражается в тех же единицах, что и работа, т.е. в джоулях. Размерность внутренней энергии:
dim U = dim A = L2MT-2.
Количество теплоты (теплота). Количество теплоты * - это внутренняя энергия, которая самопроизвольно (без внешнего воздействия) переходит от тел более нагретых к телам менее нагретым путем теплопроводности или лучеиспускания.
* Такой термин рекомендован Государственным стандартом "Единицы физических величин". Более удачным является термин "теплота". Применение этого термина привело бы к большему единообразию в терминологии, использованной в стандарте, так как в нем имеются термины "теплота фазового превращения", "теплота химической реакции" и др.
Единица количества теплоты может быть получена из равенства, выражающего первое начало термодинамики для изотермического процесса:
Q = A, (8.21)
где Q - количество теплоты, полученное системой, А - работа, совершаемая системой при изменении объема.
Из (8.21) следует, что количество теплоты выражается в тех же единицах, что и работа, т.е. в джоулях. Размерность количества теплоты:
dim Q = L2MT-2.
В джоулях выражается также теплота фазового превращения и теплота химической реакции.
Удельное количество теплоты. Удельным количеством теплоты q называют величину, равную отношению количества теплоты Q, полученного (или переданного) системой, к массе m системы:
q = Q/m. (8.22)
Положив Q = 1 Дж, m = 1 кг, получим единицу удельного количества теплоты:
[q] = 1 Дж/1 кг = 1 Дж/кг.
Джоуль на килограмм равен удельному количеству теплоты системы, в которой веществу массой 1 кг сообщается (или отбирается от него) количество теплоты 1 Дж. Размерность удельного количества теплоты:
dim q = L2T-2.
В джоулях на килограмм выражается также удельная теплота фазового превращения и химической реакции. Приведем формулы, по которым определяются единицы удельной теплоты соответственно парообразования, плавления, сгорания:
r = Q/m, (8.23)
где Q - количество теплоты, необходимое для превращения в пар той же температуры жидкости массой m;
λ = Q/m, (8.24)
где Q - количество теплоты, необходимое для расплавления кристаллического вещества массой m, взятого при температуре плавления;
q = Q/m, (8.25)
где Q - количество теплоты, выделяющееся при полном сгорании топлива массой m.
Теплоемкость системы. Теплоемкость С тела (системы тел) - величина, равная отношению количества теплоты
Q, необходимой для нагревания тела (системы тел), к разности ΔT температур тела, т.е.
C = Q/ΔT. (8.26)
Положив в (8.26) Q = 1 Дж, ΔT = 1 К, получим единицу теплоемкости:
[С] = 1 Дж/1К = 1 Дж/К.
Джоуль на кельвин равен теплоемкости системы, температура которой повышается на 1 К при подведении к системе количества теплоты 1 Дж. Размерность теплоемкости:
dim C = L2MT-2Θ-1.
Удельная теплоемкость. Удельной теплоемкостью с вещества называют величину, равную отношению теплоемкости однородного тела к его массе, т.е.
с = С/m,
или с учетом (8.26)
c = Q/(mΔТ). (8.27)
Положив m = 1 кг, Q = 1 Дж, ΔТ = 1 К, получим единицу удельной теплоемкости:
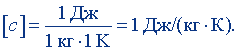
Джоуль на килограмм-кельвин равен удельной теплоемкости вещества, имеющего при массе 1 кг теплоемкость 1 Дж/К. Размерность удельной теплоемкости:
dim c = L2T-2Θ-1.
⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨
МЕНЮ САЙТА / СОДЕРЖАНИЕ