Я создала и активно наполняю телеграм-канал "Перець". Здесь лучшие карикатуры из журнала, начиная с 1922 года.
Заходите, подписывайтесь: https://t.me/cartalana
ЧЕРТОВ А.Г. "ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН", 1977
Коэффициент Пуассона. При продольном растяжении образца происходит уменьшение его поперечных размеров, которое характеризуется абсолютным Δd и относительным Δd/d сжатиями, где d - поперечный размер образца. Отношение относительного сжатия к относительному удлинению называют коэффициентом Пуассона μ:
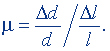(7.30)
Так как Δd/d и Δl/l - величины безразмерные, то и коэффициент Пуассона - величина безразмерная и, следовательно, выражается в безразмерных единицах.
Модуль сдвига. Модулем сдвига G называют модуль упругости для деформации сдвига. Он равен отношению касательного напряжения τ к деформации сдвига (углу сдвига) γ:
G = τ/γ.
Модуль сдвига, модуль Юнга и коэффициент Пуассона связаны соотношением
G = (1 + μ)E/2. (7.31)
Отсюда следует, что модуль сдвига выражается в тех же единицах, что и модуль Юнга, т.е. в паскалях, и имеет размерность:
dim G = L-1MT-2.
Жесткость. Жесткость - величина, равная отношению упругой силы F, возникающей в теле при его растяжении, к абсолютной деформации Δl. Жесткость k является коэффициентом пропорциональности в законе Гука, записанном в виде
F = -kΔl.
Из этой формулы получим
|k| = F/Δl. (7.32)
Положив F = 1 H, Δl = 1 м, найдем единицу жесткости:
[k] = 1 Н/1 м = 1 H/м.
Ньютон на метр равен жесткости тела, в котором возникает упругая сила 1 Н при абсолютном удлинении этого тела на 1 м. Размерность жесткости:
dim k = MT-2.
Коэффициент трения скольжения. Коэффициент трения скольжения f есть коэффициент пропорциональности между силой F трения скольжения и силой Рn нормального давления. Из формулы силы трения
F = fPn
получим
f = F/Pn. (7.33)
Положив F = 1 Н, Рn = 1 H, найдем единицу трения скольжения:
[f] = 1 Н/1 Н = 1,
т.е. коэффициент трения - величина безразмерная и выражается в безразмерных единицах.
Безразмерным является также и истинный коэффициент трения скольжения μ, входящий в двучленный закон трения:
F = μ(Pn + Sp0),
где р0 - добавочное давление, вызванное силами молекулярного взаимодействия, S - площадь контакта между телами.
Коэффициент трения качения. Сила F трения качения определяется по закону Кулона
F = kPn/r,
где Рn - сила нормального давления, r - радиус катящегося тела (круглого цилиндра, шара), k - коэффициент трения качения. Отсюда
k = Fr/Pn. (7.34)
Положив здесь F = 1 Н, Рn = 1 Н, r = 1 м, получим единицу коэффициента трения качения:
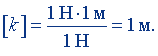
Следовательно, коэффициент трения качения выражается в метрах и имеет размерность:
dim k = L.
Напряженность гравитационного поля. Напряженностью G гравитационного поля называют физическую величину, равную отношению силы F, с которой поле действует на тело, помещенное в данную точку, к его массе m, т.е.
G = F/m. (7.35)
Положив F = 1 Н, m = 1 кг, получим единицу напряженности гравитационного поля:
[G] = 1 Н/1 кг = 1 Н/кг.
Ньютон на килограмм равен напряженности гравитационного поля, которое на материальную точку массой 1 кг действует с силой 1 Н. Размерность напряженности гравитационного поля:
dim G = LT-2.
Следовательно, напряженность гравитационного поля имеет размерность ускорения.
Потенциал гравитационного поля. Потенциалом φ гравитационного поля называют физическую величину, равную отношению потенциальной энергии П, которой обладает в гравитационном поле материальная точка, к массе m этой точки, т.е.
φ = П/m. (7.36)
Положив П = 1 Дж, m = 1 кг, получим единицу потенциала гравитационного поля:
[φ] = 1 Дж/1 кг = 1 Дж/кг.
Джоуль на килограмм равен потенциалу гравитационного ноля, в котором материальная точка массой 1 кг обладает потенциальной энергией 1 Дж. Размерность потенциала гравитационного поля:
dim φ = L2T-2.
Градиент потенциала гравитационного поля. Градиентом потенциала гравитационного поля называют векторную величину, направленную в сторону максимального возрастания потенциала вдоль нормали к поверхности равного потенциала и равную отношению разности потенциалов двух точек, лежащих на нормали, к расстоянию между ними. В общем случае градиент потенциала определяется по формуле
grad φ = -dφ/dr·i,
где i - единичный вектор нормали; dr - элемент нормали к эквипотенциальной поверхности. В случае однородного гравитационного поля
grad φ = (φ1 - φ2)/d·i, (7.37)
где φ1 и φ2 - потенциалы в двух точках поля, d - расстояние между поверхностями равного потенциала, проходящими через эти точки.
Положив в (7.37) φ1 - φ2 = 1 Дж/кг, d = 1 м, i = |i| = l, получим
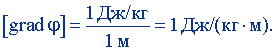
Эта единица называется джоуль на килограмм-метр. Размерность градиента потенциала:
dim grad φ = LT-2.
В теории поля доказывается, что градиент потенциала равен напряженности поля, взятой с обратным знаком, т.е.
G = -grad φ.
Отсюда следует, что напряженность поля может выражаться в тех же единицах, что и градиент потенциала, т.е. в джоулях на килограмм-метр.
Градиент скорости. Градиентом скорости называют векторную величину, определяемую соотношением
grad v = dv/dl·i, (7.38)
где dl - элемент нормали к поверхности слоя жидкости (газа); i - единичный вектор нормали. Градиент показывает быстроту изменения скорости при переходе от одного слоя жидкости (газа) к другому слою. Из формулы (7.38) следует
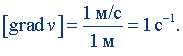
Эта единица называется секунда в минус первой степени. Размерность градиента скорости:
dim grad v = T-1.
Динамическая вязкость (коэффициент вязкости, коэффициент внутреннего трения). Динамическую вязкость η можно определить по формуле, выражающей силу внутреннего трения:
где dv/dl - градиент скорости, ΔS - площадь поверхности слоя, на которую рассчитывается сила внутреннего трения. Из этой формулы получим
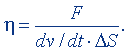(7.39)
Положив F = 1 Н, ΔS = 1 м2,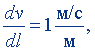 
найдем
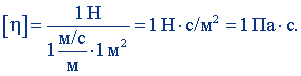
Паскаль-секунда равна динамической вязкости среды, касательное напряжение в которой при ламинарном течении и при разности скоростей слоев, находящихся на расстоянии 1 м по нормали к направлению скорости, равной 1 м/с, равно 1 Па. Размерность динамической вязкости:
dim η = L-1MT-1.
Кинематическая вязкость. Кинематической вязкостью называют величину, равную отношению динамической вязкости η жидкости (газа) к ее плотности ρ, т.е.
ν = η/ρ. (7.40)
Положив η = 1 Н·с/м2, ρ = 1 кг/м3, получим
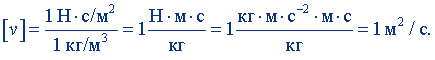
Квадратный метр на секунду равен кинематической вязкости, при которой динамическая вязкость среды плотностью 1 кг/м3, равна 1 Па·с. Размерность кинематической вязкости:
dim ν = L2T-1.
§ 8. ПРОИЗВОДНЫЕ ЕДИНИЦЫ ВЕЛИЧИН МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ
Единицы всех величин молекулярной физики и термодинамики могут быть выражены через пять основных единиц Международной системы - метр, килограмм, секунду, кельвин, моль.
Относительные атомная и молекулярная массы *. Относительная атомная масса Аr химического элемента есть отношение массы ma атома данного элемента к 1/12 массы атома изотопа углерода 12C, т.е.
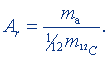(8.1)
Относительная молекулярная масса Мr вещества есть отношение массы mM молекулы данного вещества к 1/12 части массы атома изотопа углерода 12С, т.е.
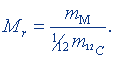(8.2)
Из формул (8.1) и (8.2) следует, что относительная атомная масса и относительная молекулярная масса - величины безразмерные и выражаются в безразмерных единицах.
* Ранее эти величины назывались соответственно атомным весом и молекулярным весом. Однако такие наименования неточно выражают смысл, который вкладывается в понятия "относительная молекулярная масса" и "относительная атомная масса". Происхождение терминов "молекулярный вес" и "атомный вес" исторически объясняется тем, что раньше "масса" и "вес" отождествлялись.
Постоянная Авогадро. Постоянная Авогадро NA есть величина, равная отношению числа N молекул, содержащихся в системе, к количеству вещества ν данной системы, т.е.
NA = N/ν. (8.3)
Из этой формулы получим единицу постоянной Авогадро:
[NA] = 1/1 моль = 1 моль-1.
Размерность постоянной Авогадро:
dim NA = N-1.
Концентрация молекул (объемное число молекул). Концентрацией n называют величину, равную отношению N молекул, содержащихся в системе, к ее объему V, т.е.
n = N/V. (8.4)
Положив N = 1, V = 1 м3, найдем единицу концентрации молекул:
[n] = 1/1 м3 = 1 м-3.
Размерность концентрации молекул:
dim n = L-3.
Молярная масса. Молярная масса М вещества есть величина, равная отношению массы m системы к количеству вещества ν этой системы, т.е.
М = m/ν. (8.5)
Положив в этой формуле m = 1 кг, ν = 1 моль, получим единицу молярной массы:
[М] = 1 кг/1 моль = 1 кг/моль.
Килограмм на моль равен молярной массе вещества, имеющего при количестве вещества 1 моль массу 1 кг. Размерность молярной массы:
dim M = MN-1.
В некоторых учебных пособиях по курсу общей физики молярная масса как особая величина не вводится, а отождествляется с относительной молекулярной массой. Но относительная молекулярная масса - величина безразмерная и выражается в безразмерных единицах, молярная же масса - величина размерная и выражается в килограммах на моль.
Молярная масса входит в уравнение Клапейрона-Менделеева
pV = m/M·RT,
где ν = m/M - количество вещества. Если здесь М считать, как это нередко делают, относительной молекулярной массой, то размерности левой и правой частей этого равенства будут разными. В самом деле, размерность левой части
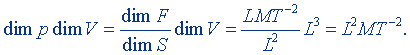
Если учесть, что
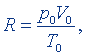
где p0 и Т0 - давление и температура при нормальных условиях, V0 - молярный объем, то размерность правой части
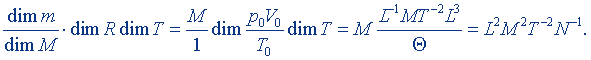
Ясно, что
L2MT-2 ≠ L2M2T-2N-1.
Если же в уравнении Клапейропа - Менделеева М считать молярной массой, правая часть этого уравнения имеет такую же размерность, что и левая, т.е. L2MT-2.
Молярная (универсальная) газовая постоянная. Молярной газовой постоянной R называют физическую величину, равную отношению работы А, совершаемой идеальным газом при изобарическом его нагревании, к интервалу ΔТ температур и количеству вещества ν нагреваемого газа, т.е.
R = A/(νΔT). (8.6)
Положив А = 1 Дж, ν = 1 моль, ΔT = 1 К, получим единицу молярной газовой постоянной:
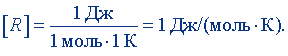
Подставив размерности величин, входящих в правую часть равенства (8.6), найдем размерность молярной газовой постоянной:
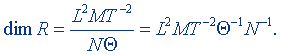
⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨
МЕНЮ САЙТА / СОДЕРЖАНИЕ