Ł Старые понятные учебники советских времен по физике, математике. Акупунктура, похудение

ЧЕРТОВ А.Г. "ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН", 1977

Относительная плотность. Относительной плотностью вещества называют величину, равную отношению его плотности к плотности некоторого вещества при определенных физических условиях. Таким стандартным веществом является вода при температуре 3,98°С и нормальном атмосферном давлении (101 325 Па) или сухой воздух при 20°С и нормальном атмосферном давлении.

Относительная плотность

d = ρ/ρ₀, (7.12)

где ρ - плотность данного вещества, ρ₀ - плотность стандартного вещества.

Положив в формуле (7.12) ρ = 1 кг/м³, ρ₀ = 1 кг/м³, получим единицу относительной плотности:

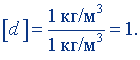
Следовательно, относительная плотность выражается в безразмерных единицах.

Удельный объем. Удельным объемом называют величину, равную отношению объема V тела к его массе m:

υ = V/m. (7.13)

Положив V = 1 м³, m = 1 кг, получим единицу удельного объема:

[υ] = 1 м³/1 кг = 1 м³/кг.

Кубический метр на килограмм равен удельному объему однородного вещества, объем которого при массе 1 кг ра

вен 1 м³. Размерность удельного объема:

dim υ = L³M^-1.

Из сравнения формул (7.11) и (7.13), а также размерностей удельного объема и плотности следует, что удельный объем есть величина, обратная плотности.

Удельный вес. Удельным весом тела называют физическую величину, определяемую соотношением

γ = dG/dV.

Для однородного тела

γ = G/V, (7.14)

где G - вес тела, V - его объем.

Положив в (7.14) G = 1 Н, V = 1 м³, получим единицу удельного веса

[γ] = 1 Н/1 м³ = 1 Н/м³.

Ньютон на кубический метр равен удельному весу однородного вещества, вес которого при объеме 1 м³ равен 1 Н. Размерность удельного веса:

dim γ = L^-2MT^-2.

Давление. Давлением р называют физическую величину, равную отношению силы dF, действующей на элемент поверхности нормально к ней, к площади dS этого элемента, т.е.

p = dF/dS.

При равномерном распределении силы F по поверхности площадью S давление выражается формулой

p = F/S. (7.15)

Положив F = 1 H, S = 1 мг, получим единицу давления:

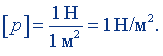
Эта единица называется паскаль * (Па). Паскаль равен давлению, вызываемому силой 1 Н, равномерно распределенной по нормальной к ней поверхности площадью 1 м². Размерность давления:

dim p = L^-1MT^-2.

* Наименование единицы давления и механического напряжения - паскаль (Па) было принято на XIV Генеральной конференции по мерам и весам (1971 г.).

Импульс (количество движения). Импульсом р тела называют величину, равную произведению массы тела на его скорость, т.е.

p = mv. (7.16)

Положив m = 1 кг, м/с, получим единицу импульса:

[р] = 1 кг · 1 м/с = 1 кг·м/с.

Килограмм-метр в секунду равен импульсу (количеству движения) тела массой 1 кг, движущегося поступательно со скоростью 1 м/с. Размерность импульса:

dim p = LMT^-1.

Импульс силы. Импульсом силы I называют физическую величину, равную произведению силы на время ее действия, т.е.

I = Ft. (7.17)

Положив F = 1 Н, t = 1 с, получим единицу импульса силы:

[I] = 1 Н · 1 с = 1 Н·с.

Ньютон-секунда равен импульсу силы, создаваемому силой 1 Н, действующей в течение времени 1 с. Размерность импульса силы:

dim I = LMT^-1.

Сравнив размерности импульса силы и импульса, видим, что они одинаковы. Это следует и из второго закона Ньютона:

FΔt = mΔv.

Работа, механическая энергия. Работой dA называют величину, равную скалярному произведению силы F на бесконечно малое перемещение dr тела под действием этой силы:

dA = F·dr = F cos α dr.

При прямолинейном движении тела на пути s под действием постоянной силы F работа определяется по формуле

A = F s cos α, (7.18)

где α - угол между направлениями действия силы и движения тела.

Положив в (7.18) F = 1 Н, s = 1 м, α = 0, получим

[А] = 1 Н · 1 м = 1 Н·м.

Эта единица называется джоуль (Дж). Джоуль равен работе, совершаемой при перемещении точки приложения силы 1 Н на расстояние 1 м в направлении действия силы. Размерность работы:

dim A = L²MT^-2.

Кинетическая энергия. Кинетической энергией Т называют энергию движущегося тела и определяют по формуле

T = mv²/2, (7.19)

где m - масса тела, v - его скорость.

Положив в (7.19) m = 2 кг, v = 1 м/с², найдем единицу кинетической энергии:

[Т] = 1/2 · 2 кг · 1 м/с² = 1 кг·м·с^-2 = 1 Дж.

Следовательно, кинетическая энергия выражается в тех же единицах, что и работа, т.е. в джоулях. Размерность кинетической энергии:

dim T = L²MT^-2.

Потенциальная энергия. Потенциальной энергией Π называют энергию взаимодействия тел. Единицу этой энергии определим по формуле потенциальной энергии тела массой m, поднятого над Землей на высоту h над ее поверхностью:

Π = mgh. (7.20)

Положив m = 1 кг, g = 9,81 м/с², h = 1/9,81 м, найдем [П] = 1 кг · 9,81 м/с² · 1/9,81 м = 1 кг·м·с^-2 = 1 Дж.

Следовательно, потенциальная энергия выражается в джоулях. Размерность потенциальной энергии:

dim Π = L²MT^-2.

Коэффициент полезного действия. Коэффициент полезного действия η - относительная величина, равная отношению полезно использованной энергии Е_пол к суммарной энергии Е_сум, полученной системой, т.е.

η = Е_пол/Е_сум.

Положив Е_пол = 1 Дж, Е_сум = 1 Дж, получим единицу коэффициента полезного действия:

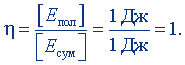
Следовательно, коэффициент полезного действия, как и любая относительная величина, выражается в безразмерных единицах.

Мощность. Мощность есть физическая величина, равная отношению работы dA к бесконечно малому промежутку времени dt, в течение которого эта работа совершается:

N = dA/dt.

В случае постоянной мощности формула принимает вид

N = A/t. (7.21)

Положив А = 1 Дж, t = 1 с, получим единицу мощности:

[N] = 1 Дж/1 с = 1 Дж/с.

Эта единица носит название ватт (Вт). Ватт равен мощности, при которой за время 1 с совершается работа в 1 Дж. Размерность мощности:

dim N = L²MT^-3.

Момент силы. Моментом силы М относительно некоторой точки называют величину, равную произведению силы F на расстояние r от этой точки до линии, вдоль которой действует сила:

M = Fr. (7.22)

Подставив F = 1 Н, r = 1 м, получим единицу момента силы:

[M] = 1 Н · 1 м = 1 Н·м.

Ньютон-метр равен моменту силы, создаваемому силой 1 Н относительно точки, расположенной на расстоянии 1 м от линии действия силы. Размерность момента силы:

dim M = L²MT^-2.

Момент инерции (динамический момент инерции). Моментом инерции J тела относительно некоторой оси инерции называют величину, равную сумме произведений масс всех частиц тела на квадраты их расстояний от этой оси. Единицу момента инерции удобно определить по формуле момента инерции материальной точки относительно некоторой оси инерции:

J = mr², (7.23)

где m - масса материальной точки, r - расстояние ее до оси инерции.

Положив в (7.23) m = 1 кг, r = 1 м, получим единицу момента инерции:

[J] = 1 кг · 1 м² = 1 кг·м².

Килограмм-метр в квадрате равен моменту инерции материальной точки массой 1 кг, находящейся на расстоянии 1 м от оси инерции. Размерность момента инерции:

dim J = L²M.

Момент импульса (момент количества движения). Моментом импульса L тела называют величину, равную произведению момента инерции J тела на его угловую скорость ω:

L = Jω. (7.24)

Момент импульса тела равен сумме моментов импульса всех его частиц (материальных точек).

Момент импульса материальной точки относительно некоторой точки (полюса) есть произведение длины радиуса-вектора r материальной точки, проведенного из полюса, на ее импульс, т.е.

L = rp = mvr, (7.25)

где р - импульс материальной точки, m и v - ее масса и скорость.

Подставив в (7.25) m = 1 кг, v = 1 м/с, r = 1 м, получим единицу момента импульса:

[L] = 1 кг · 1 м/с · 1 м = 1 кг · м²/с.

Килограмм-метр в квадрате в секунду равен моменту импульса (моменту количества движения) тела с моментом инерции 1 кг·м², вращающегося с угловой скоростью 1 рад/с. Единица момента импульса получена по формуле (7.25), а определение единицы дано на основе формулы (7.24). Обе указанные формулы дают одинаковую размерность момента импульса:

dim L = L²MT^-1.

Относительное удлинение. Относительным удлинением ε называют величину, равную отношению абсолютного удлинения Δl тела к первоначальной его длине l₀:

ε = Δl/l₀. (7.26)

Подставив Δl = 1 м, l₀ = 1 м, найдем единицу относительного удлинения:

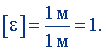
Относительное удлинение выражается в безразмерных единицах. В безразмерных единицах выражаются также другие виды относительной деформации: относительное поперечное сжатие, относительный сдвиг и т.д.

Нормальное механическое напряжение (нормальное напряжение). Нормальным напряжением σ называют физическую величину, равную отношению упругой силы к площади перпендикулярного силе сечения тела, т.е.

σ = dF/dS.

При равномерном распределении напряжения оно может быть выражено формулой

σ = F/S. (7.27)

Подставив F = 1 Н, S = 1 м², получим единицу нормального напряжения:

[σ] = 1 Н/1 м² = 1 Н/м².

Напряжение выражается в тех же единицах, что и давление, т.е. в паскалях.

В паскалях выражаются касательное напряжение и все критические значения напряжений: предел пропорциональности σ_п, предел текучести σ_т, предел прочности σ_пр и др. Размерность напряжения:

dim σ = L^-1MT^-2.

Модуль упругости. Модуль упругости - величина, равная отношению напряжения к относительному удлинению. Единицу модуля упругости К найдем по закону Гука:

σ = Кε. (7.28)

Так как ε - безразмерная величина, то модуль упругости, как это следует из формулы (7.28), выражается в тех же единицах, что и напряжение, т.е. в паскалях, и имеет ту же размерность:

dim K = L^-1MT^-2.

Модуль Юнга (модуль продольной упругости). Для случая продольной деформации (линейного растяжения или

сжатия) закон Гука имеет вид

σ = Еε, (7.29)

где E - модуль Юнга. Он равен тому напряжению, при котором относительное удлинение равно единице, а абсолютное удлинение - первоначальной длине. Из этого определения, а также из формулы (7.29) следует, что единицей модуля Юнга является паскаль, а его размерность:

dim E = L^-1MT^-2.

⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨

МЕНЮ САЙТА / СОДЕРЖАНИЕ