
Я создала и активно наполняю телеграм-канал "Перець". Здесь лучшие карикатуры из журнала, начиная с 1922 года.
Заходите, подписывайтесь: https://t.me/cartalana

ЧЕРТОВ А.Г. "ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН", 1977
Глава II. МЕЖДУНАРОДНАЯ СИСТЕМА ЕДИНИЦ (СИ)
§ 6. ОСНОВНЫЕ, ДОПОЛНИТЕЛЬНЫЕ И ПРОИЗВОДНЫЕ ЕДИНИЦЫ СИСТЕМЫ
1. Метр (м) - единица длины. Метр равен длине 1 650 763,73 волн в вакууме излучения, соответствующего переходу между уровнями 2р10 и 5d5 атома криптона-86.
2. Килограмм (кг) - единица массы. Килограмм равен массе международного прототипа килограмма.
3. Секунда (с) - единица времени. Секунда равна 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133.
4. Ампер (А) - единица силы тока. Ампер равен силе неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади сечения, расположенным в вакууме на расстоянии 1 м один от другого, вызвал бы на участке проводника длиной 1 м силу взаимодействия, равную 2· 10-7 Н.
5. Кельвин (К) - единица термодинамической температуры. Кельвин равен 1/273,16 части термодинамической температуры тройной точки воды.
В Кельвинах выражается также интервал или разность температур.
6. Моль (моль) - единица количества вещества. Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде-12 массой 0,012 кг.
При применении моля структурные элементы должны быть специфицированы и могут быть атомами, молекулами, ионами, электронами и другими частицами или специфицированными группами частиц.
7. Кандела (кд) - единица силы света. Кандела равна силе света, испускаемого с поверхности площадью 1/600 000 м2 полного излучателя в перпендикулярном направлении при температуре излучателя, равной температуре затвердевания платины при давлении 101 325 Па.
Радиан (рад) - единица плоского угла. Радиан равен углу между двумя радиусами окружности, длина дуги между которыми равна радиусу.
Стерадиан (ср) - единица телесного угла. Стерадиан равен телесному углу с вершиной в центре сферы, вырезающему на поверхности сферы площадь, равную площади квадрата со стороной, равной радиусу сферы.
Производные единицы Международной системы образуются из основных и дополнительных единиц при помощи определяющих уравнений в соответствии с принципами построения систем единиц, изложенными в § 1, 2, 4.
Для получения производных единиц в каждом разделе курса физики необходимо определяющие уравнения расположить в последовательности, удовлетворяющей условиям, указанным в таблице (последовательность величин).
В § 7-13 получены производные единицы и размерности производных величин всех разделов курса общей физики.
В когерентную систему единиц может входить только по одной единице для каждой физической величины. Поэтому в данной главе, где дано построение Международной системы единиц, для каждой физической величины указывается только одна единица. Единицы величин в других системах и внесистемные (в том числе кратные и дольные) единицы приводятся в гл. III и IV, а также в справочных таблицах.
§ 7. ПРОИЗВОДНЫЕ ЕДИНИЦЫ МЕХАНИЧЕСКИХ ВЕЛИЧИН
Все производные единицы механических величин могут быть выражены через три основные единицы Международной системы - метр, килограмм, секунду и дополнительную единицу - радиан.
При построении системы единиц механических величин коэффициент пропорциональности во всех формулах принимается равным безразмерной единице.
Единицы пространства. Единицы величин кинематики
Площадь. Единицу площади S найдем по формуле площади квадрата:
S = a2, (7.1)
где а - длина его стороны. Положив а = 1 м, получим
[S] = 1 м2.
Квадратный метр равен площади квадрата со сторонами, длины которых равны 1 м. Размерность площади
dim S = L2.
Объем. Вместимость. Единицу объема V получим по формуле объема куба:
V = а3, (7.2)
где а - длина его ребра.
Положив в формуле (7.2) а = 1 м, получим
[V] = 1 м3.
Кубический метр равен объему куба с ребрами, длины которых равны 1 м. Размерность объема:
dim V = L3.
Скорость. Скорость - физическая величина, равная первой производной от перемещения по времени, т.е.
v = dr/dt.
Для равномерного движения значение скорости может быть определено как отношение пути Δs ко времени Δt, за которое этот путь пройден:
v = Δs/Δt. (7.3)
Положив в (7.3) Δs = 1 м, Δt = 1 с, получим единицу скорости
[v] = 1 м/1 с = 1 м/с.
Эта единица носит название метр в секунду. Метр в секунду равен скорости прямолинейно и равномерно движущейся точки, при которой эта точка за время 1 с перемещается на расстояние 1 м. Размерность скорости:
dim v = LT-1.
Ускорение. Ускорением называют физическую величину, равную первой производной от скорости по времени, т.е.
a = dv/dt.
В случае равнопеременного движения, для которого ускорение есть величина постоянная, оно может быть определено по формуле
a = Δv/Δt, (7.4)
где Δv - изменение скорости равнопеременного движения за время Δt.
Положив в (7.4) Δv = 1 м/с, Δt = 1 с, получим
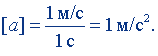
Эта единица называется метр на секунду в квадрате. Метр на секунду в квадрате равен ускорению прямолинейно и равноускоренно движущейся точки, при котором за время 1 с скорость точки возрастает на 1 м/с. Размерность ускорения:
dim a = LT-2.
Период. Период - это время, в течение которого совершается один цикл периодического процесса (колебаний, излучений и т.п.) или одно дискретное событие (импульс, удар и т.п.).
Период Т выражается в единицах времени (в СИ - в секундах).
Частота. Следует различать частоту периодического процесса (колебаний, излучений и т.п.), частоту дискретных событий (импульсов и т.п.) и частоту вращения.
Частотой ν, f периодического процесса называют физическую величину, равную числу циклов, происходящих за единицу времени. Из этого определения следует, что частота есть величина, обратная периоду, т.е.
ν = 1/T. (7.5)
Положив в (7.5) Т = 1 с, найдем
[ν] = 1/1 c = 1 с-1.
Эта единица называется герцем (Гц). Герц равен частоте периодического процесса, при которой за время 1 с происходит один цикл периодического процесса.
Частотой n дискретных событий называют физическую величину, равную числу событий, происходящих в единицу времени. Частота дискретных событий и время τ, затрачиваемое на одно событие, связаны
формулой
n = 1/τ. (7.6)
Отсюда единица частоты дискретных событий:
[n] = 1/1 с = 1 с-1.
Эта единица называется секунда в минус первой степени. Секунда в минус первой степени равна частоте дискретных событий, при которой за время 1 с совершается одно событие.
Частотой n вращения называют величину, равную числу полных оборотов за единицу времени. Частота n вращения определяется по формуле
n = 1/τ,
где τ - время, в течение которого совершается один полный оборот.
Положив в этой формуле τ = 1 с, найдем
[n] = 1/1 с = 1 с-1.
Секунда в минус первой степени равна частоте вращения, при которой за 1 с происходит один цикл вращения (один оборот). Размерность частоты:
dim ν = dim n = T-1.
Кривизна. Кривизна кривой характеризует степень отличия ее от прямой. В общем случае кривизна кривой в разных ее точках различна, и только кривизна окружности во всех ее точках одна и та же.
Кривизна К кривой в некоторой ее точке есть величина, обратная радиусу R кривизны, т.е.
K = 1/R. (7.7)
Радиус кривизны - это радиус соприкасающейся окружности.
Для получения единицы кривизны положим в (7.7) R = 1 м. Тогда
[K] = 1/1 м = 1 м-1.
Эта единица называется метр в минус первой степени. Размерность кривизны:
dim K = L-1.
Угловая скорость. Угловой скоростью со называют физическую величину, равную первой производной от угла поворота тела по времени, т.е.
ω = dφ/dt.
При равномерном вращательном движении тела угловая скорость - это величина, равная отношению угла поворота Δφ к интервалу времени Δt, за которое произошел этот поворот:
ω = Δφ/Δt. (7.8)
Положив Δφ = 1 рад, Δt = 1 с, получим
[ω] = 1 рад/1 с = 1 рад/с.
Радиан в секунду равен угловой скорости равномерно вращающегося тела, при которой за время 1 с совершается поворот тела относительно оси вращения на угол 1 рад.
Так как плоский угол является не основной, а дополнительной величиной Международной системы, то в размерность производных величин он не входит. Учитывая это, из формулы (7.8) найдем размерность угловой скорости:
dim ω = Т-1.
Угловое ускорение. Угловым ускорением называют физическую величину, определяемую первой производной от угловой скорости по времени:
ε = dω/dt.
При равноускоренном вращении тела угловое ускорение есть величина, равная отношению изменения Δω угловой скорости ко времени Δt, в течение которого произошло это изменение:
ε = Δω/Δt. (7.9)
Положив в (7.9) Δω = 1 рад/с, Δt = 1 с, получим
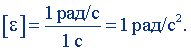
Радиан на секунду в квадрате равен угловому ускорению равноускоренно вращающегося тела, при котором за время 1 с угловая скорость тела возрастает на 1 рад/с. Размерность углового ускорения:
dim ε = T-2.
Сила. Сила - это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей. Единицу силы F найдем по формуле, выражающей второй закон Ньютона:
F = ma, (7.10)
где m - масса тела, a - ускорение, сообщаемое этому телу силой F.
Положив в (7.10) m = 1 кг, а = 1 м/с2, получим
[F] = 1 кг · 1 м/с2 = 1 кг · м/с2.
Эта единица носит название ньютон (Н). Ньютон равен силе, сообщающей телу массой 1 кг ускорение 1 м/с2 в направлении действия силы.
В ньютонах выражается также вес тела G. Вес тела - это сила, с которой тело действует на подвес или подставку, поддерживающую это тело. В случае, если подставка или подвес не имеют ускорения в вертикальном направлении, вес тела связан с его массой соотношением:
G = mg,
где g - ускорение свободного падения.
Размерность силы, а следовательно, и веса:
dim F = LMT-2.
Плотность. Плотностью ρ вещества называют физическую величину, определяемую отношением
ρ = dm/dV.
В случае однородного тела плотность
ρ = m/V, (7.11)
где m - масса тела, V - его объем.
Положив в (7.11) m = 1 кг, V = 1 м3, получим единицу плотности
[ρ] = 1 кг/1 м3 = 1 кг/м3.
Килограмм на кубический метр равен плотности однородного вещества, масса которого при объеме 1 м3 равна 1 кг. Размерность плотности:
dim ρ = L-3M.
Относительная величина. Относительной величиной называют величину, равную безразмерному отношению физической величины к одноименной величине, принимаемой за исходную.
Если некоторая величина X имеет размерность LpMqTr, то и однородная (одноименная) ей величина Х0 имеет такую же размерность. Следовательно, относительная величина
ε = Х/Х0
имеет размерность
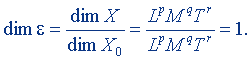
Все относительные величины выражаются в безразмерных единицах. Безразмерная единица равна относительной величине, равной 1.
⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨
МЕНЮ САЙТА / СОДЕРЖАНИЕ