Ł Старые понятные учебники советских времен по физике, математике. Акупунктура, похудение

ШВЕЦОВ К.И., БЕВЗ Г.П."СПРАВОЧНИК ПО ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ. АРИФМЕТИКА, АЛГЕБРА", 1965

2. Логарифмическая функция. Функция, которую можно выразить формулой 𝑦 = log_𝑎𝑥, где 𝑥 - аргумент, а 𝑎 ≠ 1 положительное число, называется логарифмической функцией.

Примеры логарифмических функций:

𝑦 = log₂𝑥, 𝑦 = log_π𝑥, 𝑦 = log₁₀𝑥.

Логарифмическая функция 𝑦 = log₂𝑥 обратная показательной функции 𝑦 = 𝑎^𝑥. Поэтому их графики симметричны относительно биссектрисы первого и третьего координатных углов (рис. 61).

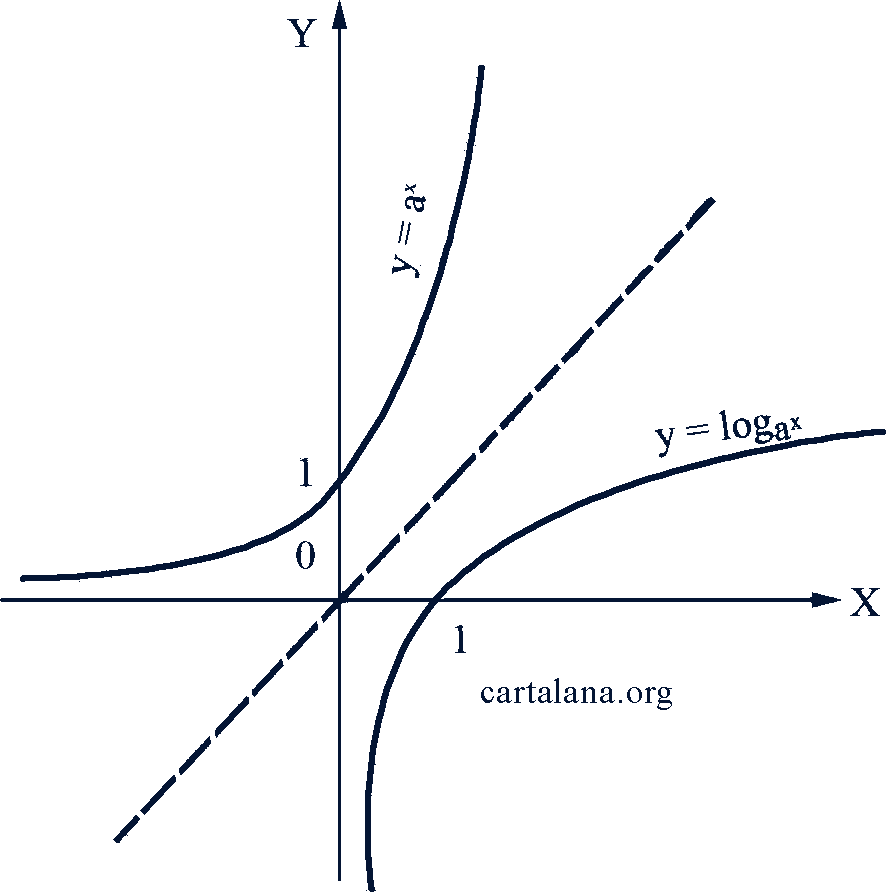
Рис. 61

На рис. 62 даны графики следующих логарифмических функций:

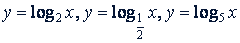
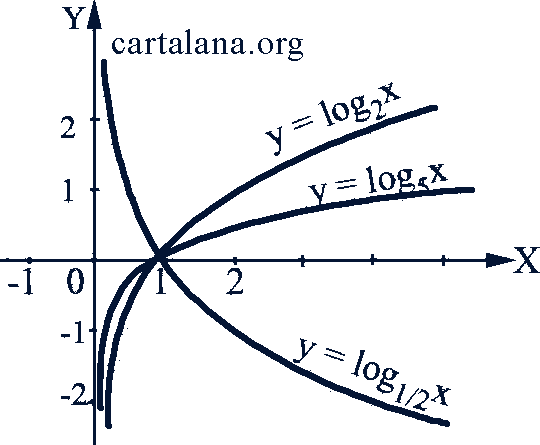
Рис. 62

3. Свойства логарифмов

а) Всякое положительное число по любому (Здесь и дальше мы имеем в виду любое положительное, не равное единице, основание логарифмов. Логарифмы рассматриваем только действительные) основанию имеет единственный логарифм.

б) При любом основании отрицательные числа не имеют логарифмов.

в) При любом основании логарифм единицы равен нулю.

г) Логарифм самого основания ранен единице.

д) При основании, большем единицы, большему числу соответствует и больший логарифм, при этом логарифмы чисел, больших единицы, положительны, а логарифмы чисел, меньших единицы, отрицательны.

При основании, меньшем единицы, большему числу соответствует меньший логарифм, при этом логарифмы чисел, меньших единицы, положительны, а логарифмы чисел, больших единицы, отрицательны.

е) Если основание логарифмов больше единицы, то при неограниченном возрастании числа неограниченно возрастает и его логарифм, а при стремлении числа (положительного) к нулю его логарифм, оставаясь отрицательным, неограниченно возрастает по абсолютной величине.

ж) Если основание логарифмов меньше единицы, то при неограниченном возрастании числа его логарифм, оставаясь отрицательным, неограниченно убывает, а при стремлении положительного числа к нулю, его логарифм неограниченно возрастает.

Все эти свойства нетрудно "увидеть", рассматривая графики логарифмических функций при разных основаниях. Однако их можно доказать и аналитически, не обращаясь к графикам.

4. Решение примеров с использованием свойств логарифмов.

Пример 1. Исходя из определения логарифма, найти:

а) Какое число имеет логарифм 2 при основании 7?

б) Найти логарифм 125 по основанию 5.

а) При каком основании логарифм числа 16 равен 4?

Решение.

а) 2 = log₇ 𝑥, 𝑥 = 7² = 49;

б) 𝑥 = log₅ 125, 5^𝑥 = 125, 𝑥 = 3;

в) 4 = log_𝑖16, 𝑥⁴ = 16, 𝑥 = 2.

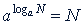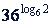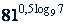Пример 2. На основании тождества найти: a) ; б) ; в) .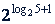

Решение.

а)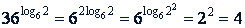

б)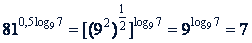

в)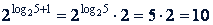

Пример 3. Что больше: log_𝑎 2 или log_𝑎 3?

Решение. Если 𝑎 > 1, то большему числу соответствует и больший логарифм, т.е. log_𝑎 2 < log_𝑎 3. Если 𝑎 < 1, то большему числу соответствует меньший логарифм, т.е. log_𝑎 2 > log_𝑎 3. Здесь предполагается, что

𝑎 > 0, 𝑎 ≠ 1.

Пример 4. Определить 𝑥, если:

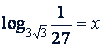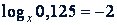а) ; б) ; в)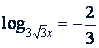

Решение.

а)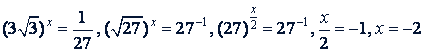

б)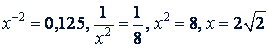

в)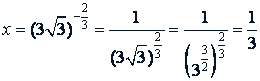

Пример 5. Определить 𝑥 из уравнений:

а) 5log₂ 𝑥 - 6 = 2log₂ 𝑥; б) (log₃ 𝑥)² - 3log₃ 𝑖 + 2 = 0.

Решение.

а) 5log₂ 𝑥 - 6 = 2log₂ 𝑥, 3log₂ 𝑖 = 6, log₂ 𝑖 = 2, 𝑖 - 2² = 4;

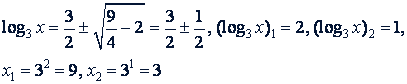
5. Переход от одного основания логарифмов к другому. Если надо перейти от логарифмов с основанием а к логарифмам с основанием b, пользуются следующим тождеством:

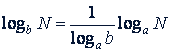
Множитель 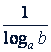называют модулем перехода.

Рассмотрим более подробно, как переходить от десятичных логарифмов к натуральным и наоборот.

Чтобы по известному десятичному логарифму числа 𝑛 найти его натуральный логарифм, нужно разделить десятичный логарифм числа 𝑛 на десятичный логарифм числа 𝑒 (последний равен 0,4343...).

Величина lg_𝑒 = 0,4343... называется модулем десятичных логарифмов и обозначается буквой 𝑀, так что

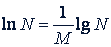
Например, из таблиц десятичных логарифмов имеем:

lg 2 = 0,3010. Отсюда .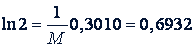

Чтобы по известному натуральному логарифму числа 𝑛 найти его десятичный логарифм, нужно умножить натуральный логарифм на модуль десятичных логарифмов 𝑀 = lg 𝑒 :

lg 𝑛 = lg 𝑒 · ln 𝑛 = 𝑀 · In 𝑛 = 0,4343𝑛.

Например, ln 3 = 1,0986, а отсюда lg 3 = 𝑚 · 1,0986 = 0,4771.

Очень часто в логарифмических преобразованиях пользуются также следующими формулами:

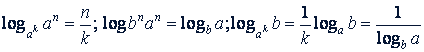
Пример 1. Что больше, log₄ 3 или log₁₆ 9?

Решение. Используя формулу 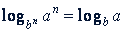, получаем

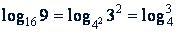
Пример 2. Вычислить 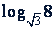, зная, что log₂ 3 = 𝑎.

Решение.

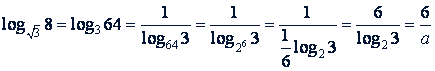
35. Логарифмирование и потенцирование

1. Логарифмирование. Логарифмировать алгебраическое выражение - значит выразить логарифм его через логарифмы отдельных чисел, входящих в это выражение. Это можно сделать, используя теоремы о логарифме произведения, частного, степени и корня.

Логарифм произведения равен сумме логарифмов сомножителей:

log (𝑎𝑏) = log 𝑎 + log 𝑏.

Логарифм частного (дроби) равен разности логарифмов делимого и делителя:

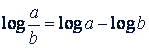
Логарифм степени равен произведению показателя степени на логарифм ее основания:

log 𝑎^𝑚 = 𝑚log 𝑎.

Логарифм корня равен частному от деления логарифма подкоренного числа на показатель корня:

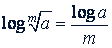
Примечание. При логарифмировании алгебраических выражений надо иметь в виду, что логарифм суммы не равен сумме логарифмов, т.е. нельзя вместо log(𝑎 + 𝑏) писать log 𝑎 + log 𝑏. Нельзя также вместо log (𝑎 - 𝑏) писать log 𝑎 - log 𝑏.

Логарифмирование алгебраических выражений проиллюстрируем на примерах.

Примеры. Прологарифмировать следующие выражения:

а) 𝑥 = 3𝑏𝑐; log 𝑥 = log 3 + log 𝑏 + log 𝑐.

б)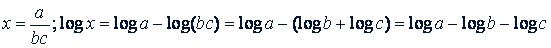

в)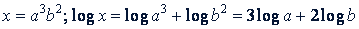

г)

д)

е)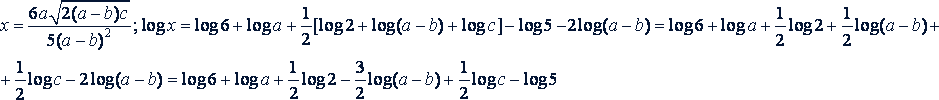

ж)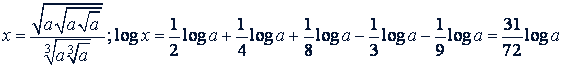

2. Потенцирование. Если по данному результату логарифмирования находят выражение, от которого получен этот результат, то такую операцию называют потенцированием.

Примеры. Пропотенцировать следующие выражения:

а)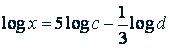

б)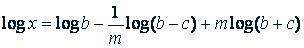

в)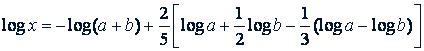

Решения.

а)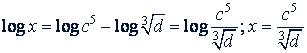

б)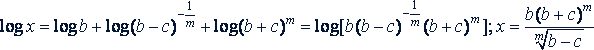

в)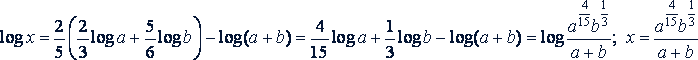

36. Десятичные логарифмы

1. Свойства десятичных логарифмов

а) Логарифм целого числа, изображенного единицей с последующими нулями, есть целое положительное число, содержащее столько единиц, сколько нулей в данном числе.

Примеры, lg 100 = 2; lg 10000 = 4.

б) Логарифм десятичной дроби, изображаемой единицей с предшествующими нулями, есть целое отрицательное число, содержащее столько отрицательных единиц, сколько нулей в изображении дроби, считая и 0 целых.

Примеры. lg 0,00001 = -5; lg 0,001 = -3.

в) Логарифм рационального числа, которое не является степенью 10 с целым показателем (положительным, отрицательным или нулевым), есть иррациональное число.

Логарифм иррационального числа может быть как рациональным, так и иррациональным числом. Например, 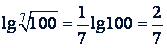(рациональное число), 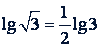(иррациональное число).

Целая часть логарифма называется его характеристикой, а дробная - мантиссой.

г) Характеристика логарифма числа, большего единицы, на единицу меньше числа цифр его целой части.

Примеры. lg 3,15 = 0, ...; lg 375 = 2, ...; lg 2000 = 3, ...

д) Характеристика логарифма числа, меньшего единицы, содержит столько отрицательных единиц, сколько нулей в этом числе предшествует первой значащей цифре, считая и нуль целых. При этом мантисса логарифма положительна.

Примеры.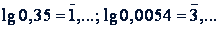

е) От умножения числа на 10, 100, 1000, ..., вообще на единицу с последующими нулями, мантисса логарифма не меняется, а характеристика увеличивается на столько единиц, сколько нулей в множителе.

От деления числа на единицу с нулями мантисса логарифма не изменяется, а характеристика уменьшается на столько единиц, сколько нулей в делителе.

Поэтому перенесение запятой в десятичной дроби на несколько знаков вправо или влево не изменяет мантиссы логарифма этой дроби, а только характеристику.

Таким образом, логарифмы чисел 0,00423; 0,0423; 4,23; 423 отличаются только характеристиками, но не мантиссами (при условии, что все мантиссы положительны). Мантиссы логарифмов чисел, имеющих одну и ту же значащую часть, одинаковы.

2. Преобразование отрицательного логарифма. Известно, что десятичные логарифмы чисел, меньших 1, отрицательны. Такие логарифмы всегда можно преобразовать так, что мантисса у них будет положительная, а характеристика - отрицательной. Это выполняется по следующему правилу.

Чтобы преобразовать логарифм с отрицательной мантиссой в логарифм с положительной мантиссой, надо к характеристике прибавить минус единицу, а к мантиссе прибавить плюс единицу.

Так, например, если мы имеем логарифм -2,3781, то можно его преобразовать так:

-2,3781 = -2 - 0,3781 = (-2 - 1) + (1 - 0,3781) = -3 + 0,6219 = .

Кратко эти действия записывают так:

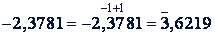
Примеры.

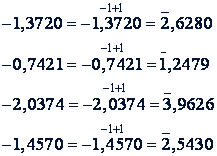
⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨

МЕНЮ САЙТА / СОДЕРЖАНИЕ