Ł Старые понятные учебники советских времен по физике, математике. Акупунктура, похудение

ШВЕЦОВ К.И., БЕВЗ Г.П."СПРАВОЧНИК ПО ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ. АРИФМЕТИКА, АЛГЕБРА", 1965

3. Обратно пропорциональная зависимость. Зависимость между величинами 𝑥 и 𝑦, которую можно выразить формулой

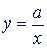где 𝑎 - некоторое заданное число, называют обратно пропорциональной зависимостью. Здесь 𝑎, 𝑥, 𝑦 могут быть не только положительными числами (как в арифметике), но и отрицательными. Поэтому приведенное здесь определение более общее, чем давалось в арифметике.

Графиком обратно пропорциональной зависимости есть кривая линия, состоящая из двух отдельных веток, расположенных в первом и третьем координатных углах при 𝑎 > 0 (рис. 39), или во втором и четвертом - при 𝑎 < 0 (рис. 40). Эта линия называется равносторонней гиперболой. Она симметрична относительно начала координат, так как функция 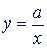нечетная. Эта функция неограниченна.

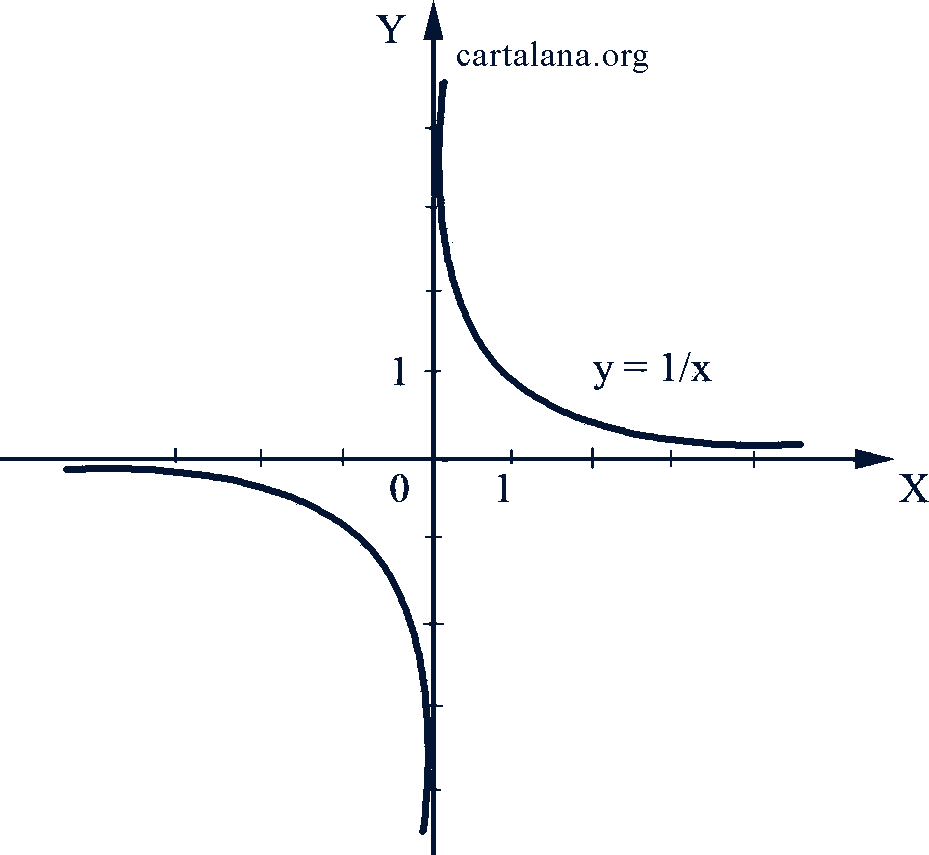
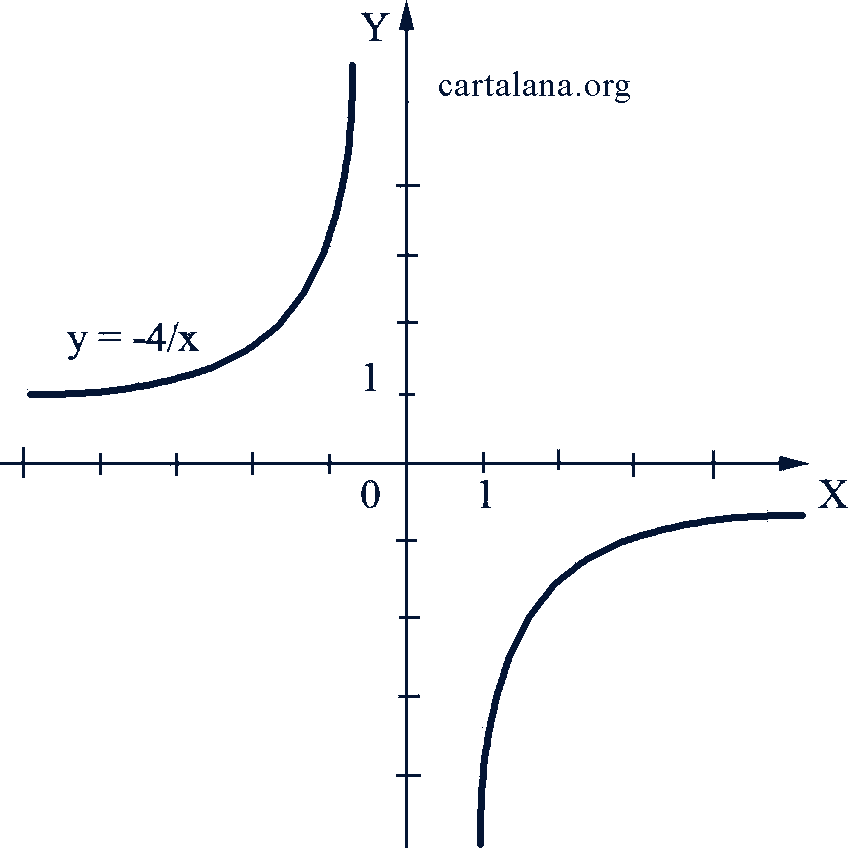
Рис. 39-40

При 𝑥 > 0 и 𝑥 < 0 эта функция убывающая, если 𝑎 > 0, и возрастающая, если 𝑎 < 0; при 𝑥 = 0 функция эта не определена, так как 𝑥 = 0 не принадлежит области допустимых значений аргумента.

4. Квадратичная функция. Квадратичной (или квадратной) называют функцию, которую можно выразить формулой

𝑦 = 𝑎𝑥² + 𝑏𝑥 + 𝑐,

где 𝑥 - аргумент; 𝑎 ≠ 0, 𝑏, 𝑐 - постоянные величины.

Простейшей квадратичной функцией есть функция вида 𝑦 = 𝑥². Это - неограниченная четная функция, определенная для всех действительных значений аргумента 𝑥. При 𝑥 > 0 она возрастающая, а при 𝑥 < 0 - убывающая. Ее график (рис. 41) есть кривая линия, называемая параболой. Она проходит через начало координат, симметрична оси ординат, ее ветки направлены вверх.

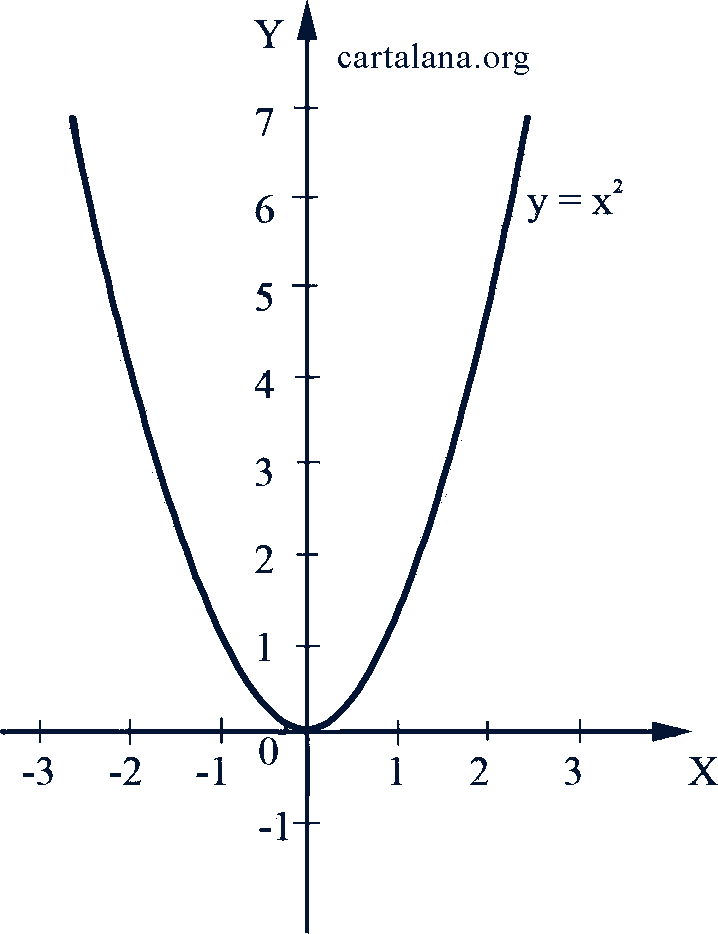
Рис. 41

Квадратичная функция вида 𝑦 = 𝑎𝑥² также четная, неограниченная, определенная для всех действительных 𝑥. Ее график также парабола, проходящая через начало координат и симметрична оси ординат. Но при положительных а ветки ее направлены вверх, а при 𝑎 < 0 - вниз. Чем меньше абсолютная величина 𝑎, тем дальше отходят ветки параболы от оси ординат, тем "шире" она (рис. 42).

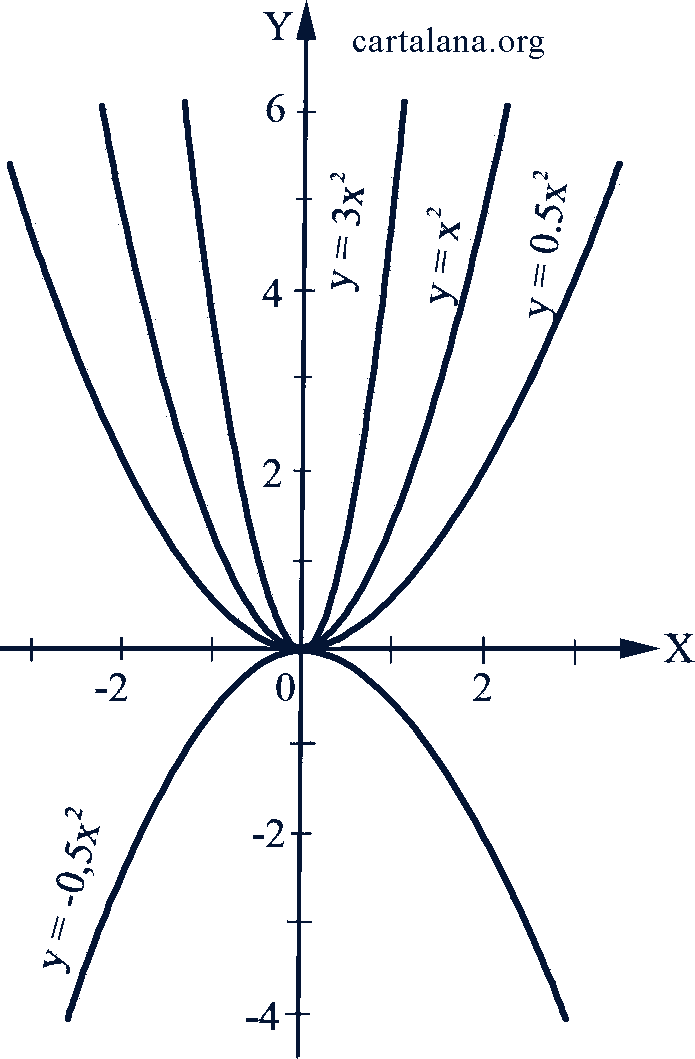
Рис. 42

График квадратной функции 𝑦 = 𝑎𝑥² + 𝑏𝑥 + 𝑐 - такая же пара бола, как и график функции 𝑦 = 𝑎𝑥², ее ветки также направлены вверх при 𝑎 > 0 или вниз при 𝑎 < 0, ее ось симметрии параллельна оси ординат. Только вершина этой параболы (рис. 43) находится не в начале координат, а в точке

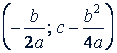
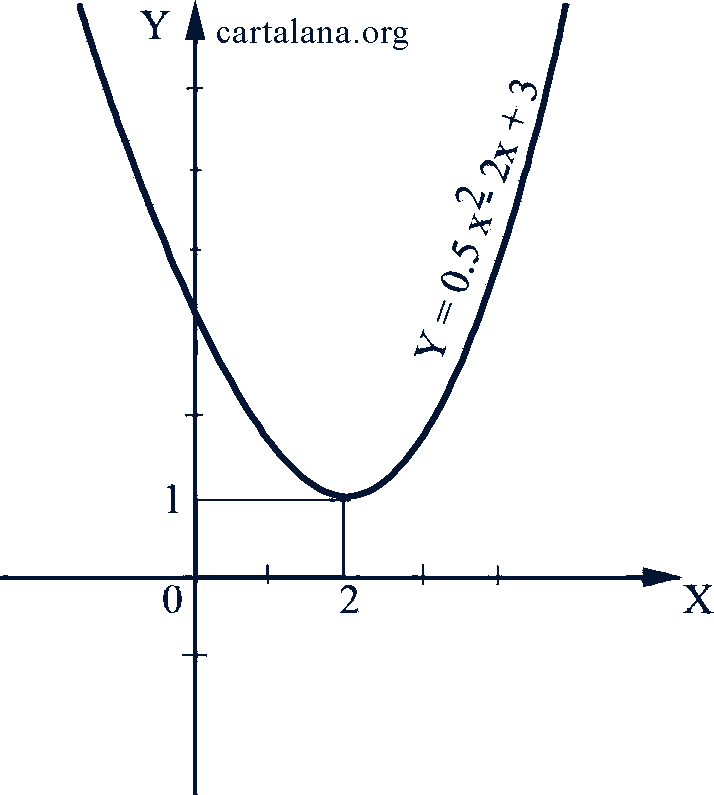
Рис. 43

Если дискриминант квадратного трехчлена 𝑎𝑥² + 𝑏𝑥 + 𝑐 отрицательный, т.е. 𝑏² - 4𝑎𝑐 < 0, то график функции 𝑦 = 𝑎𝑥² + 𝑏𝑥 + 𝑐 не пересекает ось абсцисс (рис. 44). Если он равен нулю, график функции касается оси абсцисс, причем точка касания есть корень уравнения 𝑎𝑥² + 𝑏𝑥 + 𝑐 = 0 (рис. 45). Если дискриминант положительный, парабола пересекает ось абсцисс в двух точках, являющихся корнями уравнения 𝑎𝑥² + 𝑏𝑥 + 𝑐 = 0 (рис. 46).

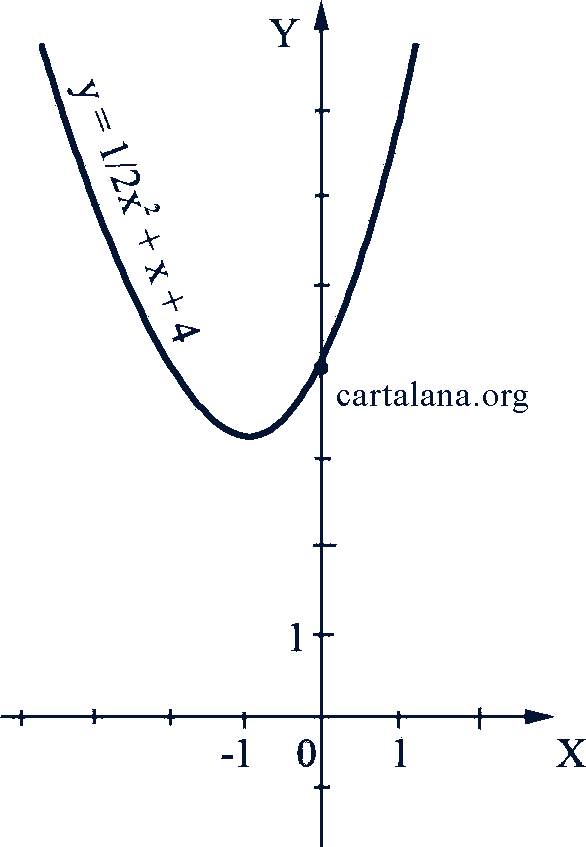
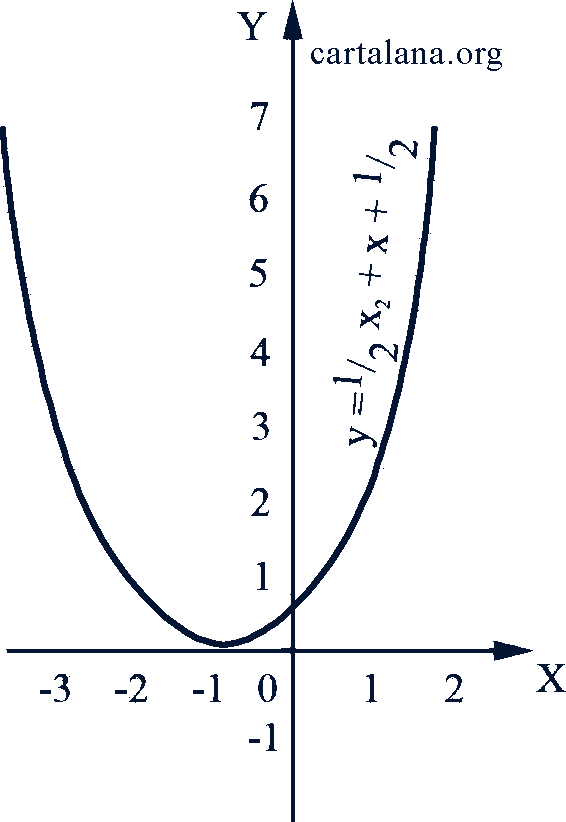
Рис. 44-45

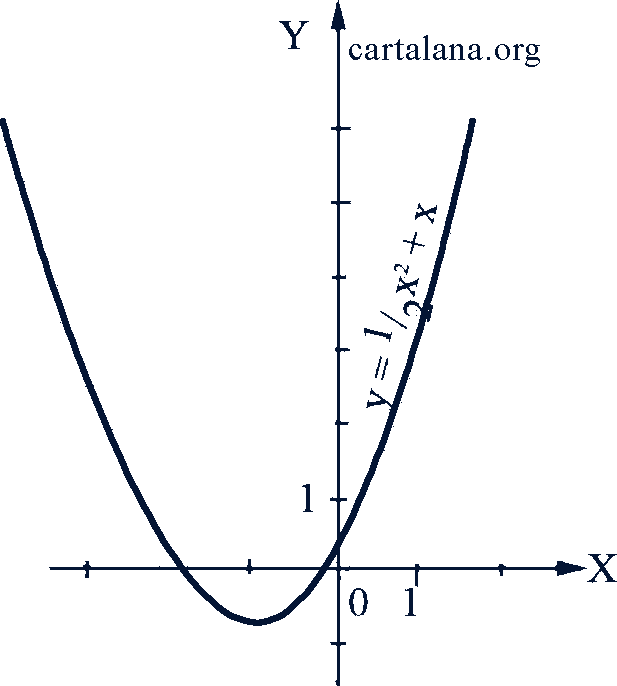
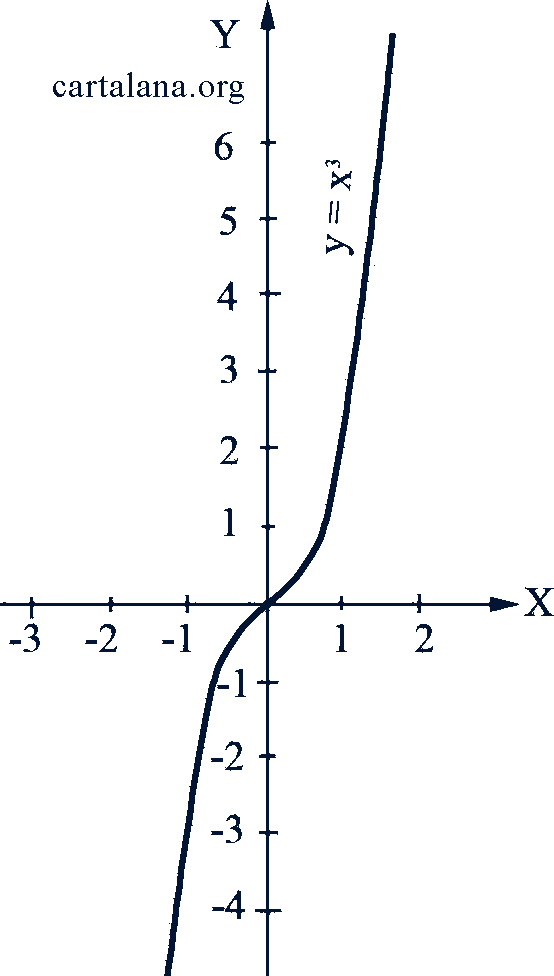
Рис. 46-47

5. Степенная функция. Степенной называют функцию, которую можно выразить формулой 𝑦 = 𝑥^𝑛, где 𝑥 - аргумент, а 𝑛 - показатель степени.

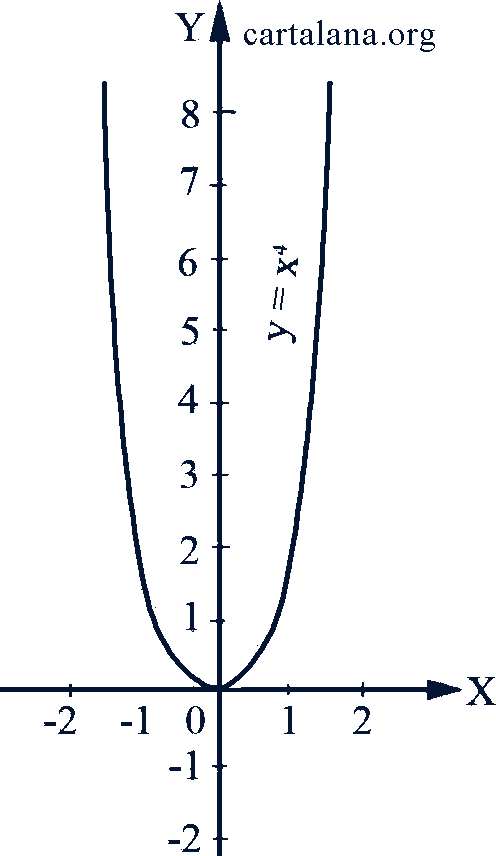
Рис. 48

При 𝑛, равном 1, 2, -1, имеем соответственно функции

𝑦 = 𝑥, 𝑦 = 𝑥² и ,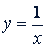

уже рассмотренные ранее.

Если 𝑛 - число целое четное, то функция 𝑦 = 𝑥^𝑛 четная; при нечетных 𝑛 она нечетная. При положительных 𝑛 эта функция определена для всех действительных значений аргумента 𝑥, при отрицательных 𝑛 она определена для всех 𝑥, кроме 𝑥 = 0. На рис. 47-50 даны графики степенной функции при показателях, соответственно равных 3, 4, -2, -3.

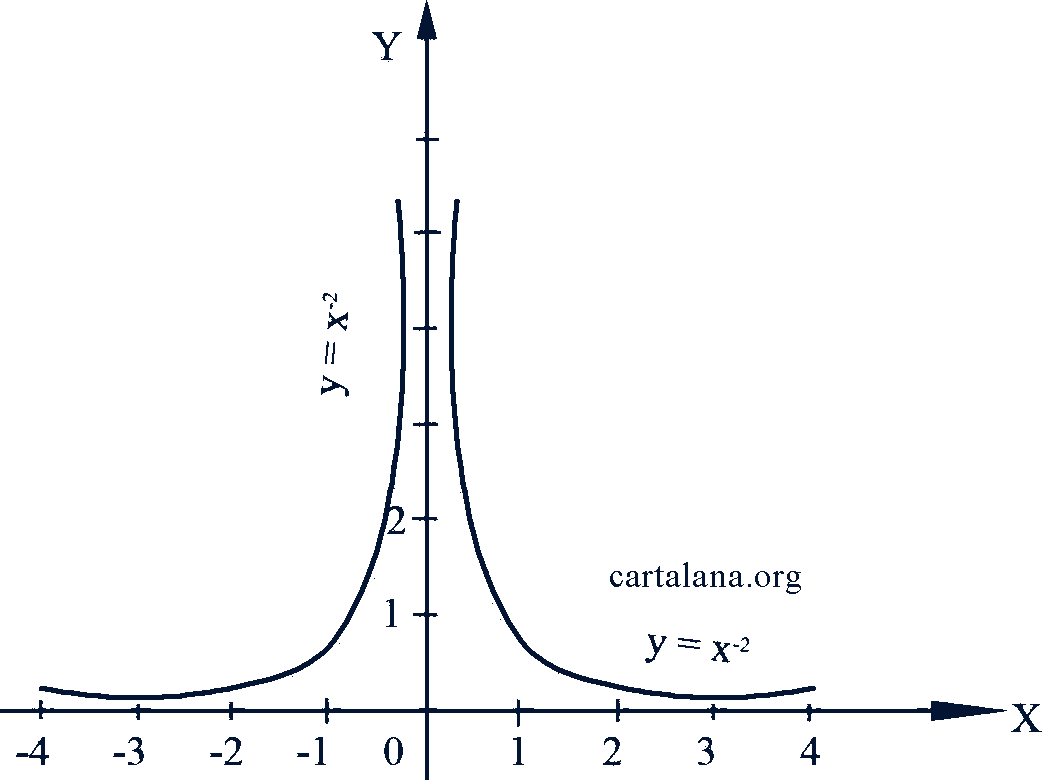
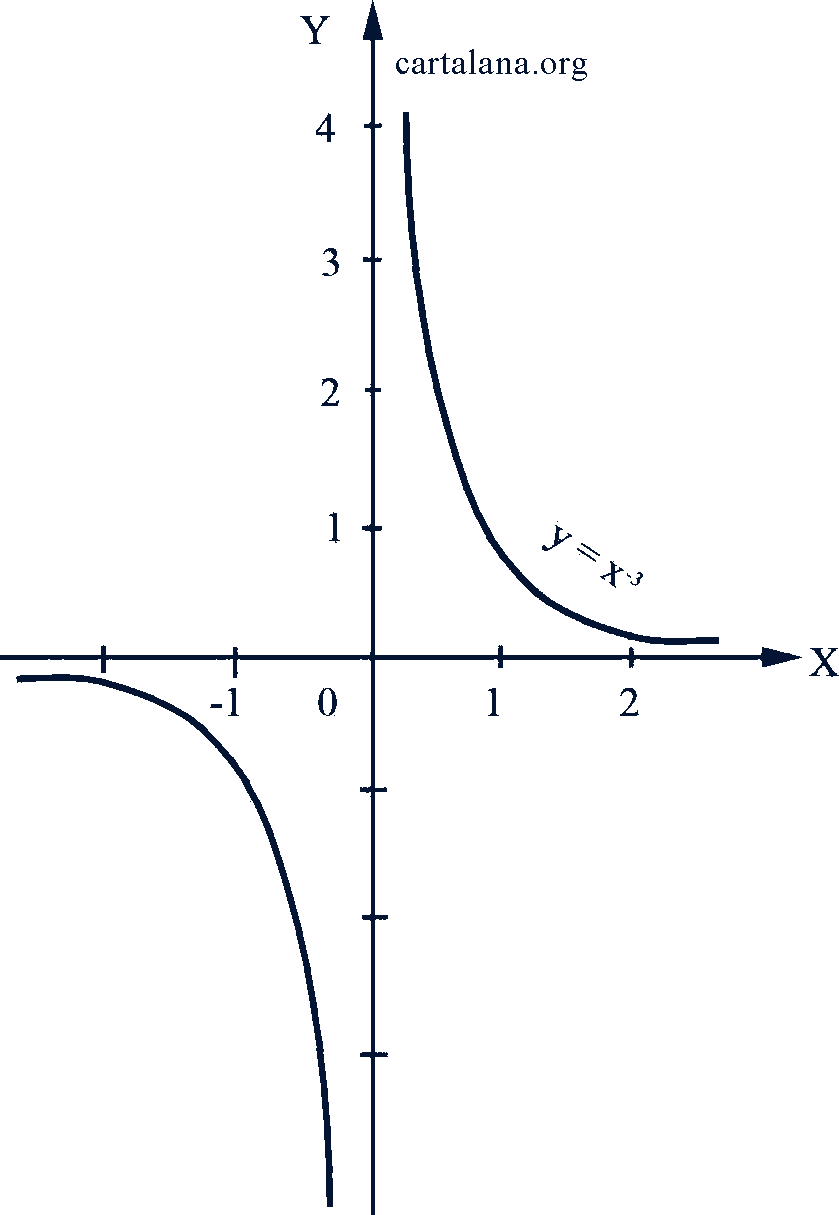
Рис. 49-50

Если 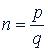- несократимая дробь, то при четном знаменателе 𝑞 функция 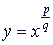определена только для положительных значений 𝑥. При нечетном знаменателе 𝑞 эта функция определена для всех значений 𝑥, если 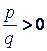; если же 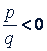, то она определена для всех 𝑥, кроме 𝑥 = 0. Если 𝑞 нечетное, то функция 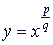четная при четном 𝑝 и нечетная при нечетном 𝑝.

На рис. 51-53 даны графики степенных функций при показателях соответственно .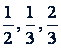

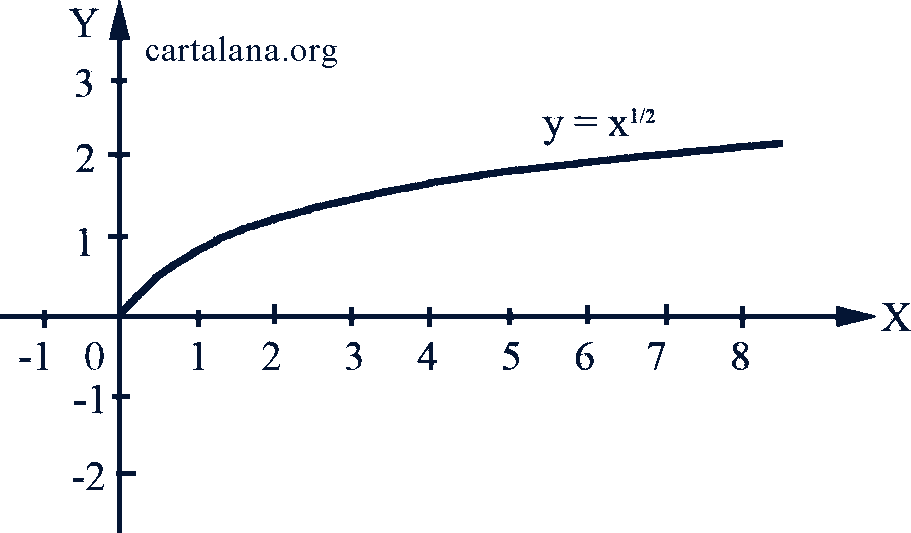
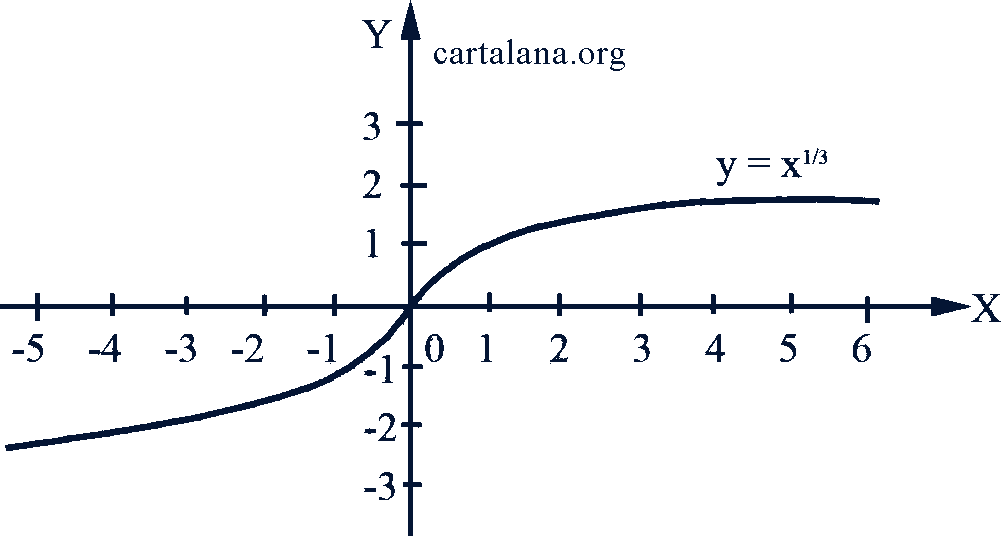
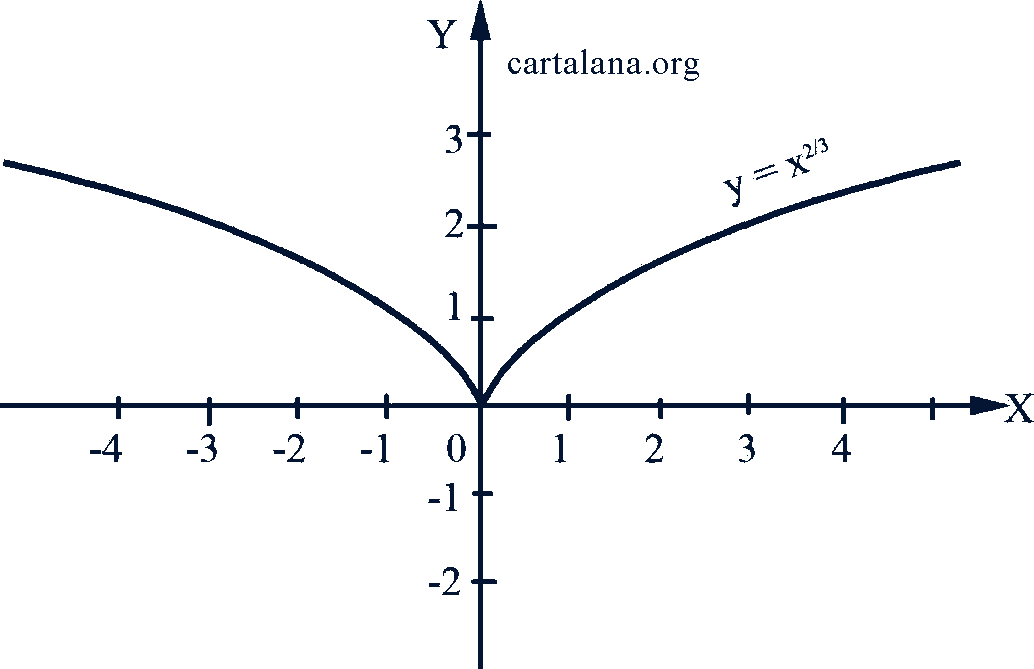
Рис. 51-52-53

При любом 𝑛 ≠ 0 степенная функция неограниченна, график каждой из этих функций проходит через точку (1, 1).

Если 𝑛 - число иррациональное, то функция 𝑦 = 𝑖^𝑛 определена только для положительных значений аргумента 𝑥 (или для неотрицательных 𝑥, если 𝑛 > 0).

6. Показательная функция. Функция, которую можно выразить формулой 𝑦 = 𝑎^𝑖, где 𝑥 - аргумент, a 𝑎 - положительное число, называется показательной функцией.

Эта функция определена для любых действительных 𝑥.

Примечание. Число 𝑎 здесь берется положительным потому, что при отрицательных 𝑎 числа 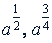и многие другие не были бы действительными. Если 𝑎 положительное, а 𝑥 равен несократимой дроби с четным знаменателем, то 𝑎^𝑖 имеет два действительных значения, например 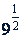имеет два значения: 3 и -3. Однако значения функции 𝑦 = 𝑎^𝑖 берутся только положительные: каждому действительному значению 𝑥 соответствует только одно положительное значение показательной функции 𝑎^𝑖.

Показательная функция при любом основании 𝑎 положительная. При 𝑎 > 1 эта функция возрастающая, а при 𝑎 < 1 - убывающая. График показательной функции - кривая, проходящая через точку (0, 1).

Он неограниченно приближается к оси абсцисс, но не достигает ее. Графики функций 𝑦 = 𝑎^𝑖 и 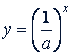симметричны относительно оси ординат.

На рис. 54 даны графики трех показательных функций:

𝑦 = 2^𝑖, 𝑦 = 0,5^𝑖 и 𝑦 = 5^𝑖.

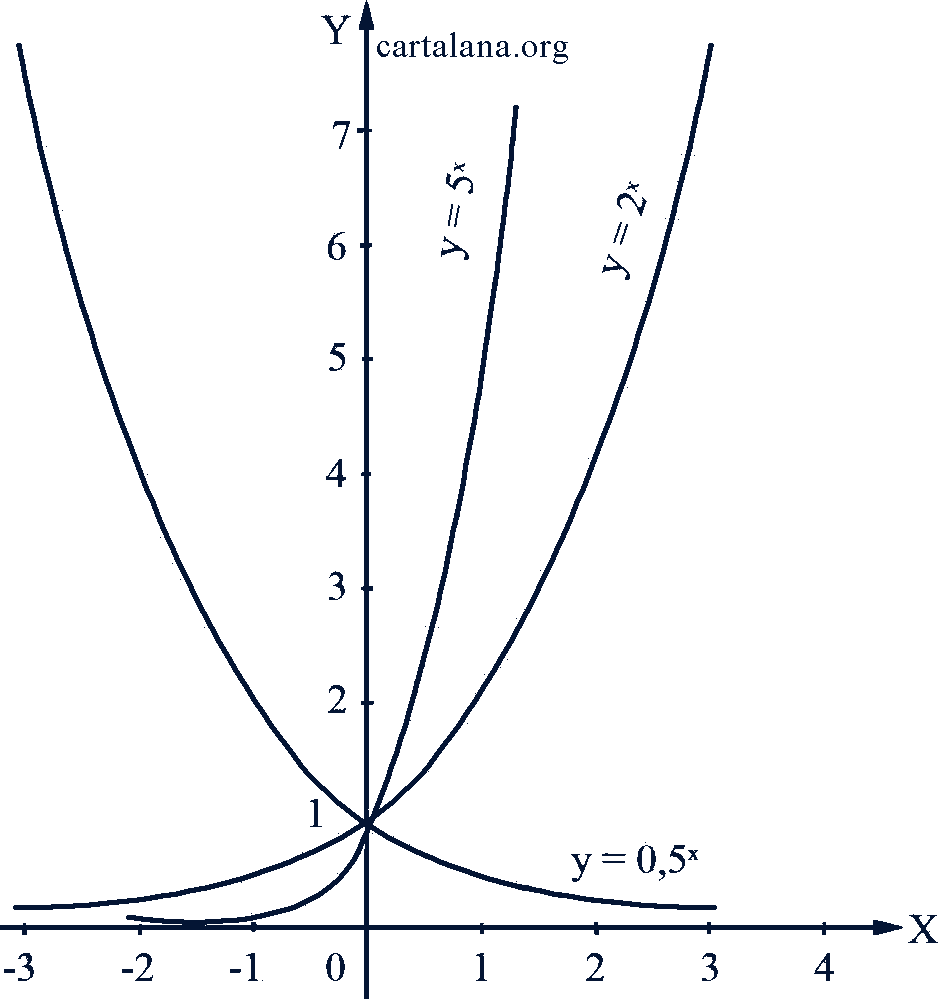
Рис. 54

33. Графические способы решения уравнений и неравенств

1. Системы уравнений с двумя неизвестными. С помощью графиков функций можно сравнительно легко находить (вообще говоря, приближенные) действительные решения систем двух уравнений с двумя неизвестными. Для этого каждое из уравнений рассматриваем как функциональную зависимость между его неизвестными, строим графики этих двух зависимостей на одной координатной плоскости и находим точку их пересечения. Абсцисса и ордината точки пересечения графиков дают решение системы.

Пример 1. Решить систему уравнений (графически)

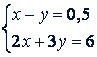
Решение. Каждое из этих уравнений линейное, следовательно их графики - прямые линии. Строим на одной координатной плоскости графики этих уравнений (рис. 55). Они пересекаются в одной точке с координатами 1,5 и 1.

Ответ. Данная система имеет одно решение: 𝑥 = 1,5, 𝑦 = 1.

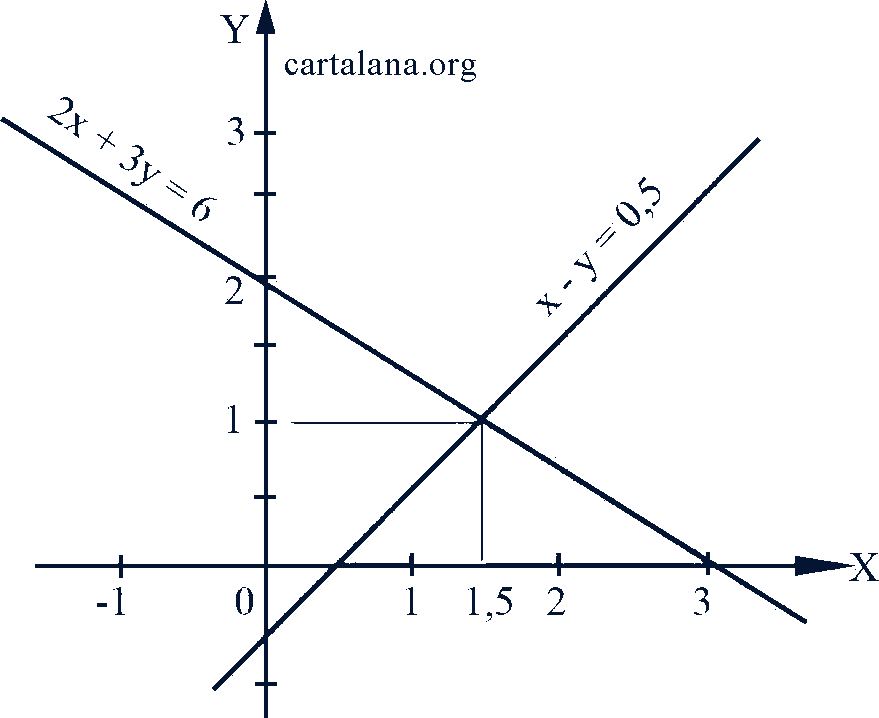
Рис. 55

Пример 2. Решить систему

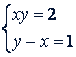
Решение. Данные уравнения можно преобразовать так:

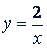и 𝑦 = 𝑖 + 1.

График первого уравнения есть гипербола, а второго - прямая (рис. 56). Они пересекаются в двух точках (1; 2) и (-2; -1).

Ответ. Система имеет два решения: 𝑥₁ = 1; 𝑦₁ = 2 и 𝑥₂ = -2; 𝑦₂ = -1.

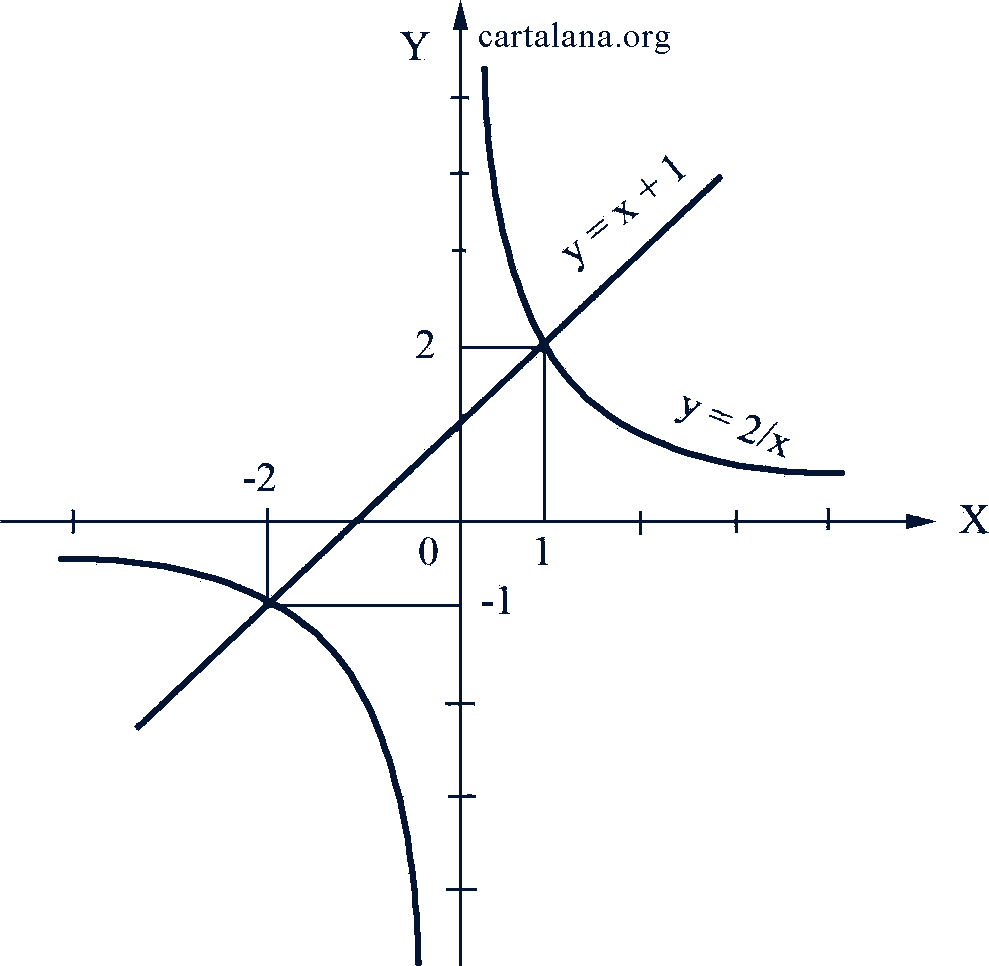
Рис. 56

2. Графическое решение уравнений с одним неизвестным.

Пример 1. Решить графическим способом уравнение

𝑥³ - 2𝑥 - 4 = 0.

Решение. Представим данное уравнение в виде

𝑥³ = 2𝑥 + 4.

Обозначим каждую его часть буквой 𝑦 и решим систему полученных двух уравнений с двумя неизвестными (рис. 57):

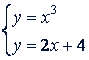
Как видим, графики пересекаются в одной точке с абсциссой 2.

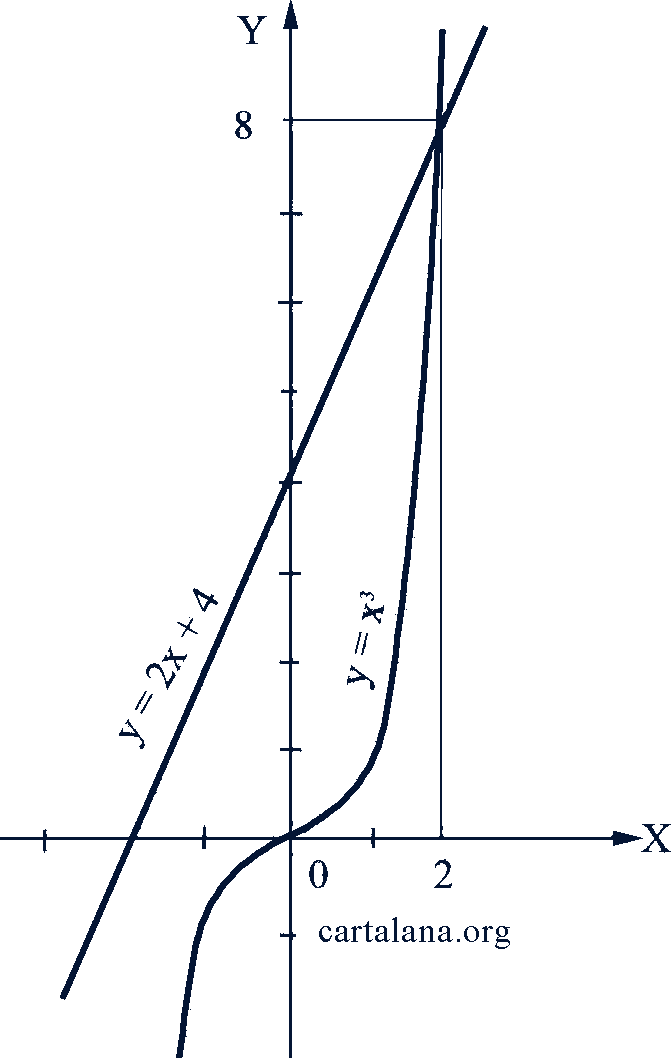
Рис. 57

Ответ. Данное уравнение имеет один действительный корень 𝑥 = 2.

Пример 2. Решить уравнение

𝑥⁴ - 𝑥 + 2 = 0.

Решение. 𝑥⁴ = 𝑥 - 2.

Рассмотрим систему

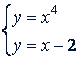
Построив графики каждого из уравнений (рис. 58), видим, что они не имеют общих точек.

Ответ. Данное уравнение действительных решений не имеет.

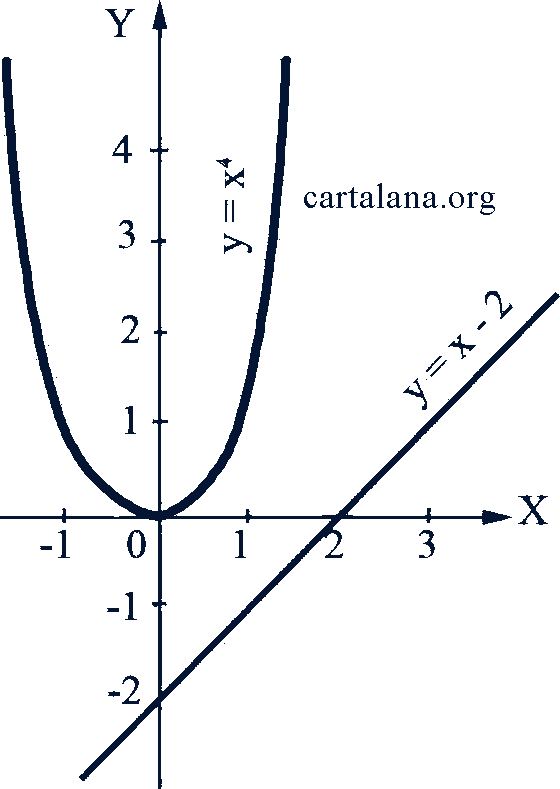
Рис. 58

3. Графическое решение неравенств с одним неизвестным.

Пример 1. Решить неравенство

𝑥² - 𝑥 - 2< 0.

Решение. Построив график функции 𝑦 = 𝑥² - 𝑥 - 2 (рис. 59), видим, что у отрицательный только при

-1< 𝑥 < 2.

Ответ. -1< 𝑥 < 2.

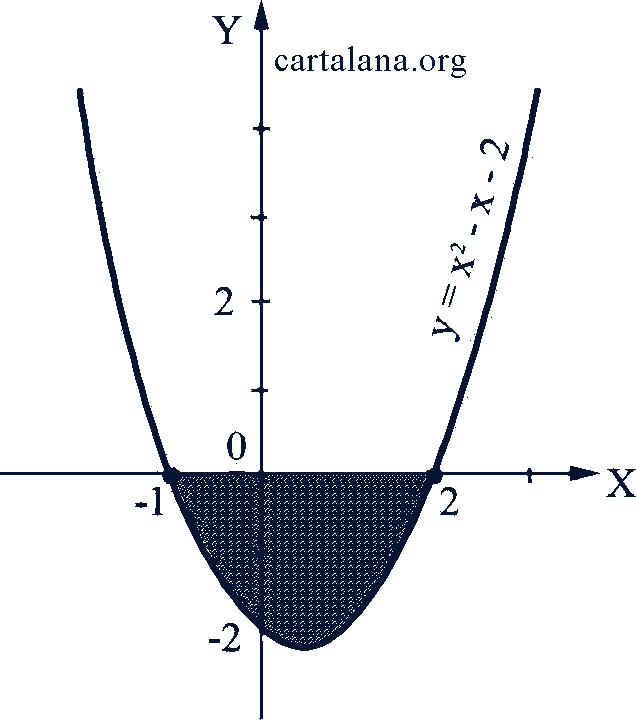
Рис. 59

Пример 2. Решить неравенство

2^{𝑖 +2}< 3𝑥 + 5.

Решение. Разделив обе части его на 4, получим 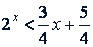. Обозначим 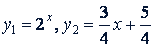и построим на одной координатной плоскости графики этих двух функций (рис. 60). Как видим, 𝑦₁ меньше соответствующего значения 𝑦₂ для 𝑥 из промежутка (-1; 1)

Ответ. -1 < 𝑥 < 1.

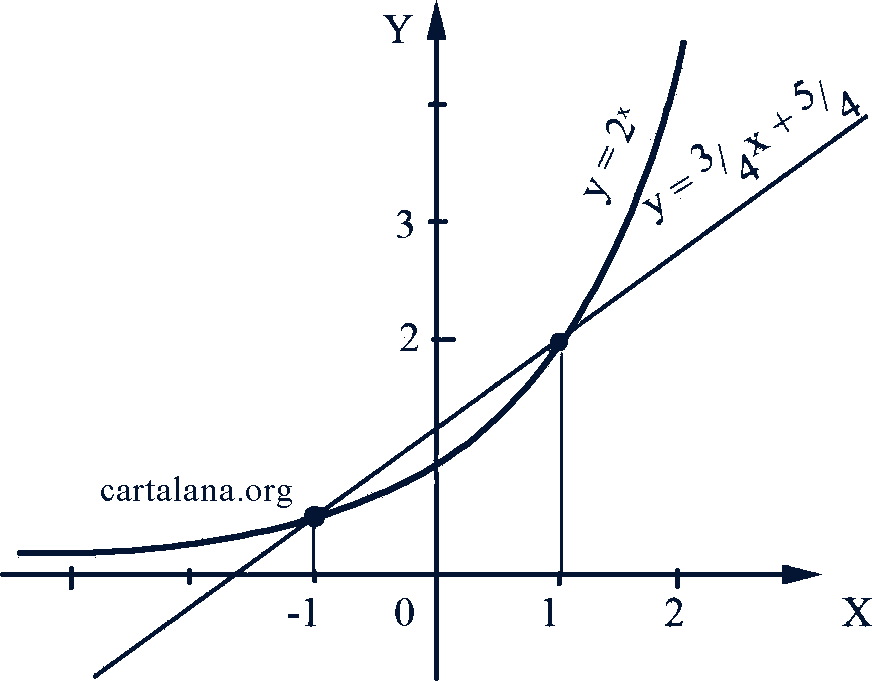
Рис. 60

34. Логарифмы

1. Определение логарифма. Логарифмом числа 𝑛 по данному основанию 𝑎 называется показатель степени 𝑥, в которую нужно возвести основание 𝑎, чтобы получить число 𝑛.

Обозначение: log_𝑎𝑛 = 𝑥. Таким образом, по определению, если 𝑥 = log_𝑎𝑛, то 𝑎^𝑥 = 𝑛, или 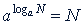. Основание 𝑎 предполагается положительным и не равным единице.

Примеры. log₂ 8 = 3, так как 2³ = 8; log₂ 0,25 = -2, так как 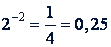. Знаком lg без указания основания обозначается десятичный логарифм, т.е., логарифм при основании 10, знаком log без указания основания - логарифм по произвольному основанию (в пределах одной формулы это основание мыслится одним и тем же) (Для теоретических исследований наиболее пригодным основанием логарифмов является иррациональное число 𝑒 = 2,71828183... (В высшей математике буквой 𝑒 обозначают 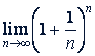. Логарифмы с основанием 𝑒 называются натуральными логарифмами. Их принято обозначать символом In. Например, In 𝑥 обозначает то же, что и log_𝑒 𝑥 ).

Логарифм - слово греческое, оно состоит из двух слов: λόγος - отношение, άριθμός - число. Слово "логарифм", таким образом, в буквальном переводе обозначает число, изменяющее отношение.

⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨

МЕНЮ САЙТА / СОДЕРЖАНИЕ