Ł Старые понятные учебники советских времен по физике, математике. Акупунктура, похудение

ШВЕЦОВ К.И., БЕВЗ Г.П."СПРАВОЧНИК ПО ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ. АРИФМЕТИКА, АЛГЕБРА", 1965

3. Система трех уравнений с тремя неизвестными. Система трех уравнений с тремя неизвестными имеет вид:

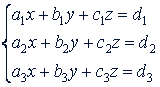
Здесь 𝑥, 𝑦, 𝑧 - неизвестные, а 𝑎¹ 𝑎², 𝑎³, 𝑏¹, 𝑏², 𝑏³, 𝑐¹, 𝑐², 𝑐³, 𝑑¹, 𝑑², 𝑑³ - данные числа.

Все свойства уравнений с одним и двумя неизвестными справедливы и для системы уравнений с тремя неизвестными. Поэтому для решения данной системы применимы те же способы, что и для системы двух уравнений с двумя неизвестными.

Пример 1. Решить систему

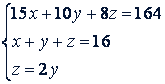
Решение. Исключаем 𝑥 из первого и второго уравнений данной системы (Эту систему нетрудно также решить, подставив в двух первых уравнениях вместо 𝑧 равное ему выражение 2𝑦 ). Для этого умножим обе части второго уравнения на 15:

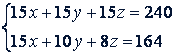
Коэффициенты при 𝑖 равны. Вычтя из первого уравнения второе, получим 5𝑦 + 7𝑧 = 76. Вместе с третьим уравнением оно дает систему уравнений с двумя неизвестными:

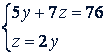
решив которую найдем: 𝑦 = 4, 𝑧 = 8.

Подставляя эти значения в уравнения первое или второе, получаем 𝑖 = 4. Следовательно, данная система трех уравнений с тремя неизвестными имеет единственное решение: 𝑥 = 4, 𝑦 = 4, 𝑧 = 8.

Пример 2. Решить систему

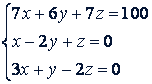
Решение. Умножим второе уравнение на 3 и прибавим его к первому:

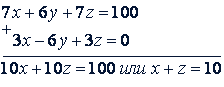
Умножим третье уравнение на 2 и прибавим ко второму:

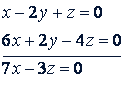
Полученные два уравнения, дают систему:

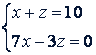
решив которую, найдем, 𝑥 = 3, 𝑧 = 7.

Подставляя значения 𝑥 и 𝑧 в третье уравнение системы, получаем:

9 + 𝑦 - 14 = 0, 𝑦 = 5.

Ответ. Система имеет единственное решение: 𝑖 = 3, 𝑦 = 5, 𝑧 = 7. В ряде частных случаев, учитывая специфические свойства данной системы, можно применять приемы, упрощающие процесс решения.

Пример 3. Решить систему

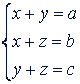
Решение. Складывая почленно все три уравнения и деля на 2, получаем

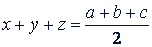
Вычитая из него последовательно третье, второе и первое уравнения, находим:

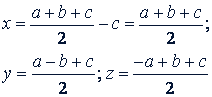
Пример 4. Решить систему

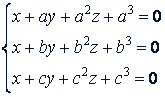
где 𝑎, 𝑏, 𝑐 - попарно различные числа.

Решение. Вычитая второе уравнение из первого, получаем:

(𝑎 - 𝑏) 𝑦 + (𝑎² - 𝑏²) 𝑧 + (𝑎³ - 𝑏³) = 0.

Сократим на 𝑎 - 𝑏 (так как 𝑎 ≠ 𝑏):

𝑦 + (𝑎 + 𝑏) 𝑧 + (𝑎² + 𝑎𝑏 + 𝑏²) = 0.

Аналогично, вычитая из первого уравнения третье, находим:

𝑦 + (𝑎 + 𝑐) 𝑧 + (𝑎² + 𝑎𝑐 + 𝑐²) = 0;

вычитая почленно полученные уравнения, исключаем 𝑦 :

(𝑏 - 𝑐) 𝑧 + (𝑎𝑏 - 𝑎𝑐 + 𝑏² - 𝑐²) = 0,

откуда 𝑧 = -(𝑎 + 𝑏 + 𝑐). Тогда из уравнения 𝑦 + (𝑎 + 𝑏) 𝑧 + (𝑎² + 𝑎𝑏 + 𝑏²) = 0 получим 𝑦 = 𝑎𝑏 + 𝑏𝑐 + 𝑎𝑐, и, наконец, воспользовавшись первым уравнением системы, найдем 𝑥 = - 𝑎𝑏𝑐.

4. Решение систем трех линейных уравнений с помощью определителей. Определителем третьего порядка, составленным из таблицы девяти чисел

𝑎¹, 𝑏¹, 𝑐¹,

𝑎², 𝑏², 𝑐²,

𝑎³, 𝑏³, 𝑐³,

называется число

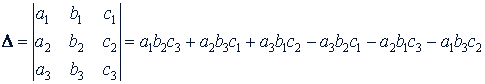
Вычисление определителей третьего порядка можно проводить по следующему правилу Саррюса. Дописав к данной таблице первый и второй столбцы, составим произведение элементов, находящихся на "главной диагонали" (рис. 21), а также элементов, находящихся на параллельных ей диагоналях, и возьмем эти произведения со своим знаком; составим произведение элементов, находящихся на "побочной диагонали", а также на параллельных ей диагоналях, и возьмем эти произведения с противоположным знаком. Алгебраическая сумма всех произведений равна Δ.

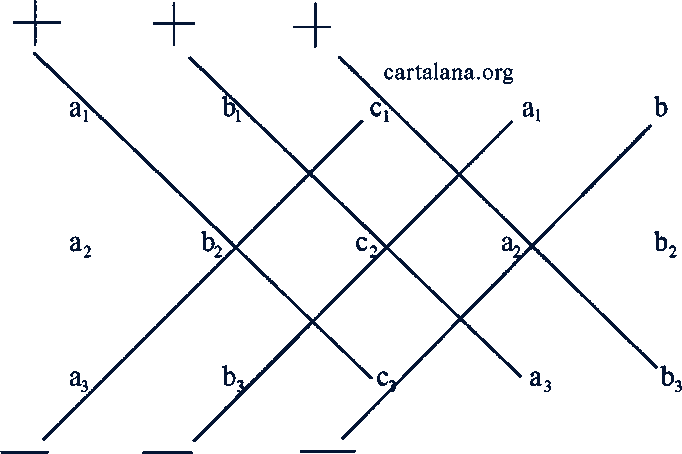
Рис. 21

Можно вычислить определитель с помощью правила, называющегося схемой треугольников (рис. 22). На левом рисунке соединены места таблицы, для которых произведения элементов следует взять со своим знаком. На правом рисунке соединены те места таблицы, для которых произведения элементов следует брать с противоположным знаком.

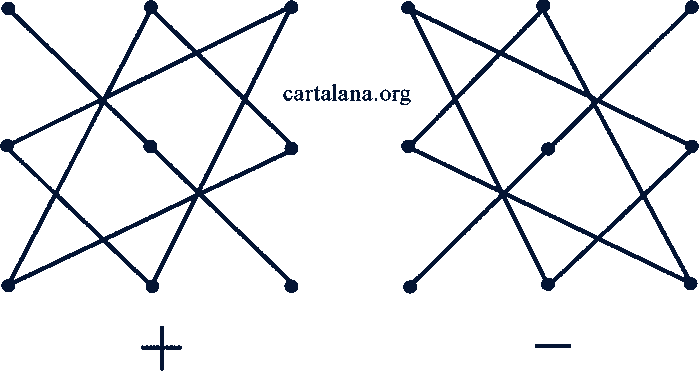
Рис. 22

Пример. Вычислить определитель

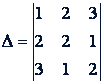
Решение. Согласно правилу Саррюса, имеем

Δ = 1 · 2 · 2 + 2 · 1 · 3 + 3 · 2 · 1 - 3 · 2 · 3 - 1 · 1 · 1 - 2 · 2 · 2 = -11

Теперь рассмотрим систему трех уравнений с тремя неизвестными

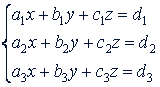
Если система имеет решение, то это решение представляется в удобном для запоминания виде:

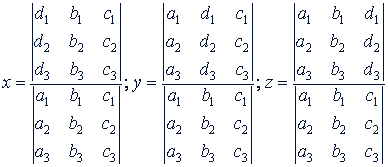
Обозначая определители, стоящие в числителе, соответственно через Δ¹, Δ², Δ³ и определитель, стоящий в знаменателе, через Δ (определитель системы уравнений), решение системы уравнений запишем так:

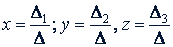
Эти равенства выражают правило Крамера для системы трех линейных уравнений с тремя неизвестными.

Пример. Решить систему

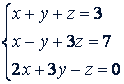
Решение.

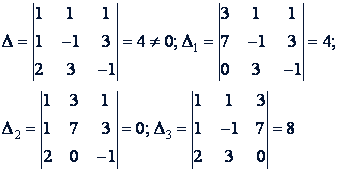
По правилу Крамера находим единственное решение системы:

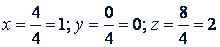
5. Исследование системы уравнений. Исследование системы производится в соответствии со следующими возможными случаями.

а) Δ ≠ 0. Система имеет единственное решение:

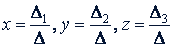
б) Δ = 0 и по крайней мере один из определителей Δ¹, Δ², Δ³ отличен от нуля. В этом случае система не имеет решений или имеет их бесконечное множество (Уточнения даются в курсах высшей алгебры, например Л.Я. Окунев, Высшая алгебра, Учпедгиз, 1958).

Пример. Исследовать систему

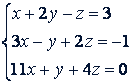
Решение.

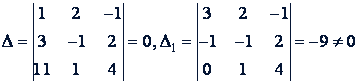
Ответ. Система не имеет решений.

Когда все коэффициенты при неизвестных равны нулю, то система противоречива, т.е. не имеет решений (если хотя бы один из свободных членов отличен от нуля) или удовлетворяется тождественно (если все свободные члены равны нулю).

6. Однородные системы. Система линейных уравнений называется однородной, если все свободные члены ее равны нулю. Однородная система трех уравнений с тремя неизвестными имеет вид:

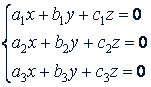
Однородная система не может быть противоречивой, так как она всегда имеет нулевое, или тривиальное, решение 𝑥 = 𝑦 = 𝑧 = 0. Чтобы система однородных уравнений допускала решения, отличные от тривиального, необходимо и достаточно, чтобы ее определитель был равен нулю.

21. Решение задач с помощью системы уравнений

Задача. На корм 8 лошадям и 15 коровам отпускали ежедневно 162 кг сена. Сколько сена ежедневно выдавали каждой лошади и каждой корове, если 5 лошадей съедали ежедневно сена на 3 кг больше, чем 7 коров?

Решение. Пусть для лошади отпускали ежедневно 𝑥 кг сена, а для коровы - 𝑦.

Тогда из первой части условия следует:

8𝑖 + 15𝑦 = 162, а из второй части условия - еще одно уравнение:

5𝑥 - 7𝑦 = 3.

Решим систему этих уравнений:

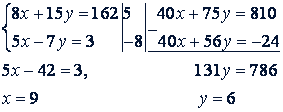
Ответ. 9 кг и 6 кг сена.

Задача. Латунь состоит из сплава меди и цинка. Кусок латуни весом 124 г при погружении в воду "потерял" 15 г. Сколько в нем содержится меди и цинка отдельно, если известно, что 89 г меди "теряют" в воде 10 г, а 7 г цинка - 1 г.

Решение. Пусть в латуни было 𝑥 граммов меди и 𝑦 граммов цинка. Тогда 𝑥 + 𝑦 = 124. Так как медь "теряет" 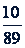своего веса, а цинк , то 𝑥 граммов меди потеряет 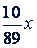, а 𝑦 граммов цинка 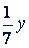. Следовательно, 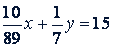. Решив систему уравнений, получим: 𝑥 = 89, 𝑦 = 35.

Ответ. 89 г меди и 35 г цинка.

Задача. Пароход прошел 100 км по течению реки и 64 км против течения за 9 ч. В другой раз за это время он прошел 80 км против течения и 80 км по течению реки. Определить скорость парохода в стоячей воде и скорость течения реки.

Указание. Скорость движения по течению равна сумме собственной скорости парохода и скорости течения. Скорость движения против течения равна разности между собственной скоростью парохода и скоростью течения.

Решение. Принимаем собственную скорость парохода в км/ч за 𝑥, а скорость течения за 𝑦.

Используем табличную запись решения.

Этапы	Направление движения	Путь (км)	Скорость (км/ч)	Время (ч)	Израсходовано времени
Первый	По течению Против течения	100 64	𝑥 + 𝑦 𝑖 - 𝑦		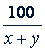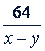9 ч
Второй	Против течения По течению	80 80	𝑥 - 𝑦 𝑖 + 𝑦		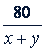9 ч

Имеем систему

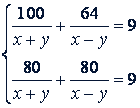
Это не линейная система, но способом замены ее можно привести к линейной. Обозначим

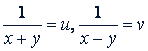
Тогда получим

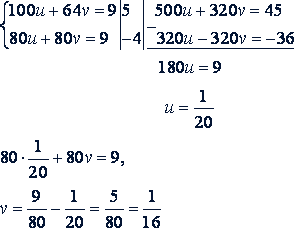
Следовательно,

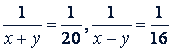
или

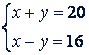
Решив эту систему, получим: 𝑥 = 18, 𝑦 = 2. Ответ. 18 км/ч и 2 км/ч.

⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨

МЕНЮ САЙТА / СОДЕРЖАНИЕ