Я создала и активно наполняю телеграм-канал "Перець". Здесь лучшие карикатуры из журнала, начиная с 1922 года.
Заходите, подписывайтесь: https://t.me/cartalana

ШВЕЦОВ К.И., БЕВЗ Г.П."СПРАВОЧНИК ПО ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ. АРИФМЕТИКА, АЛГЕБРА", 1965

МЕНЮ САЙТА / СОДЕРЖАНИЕ

23. Основные типы задач на проценты

1. Нахождение процентов данного числа

Задача. Бригада трактористов по плану должна израсходовать 9 т горючего. Трактористы взяли соцобязательство сэкономить 20% горючего. Определить экономию горючего в тоннах.

Если в этой задаче вместо 20% написать равное ему число 0,2, получим задачу, на нахождение дроби числа. А такие задачи решают умножением. Отсюда вытекает способ решения:

20% = 0,2; 9 · 0,2 = 1,8 (𝑚).

Вычисления можно записать и так:

(𝑚)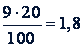

Вообще, 𝑝 % числа 𝑎 равны .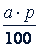

Чтобы найти несколько процентов данного числа, достаточно данное число разделить на 100 и умножить результат на число процентов.

Задача. Рабочий в 1963 г. получал в месяц 90 руб., а в 1964 г. стал получать на 30% больше. Сколько получал он в 1964 г.?

Решение (первый способ).

1) На сколько рублей больше стал получать рабочий?

(руб.)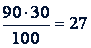

2) Какова была месячная зарплата рабочего в 1964 г.?

90 + 27 = 117 (руб).

Второй способ.

1) Сколько процентов прежнего заработка стал получать рабочий в 1964 г.?

100% + 30% = 130%.

2) Какова была месячная зарплата рабочего в 1964 г.?

(руб.)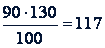

2. Нахождение числа по данной величине его процентов.

Задача. В колхозе посеяли кукурузу на площади 280 га, что составляет 14% всей посевной площади. Определить посевную площадь колхоза.

Если в этой задаче вместо 14% написать 0,14 или 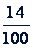, то получим задачу на нахождение числа по известной величине его дроби. А такие задачи решают делением.

Решение. 14% = 0,14; 280 : 0,14 = 2000 (га). Можно это решение оформить и так:

(га)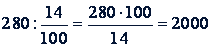

Вообще, если 𝑝 % какого-то числа составляет 𝑎, то все число равно .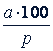

Чтобы найти число по данной величине нескольких процентов его, достаточно эту величину разделить на число процентов и результат умножить на 100.

Задача. В марте завод выплавил 125,4 т. металла, перевыполнив план на 4,5%. Сколько тонн металла завод должен был выплавить в марте по плану?

Решение.

1) На сколько процентов завод выполнил план в марте?

100% + 4,5% = 104,5%.

2) Сколько тонн металла завод должен был выплавить?

(га)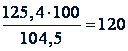

3. Нахождение процентного отношения двух чисел.

Задача. Нужно вспахать 300 га земли. В первый день вспахали 120 га. Сколько процентов к заданию вспахали в первый день?

Решение.

Первый способ. 300 га составляет 100%, значит, на 1% приходится 3 га. Определив, сколько раз 3 га, составляющие 1%, содержатся в 120 га, мы узнаем сколько процентов к заданию вспахали земли в первый день

120 : 3 = 40(%).

Второй способ. Определив, какую часть земли вспахали в первый день, выразим эту дробь в процентах.

Записываем вычисление:

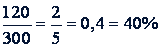
Чтобы вычислить процентное отношение числа 𝑎 к числу 𝑏, нужно найти отношение 𝑎 к 𝑏 и умножить его на 100.

Задача. Автомобиль на каждые 100 км пути летом расходует 8 л бензина, а зимой 8,8 л. На сколько процентов зимняя норма больше летней?

Решение. Зимой на каждые 100 км автомобиль расходует на 8,8 - 8 = 0,8 (л) больше, чем летом. Эти 0,8 л по отношению к 8 л составляют 0,8 : 8 = 0,1 = 10%.

Ответ. На 10%.

Примечание. Иногда учащиеся считают, что в данном случае летняя норма расхода бензина меньше зимней также на 10%. Это неверно. В первом случае, когда мы сравниваем расход бензина с летней нормой, мы принимаем за 100% 8 л, если же сравнивать с зимней нормой, нужно за 100% принимать 8,8 л, и ту же разность 0,8 d делить уже не на 8 л, а на 8,8 л, т.е.

0,8 : 8,8 = 0,091 = 9,1%.

Как видим, летняя норма меньше зимней не на 10%, а на 9,1%.

4. Таблицы процентных отношений. Задачи на нахождение процентного отношения чисел широко распространены на практике. Для облегчения вычислений и экономии времени составлены таблицы процентных отношений.

В приведенной части таблицы можно найти процентные отношения чисел от 61 до 70 к числам от 61 до 70. Найдем, например, чему равно процентное отношение 62 к 64. Во второй строке первого столбца найдем число 62; на пересечении этой строки и столбца с числом 64 найдем процентное отношение 62 к 64. Оно равно 96,88%.

Воспользуемся теперь нашей таблицей для решения такой задачи.

Для отопления дома необходимо заготовить 70 т угля. На 1 октября привезено 65 т. Сколько процентов топлива заготовлено?

Решение задачи состоит в нахождении процентного отношения 65 к 70. Это отношение ищем по таблице, оно равно 92,86%.

5. График для решения задач на проценты. С помощью простого графика (рис. 7) можно решать задачи на проценты. Искомые и данные числа откладывают на отрезках 𝐴𝐵 и 𝐵𝐶. На графике показано, как при помощи линейки найти 80% от 50, а также, что число 40 составляет 80% от 50 (обратная задача).

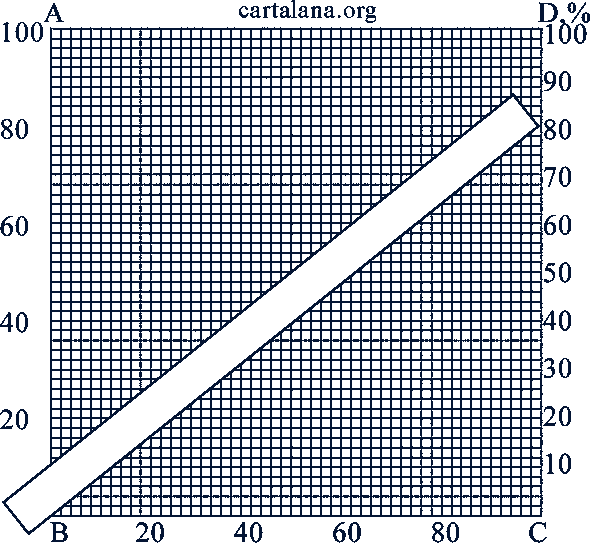
Рис. 7

24. Приближенные вычисления

1. Числа точные и приближенные. Числа, с которыми мы встречаемся на практике, бывают двух родов. Одни дают истинное значение величины, другие - только приблизительное. Первые называют точными, вторые - приближенными. Чаще всего удобно пользоваться приближенным числом вместо точного, тем более, что во многих случаях точное число вообще найти невозможно.

Так, если говорят, что в классе есть 29 учеников, то число 29 - точное. Если же говорят, что расстояние от Москвы до Киева равно 960 км, то здесь число 960 - приближенное, так как, с одной стороны, наши измерительные инструменты не абсолютно точны, с другой стороны, сами города имеют некоторую протяженность.

Результат действий с приближенными числами есть тоже приближенное число. Выполняя некоторые действия над точными числами (деление, извлечение корня), можно также получить приближенные числа.

Теория приближенных вычислений позволяет: 1) зная степень точности данных, оценить степень точности результатов; 2) брать данные с надлежащей степенью точности, достаточной для обеспечения требуемой точности результата; 3) рационализировать процесс вычисления, освободив его от тех выкладок, которые не окажут влияния на точность результата.

2. Округление. Одним из источников получения приближенных чисел является округление. Округляют как приближенные, так и точные числа.

Округлением данного числа до некоторого его разряда называют замену его новым числом, которое получается из данного путем отбрасывания всех его цифр, записанных правее цифры этого разряда, или путем замены их нулями. Эти нули обычно подчеркивают или пишут их меньшими. Для обеспечения наибольшей близости округленного числа к округляемому следует пользоваться такими правилами: чтобы округлить число до единицы определенного разряда, надо отбросить все цифры, стоящие после цифры этого разряда, а в целом числе заменить их нулями. При этом учитывают следующее:

1) если первая (слева) из отбрасываемых цифр менее 5, то последнюю оставленную цифру не изменяют (округление с недостатком);

2) если первая отбрасываемая цифра больше 5 или равна 5, то последнюю оставленную цифру увеличивают на единицу (округление с избытком).

Покажем это на примерах. Округлить:

а) до десятых 12,34;

б) до сотых 3,2465; 1038,785;

в) до тысячных 3,4335.

г) до тысяч 12375; 320729.

Ответы.

а) 12,34 ≈ 12,3;

б) 3,2465 ≈ 3,25; 1038,785 ≈ 1038,79;

в) 3,4335 ≈ 3,434.

г) 12375 ≈ 12 000; 320729 ≈ 321000.

Примечание. Еще Несколько лет назад в случае отбрасывания одной лишь цифры 5 пользовались "правилом четной цифры": последнюю цифру оставляли без изменения, если она четная, и увеличивали на единицу, если нечетная. Теперь же "правила четной цифры" не придерживаются: если отбрасывают одну цифру 5, то к последней оставленной цифре прибавляют единицу независимо от того, четная она или нечетная.

3. Абсолютная и относительная погрешности. Разность между точным числом и его приближенным значением называется абсолютной погрешностью приближенного числа. Например, если точное число 1,214 округлить до десятых, получим приближенное число 1,2. В данном случае абсолютная погрешность приближенного числа 1,2 равна 1,214 - 1,2, т.е. 0,014.

Но в большинстве случаев точное значение рассматриваемой величины неизвестно, а только приближенное. Тогда и абсолютная погрешность неизвестна. В этих случаях указывают границу, которую она не превышает. Это число называют граничной абсолютной погрешностью. Говорят, что точное значение числа равно его приближенному значению с погрешностью меньшей, чем граничная погрешность. Например, число 23,71 есть приближенное значение числа 23,7125 с точностью до 0,01, так как абсолютная погрешность приближения равна 0,0025 и меньше 0,01. Здесь граничная абсолютная погрешность равна 0,01 (Абсолютная погрешность бывает и положительной и отрицательной. Например, 1,68 ≈ 1,7. Абсолютная погрешность равна 1,68–1,7 ≈ –0,02. Граничная абсолютная погрешность всегда положительна).

Граничную абсолютную погрешность приближенного числа 𝑎 обозначают символом Δ𝑎. Запись

𝑖 ≈ 𝑎 (±Δ 𝑎)

следует понимать так: точное значение величины 𝑖 находится в промежутке между числами 𝑎–Δ𝑎 и 𝑎 + Δ 𝑎, которые называют соответственно нижней и верхней границей 𝑥 и обозначают НГ 𝑖 ВГ 𝑥.

Например, если 𝑖 ≈ 2,3(±0,1), то 2,2 < 𝑖 < 2,4.

Наоборот, если 7,3 < 𝑥 < 7,4, то 𝑥 ≈ 7,35 (±0,05). Абсолютная или граничная абсолютная погрешность не характеризует качество выполненного измерения. Одна и та же абсолютная погрешность может считаться значительной и незначительной в зависимости от числа, которым выражается измеряемая величина. Например если измеряем расстояние между двумя городами с точностью до одного километра, то такая точность вполне достаточна для этого изменения в то же время при измерении расстояния между двумя домами одной улицы такая точность будет недопустимой. Следовательно, точность приближенного значения величины зависит не только от величины абсолютной погрешности, но и от значения измеряемой величины. Поэтому мерой точности служит относительная погрешность.

Относительной погрешностью называется отношение абсолютной погрешности к величине приближенного числа. Отношение граничной абсолютной погрешности к приближенному числу называют граничной относительной погрешностью; обозначают ее так: 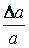. Относительную и граничную относительную погрешности принято выражать в процентах. Например, если измерения показали, что расстояние 𝑥 между двумя пунктами больше 12,3 км, но меньше 12,7 км, то за приближенное значение его принимают среднее арифметическое этих двух чисел, т.е. их полусумму, тогда граничная абсолютная погрешность равна полуразности этих чисел. В данном случае 𝑥 ≈ 12,5 (±0,2). Здесь граничная абсолютная погрешность равна 0,2 км, а граничная относительная

.

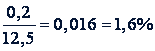⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨

МЕНЮ САЙТА / СОДЕРЖАНИЕ