
Я создала и активно наполняю телеграм-канал "Перець". Здесь лучшие карикатуры из журнала, начиная с 1922 года.
Заходите, подписывайтесь: https://t.me/cartalana

ЧЕРТОВ А.Г. "ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН", 1977
Таблица 10. Рационализованные (СИ) и нерационализованные (система СГС) уравнения электромагнитного поля *
| Величина или физический закон | СИ | СГС |
| Закон Кулона | 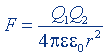 | 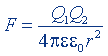 |
| Напряженность электрического поля точечного заряда | 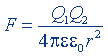 | 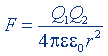 |
| Поток вектора напряженности | 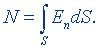 | |
| Теорема Остроградского - Гаусса для потока вектора напряженности | 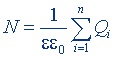 | 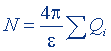 |
| Напряженность электрического поля бесконечно длинной заряженной нити | 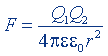 | 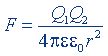 |
| То же, заряженной сферической поверхности (для r ⋝ R) | 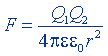 | 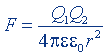 |
| То же, бесконечной заряженной плоскости | 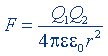 | 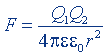 |
| То же, плоского конденсатора | 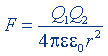 | 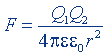 |
| Сила, действующая на заряд в электрическом поле | 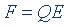 | |
| Электрический момент диполя | 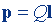 | |
| Напряженность электрического поля диполя | 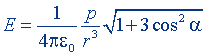 | 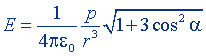 |
| Механический момент, действующий на диполь в электрическом поле | 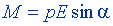 | |
| Электрическое смещение | D = εε0E | D = εE |
| Поток вектора электрического смещения | 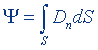 | |
| Теорема Остроградского - Гаусса для потока электрического смещения | 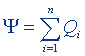 | 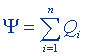 |
| Электрическая емкость | 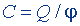 | |
| То же, уединенной проводящей сферы | C = 4πεε0r | C = εr |
| То же, плоского конденсатора | 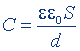 | 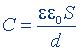 |
| То же, цилиндрического конденсатора | 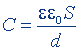 | 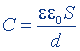 |
| То же, сферического конденсатора | 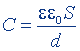 | 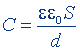 |
| Поляризованность (вектор поляризации) | 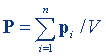 | |
| Связь поляризованности с напряженностью результирующего поля в диэлектрике | Р = kеε0Е | P = keE |
| Связь между диэлектрической проницаемостью и электрической восприимчивостью | ε = 1 + kе | ε = 1 + 4πke |
| Связь между векторами D, Е и Р | D = ε0E + Р | D = E + 4πР |
| Зависимость электрического момента неполярной молекулы диэлектрика от напряженности внешнего поля и поляризуемости β молекулы | p = ε0βЕ | p = βE |
| Потенциал поля точечного заряда | 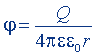 | 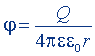 |
| То же, диполя | 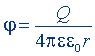 | 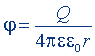 |
| Работа перемещения заряда в электрическом поле | 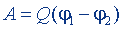 | |
| Связь между напряженностью и потенциалом электрического поля в общем случае |  | |
| То же, в случае однородного поля | 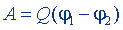 | |
| Циркуляция вектора напряженности электрического поля | 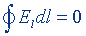 | |
| Энергия системы точечных зарядов | 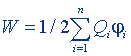 | |
| То же, заряженного проводника | 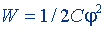 | |
| То же, поля конденсатора | 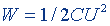 | |
| Объемная плотность энергии электрического поля | 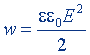 | 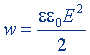 |
| Закон Био - Савара - Лапласа | 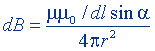 | 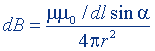 |
| Магнитная индукция поля прямого тока | 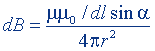 | 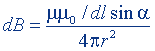 |
| То же, в центре кругового тока | 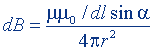 | 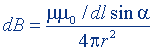 |
| То же, на оси соленоида | В = μμ0nI | 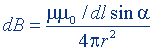 |
| То же, поля движущегося заряда | 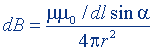 | 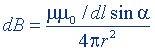 |
| Закон Ампера | dF = BI sin α dl | 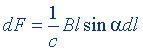 |
| Сила взаимодействия двух бесконечно длинных параллельных токов | 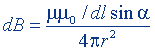 | 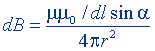 |
| Магнитный момент контура с током | pm = IS | 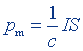 |
| Механический момент, действующий на контур с током в однородном магнитном поле | 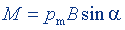 | |
| Сила Лоренца | F = QvB sin α | 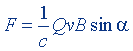 |
| Магнитный поток | 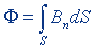 | |
| Работа по перемещению проводника с током в магнитном поле | А = IΔ Ф | 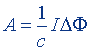 |
| Потокосцепление | 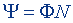 | |
| Ψ = LI | 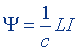 | |
| Индуктивность соленоида | L = μμ0n2V | L = 4πμn2V |
| Закон Фарадея - Максвелла | Ɛi = -dΨ/dt | Ɛi = -1/c·dΨ/dt |
| Электродвижущая сила самоиндукции | Ɛi = -LdI/dt | Ɛi = -1/c2·LdI/dt |
| Сила тока замыкания | 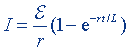 | 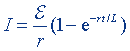 |
| Сила тока размыкания | 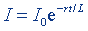 | 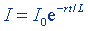 |
| Заряд, протекающий в контуре при изменении магнитного потока, пронизывающего контур | 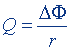 | 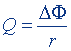 |
| Связь между магнитной индукцией и напряженностью магнитного поля | В = μμ0H | В = μH |
| Энергия магнитного поля соленоида | 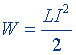 | 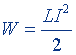 |
| Плотность энергии магнитного поля | 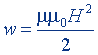 | 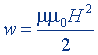 |
| Магнитный поток в неразветвленной цепи (формула Гопкинсона) | 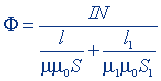 | 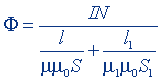 |
| Циркуляция вектора напряженности магнитного поля | 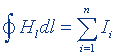 | 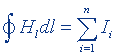 |
| Магнитодвижущая сила | F = IN | F = 1/c·4πIN |
| Намагниченность магнетика | 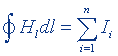 | |
| Связь намагниченности с напряженностью внешнего магнитного поля | J = kmH | |
| Связь между векторами В, Н и J в магнетике | B =μ0H + μ0J | В = H + 4πJ |
| Связь между магнитной проницаемостью и магнитной восприимчивостью | μ = 1 + km | μ = 1 + 4πkm |
| Магнитная индукция внутреннего поля, обусловленного ориентацией элементарных магнитных моментов | Bʹ = μ0J | Вʹ = 4πJ |
| Формула Томсона | 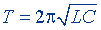 | 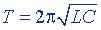 |
| Связь электрической и магнитной постоянных | 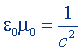 | ε0μ0 = 1 |
| Скорость распространения электромагнитных волн в среде | 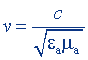 | |
| Вектор Пойнтинга | S = [FH] | 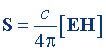 |
| Плотность тока смещения | δсм = dD/dt | 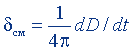 |
| Уравнения Максвелла в интегральной форме | 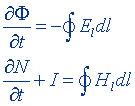 | 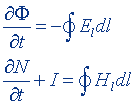 |
| Уравнения Максвелла в дифференциальной форме (полная система уравнений электромагнитного поля) | 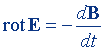 | 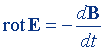 |
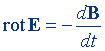 | 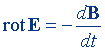 | |
| div D = ρ | div D = 4πρ | |
 | ||
| D = εε0E | D = εE | |
| В = μμ0Н | B = μH | |
 | ||
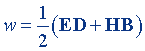 |  | |
* Уравнения, имеющие одинаковый вид в рационализованной и нерационализованной формах, записаны в таблице один раз и заключены в рамку.
⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨
МЕНЮ САЙТА / СОДЕРЖАНИЕ
∎ cartalana.comⒸ 2009-2025
∎ контакт: cartalana@cartalana.
com ∎