
Я создала и активно наполняю телеграм-канал "Перець". Здесь лучшие карикатуры из журнала, начиная с 1922 года.
Заходите, подписывайтесь: https://t.me/cartalana

ЧЕРТОВ А.Г. "ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН", 1977
§ 28. СООТНОШЕНИЯ ЕДИНИЦ МЕЖДУНАРОДНОЙ СИСТЕМЫ С ЕДИНИЦАМИ СИСТЕМЫ СГС И ВНЕСИСТЕМНЫМИ ЕДИНИЦАМИ
При вычислении физических величин при помощи расчетных формул когерентной системы все величины, входящие в формулу, необходимо выражать в единицах одной системы. Невыполнение этого правила приводит к ошибке. Но так как в условиях физических задач величины могут быть выражены в единицах разных систем и во внесистемных единицах, то часто возникает необходимость в переводе числовых значений физических величин из одной системы в другую. Рассмотрим, каким образом можно получить соотношения между единицами однородных величин в разных системах.
Чтобы выразить производную единицу одной системы (А) в единицах другой системы (В), необходимо выполнить следующие действия:
а) выразить производную единицу системы А через ее основные единицы;
б) входящие в данную производную единицу основные единицы системы А выразить в соответствующих единицах системы В (предполагается, что соотношение основных единиц системы А с однородными единицами системы В нам известно);
в) в полученном выражении произвести алгебраические действия как с числами, так и наименованиями основных единиц системы В;
г) если же переводимая производная единица системы A выражается через другие производные единицы той же системы, соотношение которых с соответствующими единицами системы В известно, то достаточно выразить переводимую единицу через производные единицы этой же системы, а затем последние - через соответствующие единицы системы В и выполнить алгебраические действия.
Пользуясь этими правилами, получим соотношения между некоторыми однородными единицами. Учитывая, что с введением Международной системы расчеты должны производиться главным образом с применением единиц этой системы, рассмотрим примеры перевода единиц системы СГС и внесистемных единиц в единицы СИ.
Пример 1. Выразить единицу силы СГС - дину в ньютонах.
В соответствии с указанными выше правилами выполним действий
а) выразим дину через сантиметр, грамм, секунду:
1 дин = 1 г·см/с2;
б) выразим сантиметр и грамм, входящие в размерность дины, соответственно в метрах и килограммах:
1 дин = 10-3 кг·10-2 м/с2;
в) выполним алгебраические действия с числами и наименованиями единиц:
1 дин = 10-5 кг·м/с2.
Но 1 кг·м/с2 есть ньютон, следовательно,
1 дин = 10-5 Н.
Однако нет необходимости производить запись для каждого пункта правил в отдельности. Рекомендуется следующая, более короткая запись:
1 дин = 1 г·см/с2 = 10-3 кг·10-2 м/с2 = 10-5 кг·м/с2 = 10-5 Н.
Пример 2. Выразить единицу работы СГС - эрг в джоулях:
1 эрг = 1 г·см2/с2 = 10-3 кг·(10-2 м)2/с2 = 10-3 кг·10-4 м2/с2 = 10-7 кг·м2/с2.
Следовательно, 1 эрг = 10-7 Дж
Эрг можно записать также через производные единицы той же системы СГС:
1 эрг = 1 дин·см.
И, если соотношение между диной и ньютоном известно, то выразив дину в ньютонах и сантиметр в метрах, получим
1 эРг = 10-5 Н·10-2 м = 10-7 Н·м, или 1 эрг = 10-7 Дж.
Это же соотношение можно найти, пользуясь также размерностью работы:
dim A = L2MT-2.
Согласно формуле (2.11) получим
1 Дж/1 эрг = (1 м/1 см)2·(1 кг/1 г)·(1 с/1 с)-2 = (100)2·(1000)·(1)-2 = 107,
откуда
1 эрг = 10-7 Дж.
Пример 3. Выразить единицу силы в системе МКГСС - килограмм-силу в ньютонах.
Известны опытные факты: а) тело массой 1 кг под действием силы 1 Н приобретает ускорение 1 м/с2, б) то же тело под действием силы тяжести, равной 1 кгс, получает при свободном падении ускорение, равное 9,81 м/с2. Запишем эти два положения:
сила 1 Н сообщает телу массой 1 кг ускорение 1 м/с2;
сила 1 кгс сообщает телу массой 1 кг ускорение 9,81 м/с2.
Таким образом, ускорение, сообщаемое телу силой 1 кгс, в 9,81 раза больше ускорения, сообщаемого тому же телу силой 1 Н. Следовательно, сила 1 кгс в 9,81 раза больше силы 1 Н, т.е.
1 кгс = 9,81 Н.
Пример 4. Выразить внесистемную единицу давления - техническую атмосферу (1 ат) в паскалях.
По определению,
1 ат = 1 кгс/см2.
Выразив в правой части равенства килограмм-силу в ньютонах и сантиметр в метрах, получим
1 ат = 9,81 Н/(10-2 м)2 = 9,81 Н/10-4 м2 = 9,81·104 Н/м2.
Следовательно,
1 ат = 9,81·104 Па.
Пример 5. Выразить внесистемную единицу мощности - лошадиную силу (л. с.) в ваттах.
По определению,
1 л. с. = 75 кгс·м/с.
Выразив в правой части равенства килограмм-силу в ньютонах, получим
1 л. с. = 75·9,81 Н·м/с = 736 Н·м/с = 736 Дж/с.
Следовательно,
1 л.с. = 736 Вт.
Пример 6. Выразить внесистемную единицу теплопроводности - 1 ккал/(м·ч·К) в ваттах на метр-кельвин. По определению,
1 кал = 4,19 Дж.
Следовательно,
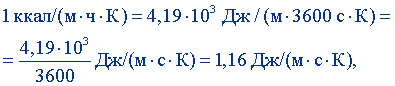
или окончательно
1 ккал/(м·ч·К) = 1,16 Вт/(м·К).
Пример 7. Выразить единицу электрической емкости СГС в фарадах.
Как известно,
1 ед. СГСC = 1 ед. СГСQ/ед. СГСφ.
Сделав в этом равенстве подстановку согласно соотношениям:
1 ед. СГСQ = 1/3·10-9 Кл, 1 ед. СГСφ = 300 В,
получим
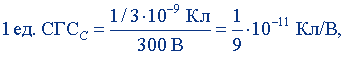
или
1 ед. СГСC = 1,11·10-12 Ф.
Пример 8. Выразить внесистемную единицу электрической энергии - киловатт-час (кВт-ч) в джоулях:
1 кВт·ч = 103 Вт·3600 с = 3,6·106 Вт·с,
или
1 кВт·ч = 3,6·106 Дж.
Приведем несколько примеров перевода числовых значений физических величин в Международную систему.
Пример 1. Выразить плотность железа в единицах Международной системы, если она, если она задана в единицах СГС:
ρ = 7,8 г/см3.
Выразим грамм в килограммах, кубический сантиметр в кубических метрах, т.е. произведем подстановку: 1 г = 10-3 кг, 1 см3 = 1·(0,01 м)3 = 10-6 м3, тогда получим
ρ = 7,8·10-3 кг/10-6 м3 = 7,8·103 кг/м3.
Пример 2. Выразить молярную газовую постоянную в единицах Международной системы, если она задана во внесистемных единицах:
R = 0,082 л·атм·К-1·моль-1.
Сделаем подстановку 1 л = 10-3 м3, 1 атм = 1,01·105 Па. После этого получим
R = 0,082·10-3 м3·1,01·105 Па·К-1·моль-1.
Произведя действия с числами, а также заметив, что 1 м3·Па = 1м3·Н/м2 = 1 Н·м = 1 Дж, найдем
R = 8,32 Дж·К-1·моль-1.
Пример 3. Выразить удельную теплоемкость воды в единицах Международной системы, если она задана во внесистемных единицах:
с = 1 кал/(г·К).
Сделав подстановку 1 кал = 4,19 Дж, 1 г =10-3 кг, получим удельную теплоемкость воды в СИ:
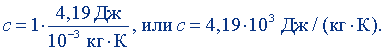
Пример 4. Выразить удельную теплоту сгорания нефти в единицах, кратных от единиц СИ.
Как известно, удельная теплота сгорания нефти
q = 11000 ккал/кг.
Выразив килокалорию в джоулях (1 ккал = 4,19·103 Дж), получим
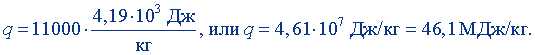
Пример 5. Выразить поверхностное натяжение воды в Международной системе, если оно задано в единицах СГС:
α = 72 дин/см.
Произведем подстановку 1 дин = 10-5 Н, 1 см = 10-2 м. Тогда получим
α = 72·10-5 Н/10-2 м = 7,2·10-2 Н/м, или α = 0,072 Н/м.
Числовое значение коэффициента при выражении его в единицах СИ получилось дробным и неудобным для пользования. Поэтому выразим поверхностное натяжение воды в дольных единицах, а именно в миллиньютонах на метр:
α = 72 мН/м.
Обратим внимание на то, что числовое значение в этом случае равно числовому значению при выражении поверхностного натяжения в динах на сантиметр.
Пример 6. Выразить модуль Юнга стали в единицах СИ, если он задан во внесистемных единицах:
E = 2·104 кгс/мм2.
Так как 1 кгс = 9,81 Н, 1 мм2 = 10-6 м2, то
E = 2·104·9,81 H/10-6 м2, или E ≈ 2·1011 Па.
Числовое значение модуля Юнга при выражении его в единицах СИ получилось очень большим. Следовательно, паскаль по своему размеру неудобен для выражения модуля Юнга стали. Эту величину надо выразить в единицах, кратных паскалю. Чтобы установить, какими именно кратными единицами удобнее при этом пользоваться, выразим модуль Юнга стали в различных кратных единицах:
E = 2·108 кПа, E = 2·105 МПа, E = 200 ГПа, E = 0,2 ТПа.
Из четырех числовых значений третье (200) наиболее удобно, поэтому модуль Юнга стали целесообразно выражать в гигапаскалях:
E = 200 ГПа.
Пример 7. Выразить предел прочности алюминия при растяжении в единицах СИ, если он задан во внесистемных единицах:
σпр = 9 кгс/мм2.
Выразив 1 кгс в ньютонах, 1 мм2 в квадратных метрах, получим
σпр = 9·9,81 Н/(10-3 м)2 = 8,83·107 Н/м2 = 8,83·107 Па.
Числовое значение получилось большим и потому неудобным. Выразим эту величину в различных кратных единицах:
σпр = 88,3 МПа, σпр = 0,883 ГПа.
Наиболее удобным числом является 88,3, поэтому предел прочности алюминия при растяжении целесообразно выражать в мегапаскалях:
σпр = 88,3 МПа.
Пример 8. Выразить удельное сопротивление железа в единицах Международной системы, если оно задано во внесистемных единицах:
ρ = 11·10-6 Ом·см.
Сделав в этом выражении подстановку 1 см = 10-2 м (Ом заменять не надо, так как в Международной системе сопротивление выражается в омах), получим
ρ = 11·10-6 Ом·10-2 м, или ρ = 1,1·10-7 Ом·м.
Пример 9. Выразить постоянную закона Стефана - Больцмана в единицах Международной системы, если она задана в единицах СГС:
σ = 5,67·10-5 эрг/(см2·с·К4).
В этом выражении сделаем подстановку 1 см = 10-2 м, 1 эрг = 10-7 Дж. После этого получим
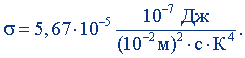
Выполнив действия с числовыми коэффициентами, найдем
σ = 5,67·10-8 Дж/(м2·с·К4).
⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨
МЕНЮ САЙТА / СОДЕРЖАНИЕ