Я создала и активно наполняю телеграм-канал "Перець". Здесь лучшие карикатуры из журнала, начиная с 1922 года.
Заходите, подписывайтесь: https://t.me/cartalana

ЧЕРТОВ А.Г. "ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН", 1977

МЕНЮ САЙТА / СОДЕРЖАНИЕ

Поверхностная плотность электрического заряда. Поверхностной плотностью электрического заряда σ называют величину, равную отношению заряда dQ, находящегося на элементе поверхности, к площади dS этой поверхности, т.е.

σ = dQ/dS.

Если электрический заряд равномерно распределен по поверхности площадью S, то

σ = Q/S. (9.3)

Положив Q = 1 Кл, S = 1 м², получим единицу поверхностной плотности электрического заряда:

[σ] = 1 Кл/1 м² = 1 Кл/м².

Кулон на квадратный метр равен поверхностной плотности электрического заряда, при которой заряд, равномерно распределенный по поверхности площадью 1 м², равен 1 Кл. Размерность поверхностной плотности заряда:

dim σ = L^-2TI.

Пространственная плотность электрического заряда (объемная плотность заряда). Пространственная плотность электрического заряда ρ есть величина, равная отношению заряда dQ, находящегося в элементе пространства, к объему dV этого элемента, т.е.

ρ = dQ/dV.

При равномерном распределении заряда

ρ = Q/V. (9.4)

Положив Q = 1 Кл, V = 1 м³, получим единицу пространственной плотности электрического заряда

[ρ] = 1 Кл/1 м³ = 1 Кл/м³.

Кулон на кубической метр равен пространственной (объемной) плотности электрического заряда, при которой заряд, равномерно распределенный в пространстве объемом 1 м³, равен 1 Кл. Размерность пространственной плотности заряда:

dim ρ = L^-3TI.

Диэлектрическая проницаемость (относительная диэлектрическая проницаемость). Диэлектрическая проницаемость ε_r среды показывает, во сколько раз сила взаимодействия F электрических зарядов в данной среде меньше, чем сила взаимодействия F₀ зарядов в вакууме, т.е.

ε_r = F₀/F. (9.5)

Из формулы (9.5) следует, что диэлектрическая проницаемость - величина безразмерная и, следовательно, выражается в безразмерных единицах.

Электрическая постоянная. Единицу электрической постоянной ε₀ установим, пользуясь законом Кулона:

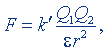* (9.6)

где F - сила взаимодействия точечных зарядов Q₁ и Q₂, находящихся на расстоянии r в среде с диэлектрической проницаемостью ε, kʹ - коэффициент пропорциональности.

* Здесь и далее в целях упрощения записи условимся в обозначении относительной диэлектрической проницаемости индекс "r" опускать.

Этот коэффициент пропорциональности нельзя положить равным безразмерной единице, так как единицы всех величин, входящих в закон Кулона, определены ранее. Единицу и размерность коэффициента kʹ можно было бы определить по формуле (9.6), а числовое его значение - опытным путем.

Однако поступают иначе. В целях придания формуле закона Кулона более симметричного вида коэффициент kʹ заменяют другим коэффициентом - электрической постоянной 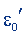, полагая

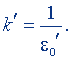(9.7)

После такой замены закон Кулона приобретает вид

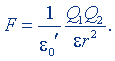(9.8)

Так записывался закон Кулона в классической нерационализованной системе МКСА.

В Международной системе единиц закон Кулона записывается в рационализованной форме, т.е. с множителем 4π в знаменателе коэффициента пропорциональности:

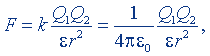(9.8а)

где

k = 1/4πε₀. (9.7a)

Для определения единицы электрической постоянной выразим ее из формул (9.8) и (9.8а) соответственно

εʹ₀ε = Q₁Q₂/εFr², (9.9)

ε₀ = Q₁Q₂/4πεFr². (9.9а)

Отсюда получим

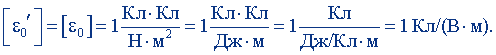
Эта единица называется кулон на вольт-метр.

Однако такое наименование не является широко употребительным. В ГОСТ 8033-56 единице электрической постоянной присвоено наименование фарада на метр (Ф/м).

Электрическая постоянная относится к числу, физических постоянных (фундаментальных физических констант) и имеет значение

ε₀ = 8,85418782·10^-12 Ф/м,

или приближенно

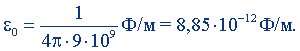
Размерность ε₀ получим по формулам (9.9) и (9.9а):

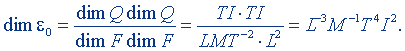
Значение коэффициента пропорциональности k найдем, подставив в формулу (9.7а) значение ε₀:

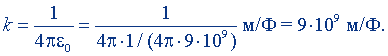
Абсолютная диэлектрическая проницаемость. Абсолютная диэлектрическая проницаемость ε_а диэлектрика - величина, равная произведению его диэлектрической проницаемости ε и электрической постоянной ε₀, т.е.

ε_а = εε₀. (9.10)

Один из множителей этой величины - относительная диэлектрическая проницаемость ε зависит только от свойств вещества и не зависит от системы единиц, другой множитель - электрическая постоянная ε₀ зависит только от выбора системы единиц.

Так как относительная диэлектрическая проницаемость - величина безразмерная, то абсолютная диэлектрическая проницаемость выражается в тех же единицах, что и электрическая постоянная, т.е. в кулонах на вольтметр или фарадах на метр и имеет размерность:

dim ε_а = L^-3M^-1T⁴I².

Напряженность электрического поля. Напряженностью Е электрического поля в точке называют величину, равную отношению силы F, с которой поле действует на положительный заряд, помещенный в данную точку поля, к этому заряду Q, т.е.

E = F/Q. (9.11)

Подставив F = 1 Н, Q = 1 Кл, получим единицу напряженности электрического поля:

[E] = 1 Н/1 Кл = 1 Н/Кл.

Ньютон на кулон равен напряженности электрического поля, в котором на точечный заряд 1 Кл действует сила 1 Н. На практике эта единица напряженности носит название вольт на метр и определяется на основе формулы, устанавливающей связь между напряженностью поля и разностью потенциалов. Размерность напряженности:

dim E = LMT^-3I^-1.

Поток напряженности электрического поля (поток вектора напряженности). Потоком dN напряженности электрического поля через элемент поверхности называют величину, равную произведению проекции Е_n напряженности поля на вектор нормали n к элементу поверхности на площадь dS этого элемента:

dN = E_ndS.

Поток через всю поверхность

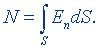
Если в однородном поле перпендикулярно силовым линиям расположена плоская поверхность площадью S, то поток напряженности через нее

N = ES. (9.12)

Подставив E = 1 В/м, S = 1 м², получим единицу потока напряженности:

[N] = 1 В/м · 1 м² = 1 В·м.

Вольт-метр равен потоку напряженности через плоскую поверхность площадью 1 м² установленную перпендикулярно силовым линиям однородного поля напряженностью 1 В/м. Размерность потока напряженности:

dim N = dim E · dim S = LMT^-3I^-1 · L² = L³MT^-3I^-1.

Электрический потенциал (потенциал электрического поля). Электрическим потенциалом φ в точке называют величину, равную отношению потенциальной энергии, которой обладает положительный заряд, помещенный в данную точку поля, к этому заряду. Потенциальная энергия заряда Q в данной точке поля равна работе А, которую совершают силы электрического поля при перемещении заряда из данной точки в бесконечность. Поэтому потенциал может быть определен как величина, численно равная работе, совершаемой полем при удалении единичного положительного заряда из данной точки в бесконечность, т.е.

φ = A/Q. (9.13)

Подставив А = 1 Дж, Q = 1 Кл, получим

[φ] = 1 Дж/1 Кл = 1 Дж/Кл.

Эта единица называется вольт (В). Вольт равен потенциалу точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж. В вольтах выражаются также напряжение и электродвижущая сила. Размерность потенциала:

dim φ = L²MT^-3I^-1.

Градиент потенциала. Градиент потенциала (grad φ) - вектор, направленный по нормали n к эквипотенциальной поверхности в сторону возрастания потенциала и равный dφ/dn, т.е.

grad φ = dφ/dn·i,

где i - единичный вектор нормали. В случае однородного поля будет справедливо равенство

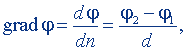(9.14)

где d - расстояние между эквипотенциальными поверхностями, (φ₂ - φ₁) - разность потенциалов этих поверхностей.

Положив в (9.14) φ₂ - φ₁, = 1 В, d = 1 м, найдем

[grad φ] = 1 В/1 м = 1 В/м.

Между градиентом потенциала и напряженностью электрического поля существует соотношение

Е = -grad φ, (9.15)

т.е. напряженность поля в некоторой точке равна градиенту потенциала в этой же точке, взятому с обратным знаком.

Для однородного поля связь напряженности и потенциала выразится формулой

E = (φ₁ - φ₂)/d. (9.16)

Из (9.15) и (9.16) следует, что напряженность поля может выражаться в тех же единицах, что и градиент потенциала, т.е. в вольтах на метр. Размерность градиента потенциала:

dim grad φ = LMT^-3T^-1.

Электрический момент диполя (дипольный момент). Электрический диполь - система двух равных и противоположных по знаку электрических зарядов. Электрический момент р диполя есть вектор, направленный от отрицательного заряда к положительному и равный произведению заряда Q на плечо l диполя, т. с.

p = Ql. (9.17)

Единицу электрического момента диполя найдем, если в (9.17) положим Q = 1 Кл, l = 1 м:

[р] = 1 Кл · 1 м = 1 Кл·м.

Кулон-метр равен электрическому моменту диполя, заряды которого равные каждый 1 Кл, расположены на расстоянии 1 м один от другого. Размерность электрического момента диполя:

dim p = LTI.

Поляризованность (вектор поляризации, интенсивность поляризации). Диэлектрик, помещенный в электрическое поле, поляризуется. При этом любой элемент диэлектрика приобретает электрический момент. Степень поляризации диэлектрика характеризуется поляризованностью. Поляризованность Р - величина, равная отношению электрического момента dp элемента диэлектрика к объему dV этого элемента:

P = dp/dV.

В случае равномерной поляризации

P = p/V, (9.18)

где р - электрический момент диэлектрика объемом V.

Положив в (9.18) р = 1 Кл·м, V = 1 м³, получим единицу поляризованности:

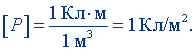
Кулон на квадратный метр равен поляризованности диэлектрика, при которой диэлектрик объемом 1 м³ имеет электрический момент 1 Кл·м. Размерность поляризованности:

dim P = L^-2TI.

Она одинакова с размерностью поверхностной плотности электрического заряда.

Абсолютная диэлектрическая восприимчивость. Поляризованность диэлектрика пропорциональна напряженности Е поля внутри этого диэлектрика, т.е.

P = k_aE, (9.19)

где k_a - коэффициент пропорциональности, называемый абсолютной диэлектрической восприимчивостью. Из (9.19) получим

k_a = Р/Е. (9.20)

Отсюда следует, что абсолютная диэлектрическая восприимчивость численно равна поляризованности диэлектрика при напряженности поля, равной единице.

Единицу абсолютной диэлектрической восприимчивости найдем, положив в (9.20) Р = 1 Кл/м², E = 1 В/м:

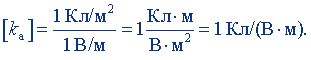
Эту единицу называют кулон на вольт-метр, или фарада на метр (Ф/м). Фарада на метр равна абсолютной диэлектрической восприимчивости диэлектрика, поляризованность которого 1 Кл/м² при напряженности поля 1 В/м.

Абсолютная диэлектрическая восприимчивость выражается в тех же единицах, в которых выражаются электрическая постоянная ε₀ и абсолютная диэлектрическая проницаемость ε_а. Размерность абсолютной диэлектрической восприимчивости:

dim k_a = L^-3M^-1T⁴I².

⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨

МЕНЮ САЙТА / СОДЕРЖАНИЕ