
Я создала и активно наполняю телеграм-канал "Перець". Здесь лучшие карикатуры из журнала, начиная с 1922 года.
Заходите, подписывайтесь: https://t.me/cartalana

ЧЕРТОВ А.Г. "ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН", 1977
Чтобы найти размерность скорости, подставим в формулу (2.1) вместо длины пути s и времени t их размерности L и Т:
размерность скорости = L/T = LT-1.
Условимся обозначать размерность величины символом dim *. Тогда размерность скорости запишется в виде
dim v = LT-1.
* Сокращенное от английского слова "dimension", что означает в переводе на русским язык "размер", "размерность".
Определяющими уравнениями площади и объема являются формулы:
s = a2, V = b3 (2.3)
где а - длина стороны квадрата, b - длина ребра куба. Подставив вместо а и b размерность L, найдем размерности площади и объема:
dim S = L2, dim V = L3.
Найти же размерность силы F по ее определяющему уравнению (2.2) было бы затруднительно, так как нам неизвестна размерность ускорения а. Прежде чем определять размерность силы, надо найти размерность ускорения, используя формулу ускорения равнопеременного движения:
а = Δv/Δt, (2.4)
где Δv - изменение скорости тела за время Δt.
Подставив сюда уже известные нам размерности скорости и времени, получим
dim a = LT-1/T = LT-2.
Теперь по формуле (2.2) найдем размерность силы:
dim F = M·LT-2 = LMT-2.
Точно так же для получения размерности мощности N по ее определяющему уравнению N = A/t, где А - работа, совершенная за время t, необходимо предварительно найти размерность работы.
Из приведенных примеров следует, что не безразлично, в какой последовательности надо расположить определяющие уравнения при построении данной системы величин, т.е. при установлении размерностей производных величии.
Последовательность расположения производных величин при построении системы должна удовлетворять следующим условиям: 1) первой должна быть величина, которая выражается только через основные величины; 2) каждая последующая должна быть величиной, которая выражается только через основные и такие производные, которые ей предшествуют.
В качестве примера приведем в таблице последовательность величин, которая удовлетворяет таким условиям:
| № п/п | Физическая величина | Определяющее уравнение | Размерность величины |
| 1 | Площадь | S = a2 | L2 |
| 2 | Объем | V = b3 | L3 |
| 3 | Скорость | v = s/t | LT-1 |
| 4 | Момент инерции | J = mr2 | L2M |
| 5 | Плотность | ρ = m/V | L-3M |
| 6 | Удельный объем | v = V/m | L3M-1 |
| 7 | Ускорение | а = Δv/Δt | LT-2 |
| 8 | Импульс тела | p = mv | LMT-1 |
| 9 | Момент импульса | L = mvr | L2MT-1 |
| 10 | Сила | F = ma | LMT-2 |
| 11 | Момент силы | M = Fr | L2MT-2 |
| 12 | Давление | p = F/S | L-1MT-2 |
| 13 | Работа, энергия | A = Fs | L2MT-2 |
| 14 | Мощность | N = A/t | L2MT-3 |
Последовательность величин, приведенная в таблице, не является единственной, удовлетворяющей указанному выше условию. Отдельные величины в таблице могут быть переставлены. Например, плотность (строка 5) и момент инерции (строка 4) или момент силы (строка 11) и давление (строка 12) можно поменять местами, так как размерности этих величин определяются независимо друг от друга.
Но плотность в этой последовательности нельзя поставить раньше объема (строка 2), так как плотность выражается через объем и для определения ее размерности необходимо знать размерность объема. Момент силы, давление и работа (строка 13) не могут быть поставлены раньше силы, так как для определения их размерности надо знать размерность силы.
Из приведенной таблицы следует, что размерность любой физической величины х в системе LMT в общем виде может быть выражена равенством
dim x = LαMβTγ, (2.5)
где α, β, γ - целые числа.
В системе величин механики LFT размерность величины выразится в общем виде формулой
dim x = LαFβTγ. (2.6)
Приведем в общем виде формулы размерности соответственно в системах величин: LMTI, в электростатической и электромагнитной LMT, в LMTΘ и в любой системе с числом основных величин больше трех:
dim x = LαMβTγIδ, (2.7)
dim х = LαМβТγ, (2.8)
dim x = LαMβTγΘε, (2.9)
dim x = LαMβTγ ... (2.10)
Из формул (2.5)-(2.10) следует, что размерность величины представляет собой произведение размерностей основных величин, возведенных в соответствующие степени.
Показатель степени (α, β, γ ...), в которую возведена размерность основной величины, входящая в размерность производной величины, называется показателем размерности физической величины. Как правило, показатели размерности являются целыми числами. Исключение составляют показатели в электростатической и электромагнитной системах LMT, в которых они могут быть и дробными.
Некоторые показатели размерности могут оказаться равными нулю. Так, записав размерности скорости и момента инерции в системе LMT в виде
dim v = LT-1 = LM0T-1,
dim J = L2M = L2MT0,
находим, что у скорости равен нулю показатель размерности β, у момента инерции - показатель размерности γ.
Может оказаться, что все показатели размерности некоторой величины равны нулю. Такая величина называется безразмерной. Безразмерными величинами являются, например, относительная деформация, относительная диэлектрическая проницаемость.
Величина называется размерной, если в ее размерности хотя бы одна из основных величин возведена в степень, не равную нулю.
Конечно, размерности одной и той же величины в различных системах могут оказаться разными. В частности, величина безразмерная в одной системе может оказаться размерной в другой системе. Например, абсолютная диэлектрическая проницаемость в электростатической системе LMT является безразмерной величиной, в электромагнитной системе LMT ее размерность равна L-2T2, а в системе величин LMTI - L-3M-1T4I2.
Эти примеры показывают, что размерность не есть нечто абсолютное. Понятие размерности есть понятие относительное, поэтому об определенных размерностях физических величин можно говорить, только оставаясь в рамках одной системы величии.
Однако это не мешает использованию размерностей как эффективного средства исследования ряда вопросов метрического характера. Остановимся кратко на некоторых из них.
1. Размерность позволяет определить, как изменяется размер производной величины при изменении размеров основных величин. Если размерность величины х равна LαMβTγ и длина изменяется от l до lʹ, масса - от m до mʹ и время - от t до tʹ, то новый размер величины будет больше прежнего в (lʹ/l)α (mʹ/m)β (tʹ/t)γ раз, т.е.
хʹ/х = (lʹ/l)α(mʹ/m)β (tʹ/t)γ. (2.11)
Пример. Определим, как изменится момент инерции системы с увеличением линейных размеров в 2 раза и массы в 3 раза.
Равномерность момента инерции
dim J = L2M.
Пользуясь формулой (2.11), получим
Jʹ/J = (lʹ/l)2(mʹ/m) = 22·3 = 12.
Следовательно, момент инерции увеличится в 12 раз.
2. Пользуясь размерностями физических величин, можно определить, как изменится размер производной единицы с изменением размеров основных единиц, через которые она выражается, а также установить соотношение единиц в разных системах.
3. Размерности физических величин позволяют обнаружить ошибки при решении физических задач.
Получив в результате решения расчетную формулу, следует проверить, совпадают ли размерности левой и правой частей формулы. Несовпадение этих размерностей свидетельствует о том, что в ходе решения задачи была допущена ошибка. Конечно, совпадение размерностей еще не означает, что задача решена правильно.
Рассмотрение других практических приложений размерностей выходит за рамки настоящего пособия.
§ 3. ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН. РАЗМЕР ЕДИНИЦ
Измерение физических величин возможно лишь в том случае, если для каждой из них выбраны соответствующие единицы.
Единица физической величины - это физическая величина, которой по определению присвоено числовое значение, равное 1.
Так как в практической деятельности человека приходится измерять величины разных размеров, то для одной и той же величины может быть несколько единиц, отличающихся друг от друга размером. Например, единицы длины - метр, дюйм, ангстрем (Å), астрономическая единица длины (а. е. д.) имеют разные размеры: 1 дюйм = 25,4 · 10-2 м, 1 Å = 10-10 м, 1 а. е. д. = 1,49 ·1011 м.
Покажем, что числовые значения данной физической величины обратно пропорциональны размерам единиц, в которых эта величина выражена. Подставив в формулу
(1.1) разные по размеру единицы [X]1 и [Х]2, получим:
X = {X}1[X]1, X = {X}2[X]2.
Так как значение конкретной величины не зависит от того, в каких единицах она выражена (например, 1,2 м = 120 см = 1200 мм), то из последних двух равенств следует
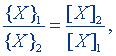 (3.1)
(3.1)
т.е. числовые значения величины обратно пропорциональны размерам единиц.
Из соотношения (3.1) найдем
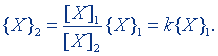 (3.2)
(3.2)
Формула (3.2) позволяет определить числовое значение величины, выраженной в некоторой единице [Х]2, если известно числовое значение этой величины, выраженной в единице [X]1. Числовой множитель k, равный отношению единиц, называется коэффициентом пересчета.
⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨
МЕНЮ САЙТА / СОДЕРЖАНИЕ