Ł Старые понятные учебники советских времен по физике, математике. Акупунктура, похудение

КАБАРДИН О.Ф. "ФИЗИКА (справочные материалы)", 1991

Невесомость. Если тело вместе с опорой свободно падает, то , и из формулы (10.7) следует, что .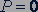

Исчезновение веса при движении опоры с ускорением свободного падения называется невесомостью.

Состояние невесомости наблюдается в самолете или космическом корабле при движении с ускорением свободного падения независимо от направления и значения модуля скорости их движения. За пределами земной атмосферы при выключении реактивных двигателей на космический корабль действует только сила всемирного тяготения. Под действием этой силы космический корабль и все тела, находящиеся в нем, движутся с одинаковым ускорением; поэтому в корабле наблюдается явление невесомости.

Перегрузка. При ускоренном движении тела и опоры с ускорением, направленным вертикально вверх (рис. 30), вес тела оказывается больше действующей на него силы тяжести.

Рис. 30

В этом случае проекции и положительны, а проекция 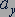отрицательна. Поэтому для модуля веса тела: получаем выражение

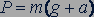. (10.8)

Увеличение веса тела, вызванное ускоренным движением опоры или подвеса, называют перегрузкой. Действие перегрузки испытывают на себе космонавты как при взлете космической ракеты, так и на участке торможения космического корабля при входе в плотные слои атмосферы. Испытывают перегрузки и летчики при выполнении фигур высшего пилотажа, и водители автомобилей при движении с большими ускорениями.>

11. ДВИЖЕНИЕ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ

Рассмотрим вопрос о движении тел под действием силы тяжести. Если модуль перемещения тела много меньше расстояния до центра Земли, то можно считать силу всемирного тяготения во время движения постоянной, а движение тела равноускоренным. Самый простой случай движения тел под действием силы тяжести - свободное падение с начальной скоростью, равной нулю. В этом случае тело движется прямолинейно с ускорением свободного падения по направлению к центру Земли. Если начальная скорость тела отлична от нуля и вектор начальной скорости направлен не по вертикали, то тело под действием силы тяжести движется с ускорением свободного падения по криволинейной траектории. Форму такой траектории наглядно иллюстрирует струя воды, вытекающая под некоторым углом к горизонту (рис. 31).

Рис. 31

При бросании тела с некоторой высоты параллельно земной поверхности дальность полета будет тем большей, чем больше начальная скорость.

При больших значениях начальной скорости необходимо учитывать шарообразность Земли и изменение направления вектора силы тяжести в разных точках траектории.

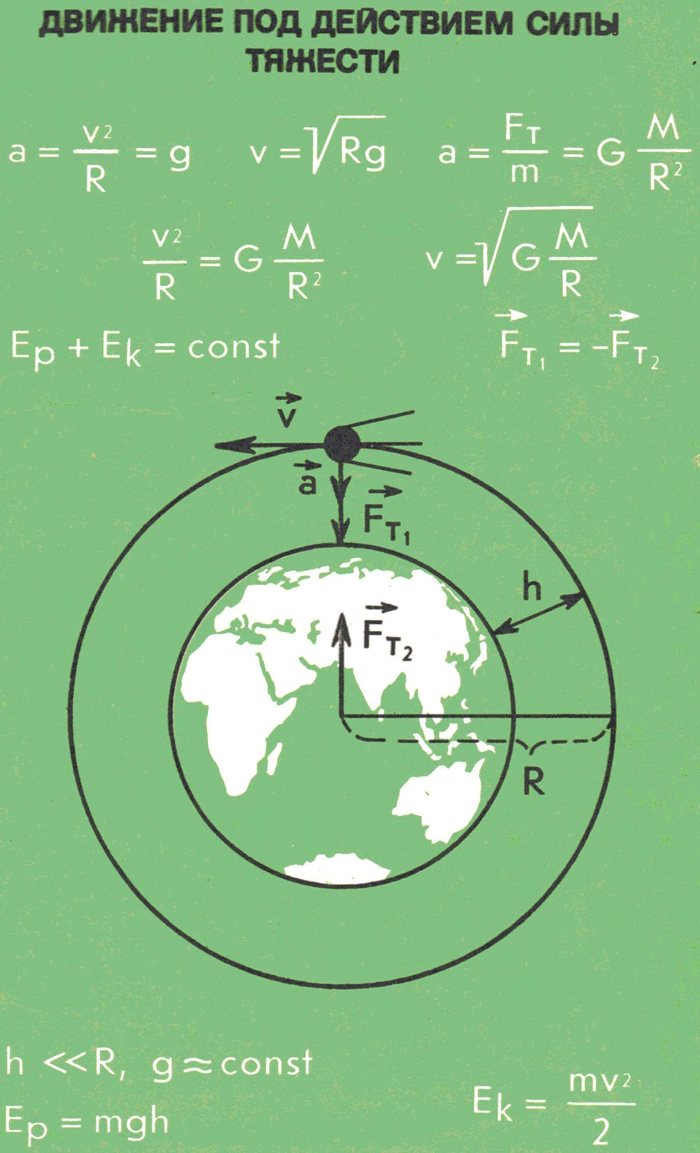
Первая космическая скорость. При некотором значении начальной скорости тело, брошенное по касательной к поверхности Земли, под действием силы тяжести при отсутствии атмосферы может двигаться вокруг Земли по окружности, не падая на Землю и не удаляясь от нее.

Скорость, с которой происходит движение тела по круговой орбите под действием силы всемирного тяготения, называется первой космической скоростью.

Определим первую космическую скорость для Земли (см. рисунок). Если тело под действием силы тяжести движется вокруг Земли равномерно по окружности радиусом 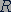, то ускорение свободного падения является его центростремительным ускорением:

. (11.1)

Отсюда первая космическая скорость равна

. (11.2)

Подставив в выражение (11.2) значение радиуса Земли и ускорения свободного падения у ее поверхности, получим, что первая космическая скорость для Земли . Эта скорость примерно в 8 раз больше скорости пули.

Первая космическая скорость для любого небесного тела также определяется выражением (11.2). Ускорение свободного падения на расстоянии 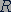от центра небесного тела можно найти, воспользовавшись вторым законом Ньютона и законом всемирного тяготения:

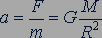. (11.3)

Из выражений (11.2) и (11.3) получаем, что первая космическая скорость на расстоянии 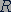от центра небесного тела массой 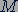равна

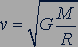. (11.4)

Рис. 32

Для запуска на околоземную орбиту искусственный спутник Земли или космический корабль необходимо сначала вывести за пределы атмосферы. Поэтому космические корабли стартуют вертикально. На высоте 200-300 км от поверхности Земли атмосфера очень разрежена и почти не влияет на движение космических кораблей. На такой высоте ракета делает поворот и сообщает аппарату, запускаемому на орбиту искусственного спутника, первую космическую скорость в направлении, перпендикулярном вертикали (рис. 32).

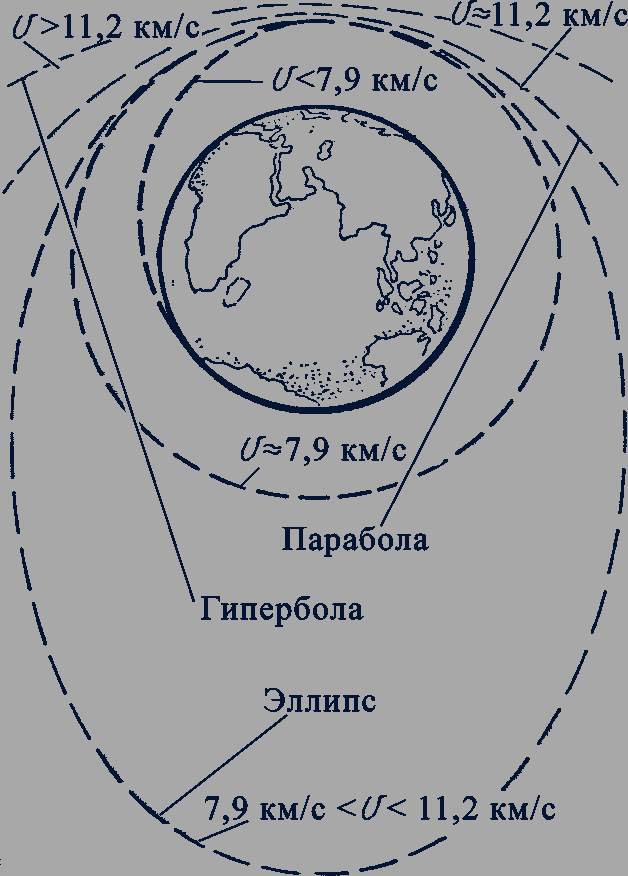
Рис. 33

Если космическому аппарату сообщается скорость меньше первой космической, то он движется по траектории, которая пересекается с поверхностью земного шара, т.е. аппарат падает на Землю. При начальной скорости больше 7,9 км/с, но меньше 11,2 км/с космический аппарат движется вокруг Земли по криволинейной траектории - эллипсу. Чем больше начальная скорость, тем все более вытянут эллипс.

При достижении некоторого значения скорости, называемого второй космической скоростью, эллипс превращается в параболу и космический корабль уходит от Земли безвозвратно. У поверхности Земли вторая космическая скорость равна 11,2 км/с. При скорости более второй космической тело движется по гиперболической траектории (рис. 33).

12. СИЛА УПРУГОСТИ

Вблизи поверхности Земли на любое тело действует сила тяжести, однако большинство тел вокруг нас не падают с ускорением, а находятся в покое. Неподвижны книга, лежащая на столе, и стол, стоящий на полу.

Книга на столе неподвижна, - значит, кроме силы тяжести, на нее действуют другие силы и равнодействующая всех сил равна нулю.

Какие же это силы и как они возникают?

Выполним следующий опыт. Положим стальную линейку на лапки штативов таким образом, чтобы линейка была расположена горизонтально. Против середины стальной линейки установим демонстрационную линейку и заметим по ее шкале начальное положение середины стальной линейки.

Затем подвесим к середине стальной линейки небольшую гирю. Мы увидим, что стальная линейка изогнется. Неподвижность гири показывает, что сила тяжести, действующая на нее со стороны Земли, уравновешена равной по модулю и противоположно направленной силой, возникающей при деформации линейки (рис. 34).

Сила, возникающая в результате деформации тела и направленная в сторону, противоположную перемещениям частиц тела при деформации, называется силой упругости.

Опыты по растяжению и сжатию твердых стержней показали, что при малых по сравнению с размерами тел деформациях модуль силы упругости прямо пропорционален модулю вектора перемещения свободного конца стержня. Направление вектора силы упругости противоположно направлению вектора перемещения при деформации (рис. 35). Поэтому для проекции силы упругости на ось 𝑂𝑋, направленную по вектору перемещения, выполняется равенство

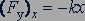, (12.1)

где - удлинение стержня.

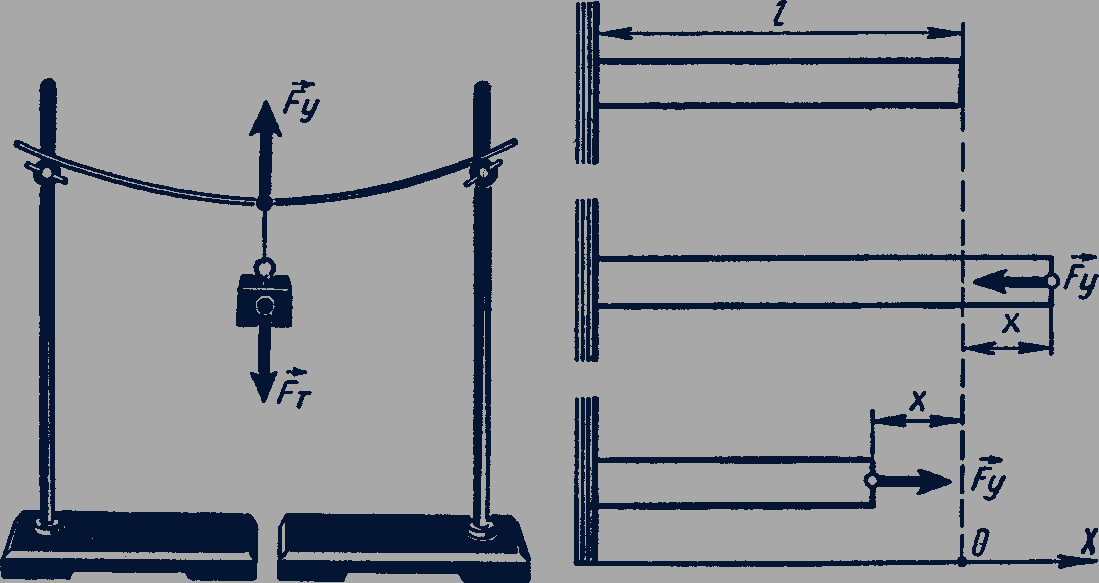
Рис. 34-35

Связь между проекцией силы упругости и удлинением тела была установлена экспериментально английским ученым Робертом Гуком (1635-1703) и поэтому называется законом Гука.

Сила упругости, возникающая при деформации тела, пропорциональна удлинению тела и направлена в сторону, противоположную направлению перемещений частиц тела при деформации.

Коэффициент пропорциональности 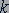в законе Гука называется жесткостью тела. Жесткость тела зависит от формы и размеров тела и от материала, из которого оно изготовлено. Жесткость в СИ выражается в ньютонах на метр (Н/м).

Выясним природу сил упругости. В состав атомов и молекул входят частицы, обладающие электрическими зарядами. Атомы в твердом теле расположены таким образом, что силы отталкивания одноименных электрических зарядов и притяжения разноименных зарядов уравновешивают друг друга. При изменениях взаимных положений атомов или молекул в твердом теле в результате его деформации электрические силы стремятся возвратить атомы в первоначальное положение. Так при деформации возникает сила упругости.

Силы взаимодействия электрических зарядов называются электромагнитными силами. Так как силы упругости обусловлены взаимодействиями зарядов, по своей природе они являются электромагнитными силами.

13. СИЛЫ ТРЕНИЯ

Силы трения покоя. Прикрепим к бруску крючок динамометра и попытаемся привести брусок в движение. Растяжение пружины динамометра показывает, что на брусок действует сила упругости, но тем не менее брусок остается неподвижным. Это значит, что при действии на брусок силы упругости в направлении, параллельном поверхности соприкосновения бруска со столом, возникает равная ей по модулю сила противоположного направления. Сила, возникающая на границе соприкосновения тел при отсутствии относительного движения тел, называется силой трения покоя.

Сила трения покоя 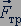равна по модулю внешней силе 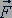, направленной по касательной к поверхности соприкосновения тел, и противоположна ей по направлению (рис. 36): .

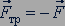Рис. 36

Сила трения скольжения. Прикрепим динамометр к бруску и заставим брусок двигаться равномерно по горизонтальной поверхности стола. Во время равномерного движения бруска динамометр показывает, что на брусок со стороны пружины действует постоянная сила упругости . При равномерном движении бруска равнодействующая всех сил, приложенных к нему, равна нулю. Следовательно, кроме силы упругости, во время равномерного движения на брусок действует сила, равная по модулю силе упругости, но направленная в противоположную сторону. Эта сила называется силой трения скольжения .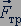

Вектор силы трения скольжения 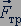всегда направлен противоположно вектору скорости v движения тела относительно соприкасающегося с ним тела. Поэтому действие силы трения скольжения всегда приводит к уменьшению модуля относительной скорости тел.

Природа силы трения. Силы трения возникают благодаря существованию сил взаимодействия между молекулами и атомами соприкасающихся тел. Последние обусловлены взаимодействием электрических зарядов, которыми обладают частицы, входящие в состав атомов.

Коэффициент трения. Исследуем, от чего зависит сила трения. Для этого воспользуемся гладкой деревянной доской, деревянным бруском и динамометром (рис. 37). Сначала проверим, зависит ли сила трения от площади поверхности соприкосновения тел. Положим брусок на горизонтально расположенную доску гранью с самой большой площадью поверхности. Прикрепив к бруску динамометр, будем плавно увеличивать силу, направленную вдоль поверхности доски, и заметим максимальное значение силы трения покоя. Затем поставим тот же брусок на другую грань с меньшей площадью поверхности и вновь измерим максимальное значение силы трения покоя. Опыт показывает, что максимальное значение силы трения покоя не зависит от площади поверхности соприкосновения тел.

Повторив такие же измерения при равномерном движении бруска по поверхности доски, убеждаемся, что сила трения скольжения также не зависит от площади поверхности соприкосновения тел.

Поставим на первый брусок второй такой же. Этим мы увеличим силу, перпендикулярную поверхности соприкосновения тела и стола (ее называют силой давления 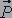). Если теперь мы вновь измерим максимальную силу трения покоя (рис. 38), то увидим, что она увеличилась в два раза. Поставив на два бруска третий, обнаруживаем, что максимальная сила трения покоя увеличилась в три раза.

Рис. 37-38

На основании таких опытов можно сделать вывод, что максимальное значение модуля силы трения покоя прямо пропорционально силе давления.

Взаимодействие тела и опоры вызывает деформацию и тела, и опоры.

Рис. 39

Силу упругости 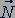, возникающую в результате деформации опоры и действующую на тело, называют силой реакции опоры (рис. 39). По третьему закону Ньютона сила давления и сила реакции опоры равны по модулю и противоположны по направлению:

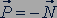Поэтому предыдущий вывод можно сформулировать так: модуль максимальной силы трения покоя пропорционален силе реакции опоры:

Греческой буквой обозначен коэффициент пропорциональности, называемый коэффициентом трения.

Опыт показывает, что модуль силы трения скольжения , как и модуль максимальной силы трения покоя, пропорционален модулю силы реакции опоры:

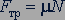Максимальное значение силы трения покоя примерно равно силе трения скольжения, приближенно равны также коэффициенты трения покоя и скольжения.

Силы трения возникают и при качении тела. При одинаковой нагрузке сила трения качения значительно меньше силы трения скольжения. Поэтому для уменьшения сил трения в технике применяются колеса, шариковые и роликовые подшипники.

14. УСЛОВИЯ РАВНОВЕСИЯ ТЕЛ

Статика. Основным признаком взаимодействия тел в динамике является возникновение ускорений. Однако часто бывает нужно знать, при каких условиях тело, на которое действует несколько различных сил, не движется с ускорением. Подвесим шар на нити. На шар действует сила тяжести, но не вызывает ускоренного движения к Земле. Этому препятствует действие равной по модулю и направленной в противоположную сторону силы упругости. Сила тяжести и сила упругости уравновешивают друг друга, их равнодействующая равна нулю, поэтому равно нулю и ускорение шара (рис. 40).

Точку, через которую проходит равнодействующая сил тяжести при любом расположении тела, называют центром тяжести (рис. 41).

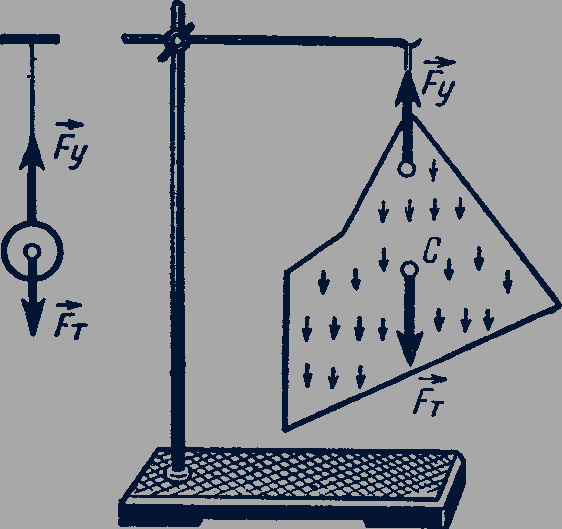
Рис. 40-41

Раздел механики, изучающий условия равновесия сил, называется статикой.

Равновесие невращающихся тел. Равномерное прямолинейное поступательное движение тела или его покой возможны только при равенстве нулю геометрической суммы всех сил, приложенных к телу.

Невращающееся тело находится в равновесии, если геометрическая сумма сил, приложенных к телу, равна нулю.

Равновесие тел, имеющих ось вращения. В повседневной жизни и технике часто встречаются тела, которые не могут двигаться поступательно, но могут вращаться вокруг оси. Примерами таких тел могут служить двери и окна, колеса автомобиля, качели и т.д. Если вектор силы 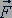лежит на прямой, пересекающей ось вращения, то эта сила уравновешивается силой упругости со стороны оси вращения (рис. 42).

Если же прямая, на которой лежит вектор силы 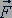, не пересекает ось вращения, то эта сила не может быть уравновешена силой упругости со стороны оси вращения, и тело поворачивается вокруг оси (рис. 43).

Вращение тела вокруг оси под действием одной силы 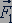может быть остановлено действием второй силы 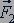. Опыт показывает, что если две силы 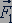и 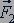по отдельности вызывают вращение тела в противоположных направлениях, то при их одновременном действии тело находится в равновесии, если выполняется условие:

где 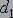и - кратчайшие расстояния от прямых, на которых лежат векторы сил 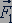и 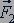(линии действия сил), до оси вращения (рис. 44). Расстояние 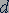называется плечом силы, а произведение модуля силы 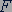на плечо 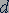называется моментом силы :

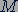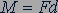. (14.1)

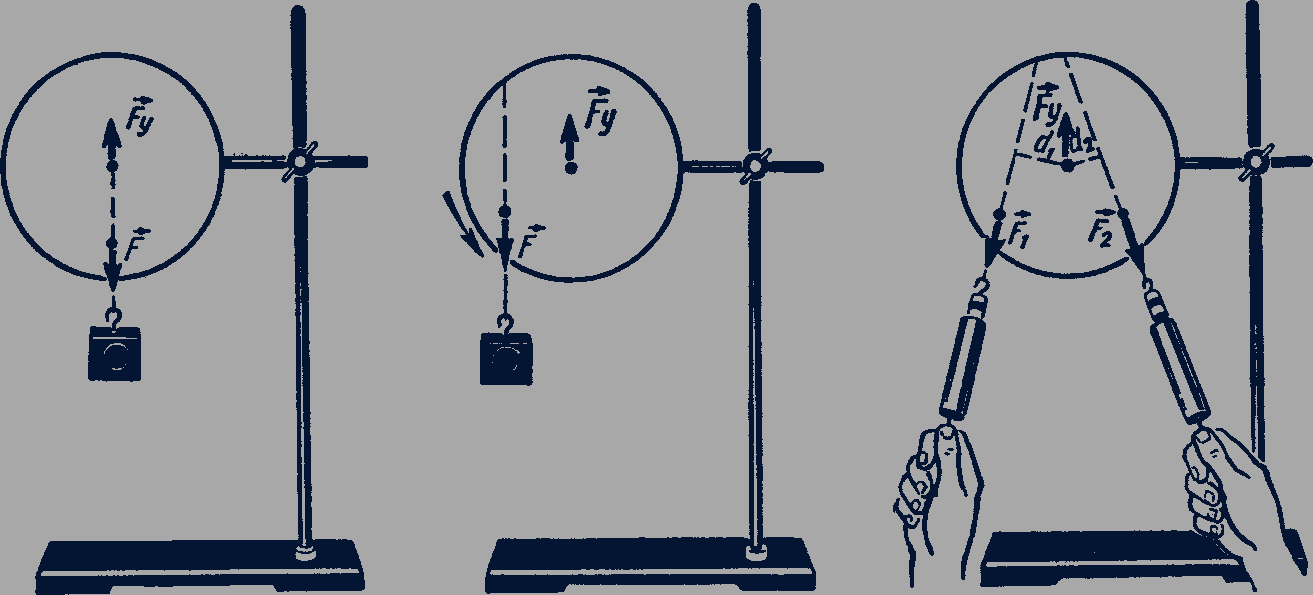
Рис. 42-43-44

Если моментам сил, вызывающим вращение тела вокруг оси по часовой стрелке, приписать положительный знак, а моментам сил, вызывающим вращение против часовой стрелки, - отрицательный знак, то условие равновесия тела, имеющего ось вращения, можно сформулировать в виде правила моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:

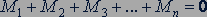. (14.2)

За единицу вращающего момента в СИ принимается момент силы в 1 Н, линия действия которой находится на расстоянии 1 м от оси вращения. Эту единицу называют ньютон-метром (Н·м).

Общее условие равновесия тела. Объединяя два вывода, можно сформулировать общее условие равновесия тела: тело находится в равновесии, если равны нулю геометрическая сумма векторов всех приложенных к нему сил и алгебраическая сумма моментов этих сил относительно оси вращения.

При выполнении общего условия равновесия тело необязательно находится в покое. Согласно второму закону Ньютона при равенстве нулю равнодействующей всех сил ускорение тела равно нулю и оно может находиться в покое или двигаться равномерно и прямолинейно.

Равенство нулю алгебраической суммы моментов сил не означает также, что при этом тело обязательно находится в покое. На протяжении нескольких миллиардов лет с постоянным периодом продолжается вращение Земли вокруг оси именно потому, что алгебраическая сумма моментов сил, действующих на Землю со стороны других тел, очень мала. По той же причине продолжает вращение с постоянной частотой раскрученное велосипедное колесо, и только внешние силы останавливают это вращение.

Виды равновесия. В практике большую роль играет не только выполнение условия равновесия тел, но и качественная характеристика равновесия, называемая устойчивостью. Различают три вида равновесия тел: устойчивое, неустойчивое и безразличное. Равновесие называется устойчивым, если после небольших внешних воздействий тело возвращается в исходное состояние равновесия. Это происходит, если при небольшом смещении тела в любом направлении от первоначального положения равнодействующая сил, действующих на тело, становится отличной от нуля и направлена к положению равновесия. В устойчивом равновесии находится, например, шар на дне углубления (рис. 45).

Равновесие называется неустойчивым, если при небольшом смещении тела из положения равновесия равнодействующая приложенных к нему сил отлична от нуля и направлена от положения равновесия (рис. 46).

Если при небольших смещениях тела из первоначального положения равнодействующая приложенных к телу сил остается равной нулю, то тело находится в состоянии безразличного равновесия. В безразличном равновесии находится шар на горизонтальной поверхности (рис. 47).

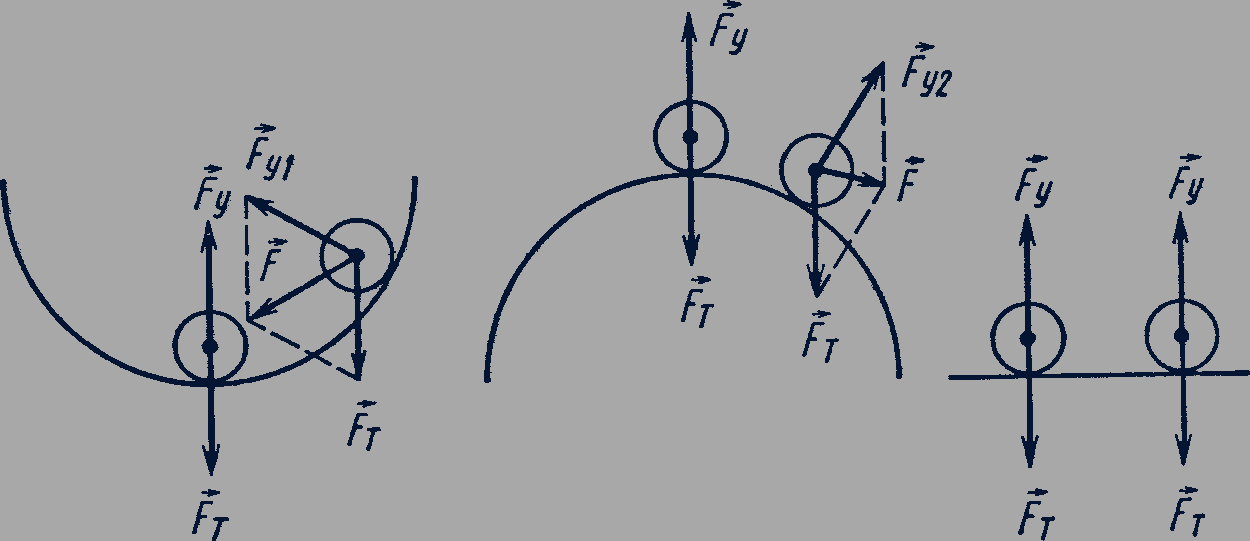
Рис. 45-46-47

Тело, имеющее неподвижную ось вращения, находится в устойчивом равновесии, если его центр тяжести расположен ниже оси вращения и находится на вертикальной прямой, проходящей через ось вращения (рис. 48,а).

При небольшом отклонении от этого положения равновесия алгебраическая сумма моментов сил, действующих на тело, становится отличной от нуля и возникающий момент сил поворачивает тело к первоначальному положению равновесия (рис. 48,б).

Рис. 48

Если же центр тяжести находится на вертикальной прямой, проходящей через ось вращения, но расположен выше оси вращения, то равновесие неустойчивое (рис. 49,а,б).

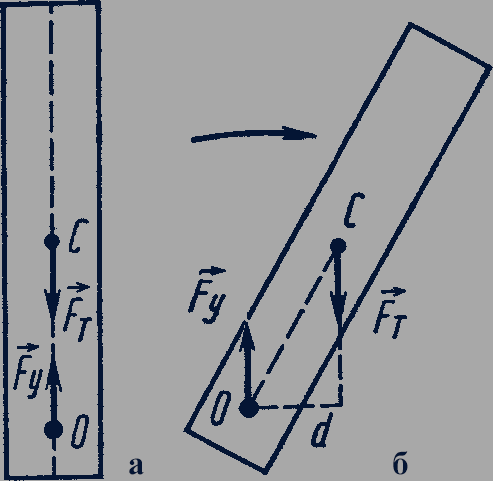
Рис. 49

Тело находится в безразличном равновесии, когда ось вращения тела проходит через его центр тяжести (рис. 50).

Рис. 50

Равновесие тела на опоре. Если вертикальная линия, проведенная через центр тяжести тела, пересекает площадь опоры, то тело находится в равновесии (рис. 51). Если же вертикальная линия, проведенная через центр тяжести, не пересекает площадь опоры, то тело опрокидывается (рис. 52).

Рис. 51-52

15. ЭЛЕМЕНТЫ ГИДРОСТАТИКИ

Давление. При рассмотрении взаимодействий тел не всегда достаточно знать только действующие силы. Во многих случаях важно знать, на поверхность какой площади тела действует сила. Один и тот же человек по снегу идет, глубоко проваливаясь, а надев лыжи, идет, почти не проваливаясь в снег.

Физическую величину, равную отношению модуля силы 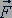, действующей перпендикулярно поверхности, к площади этой поверхности, называют давлением:

. (15.1)

За единицу давления в СИ принято давление, которое производит сила 1 Н на перпендикулярную к ней поверхность площадью 1 м². Эта единица называется паскалем (Па):

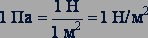Наименование единице давления дано в честь французского ученого Блеза Паскаля (1623-1662).

На практике применяются внесистемные единицы давления: физическая нормальная атмосфера (атм) и миллиметр ртутного столба (мм рт. ст.):

1 атм = 101325 Па = 760 мм рт. ст.

Когда внешние силы действуют на твердые тела, то давление передается в направлении действия силы. Иначе ведут себя при действии внешних сил жидкости и газы.

Закон Паскаля. Паскаль открыл, что все жидкости и газы передают производимое на них давление во все стороны одинаково. Это утверждение называют законом Паскаля.

Свойство жидкостей передавать производимое на них давление одинаково во все стороны наглядно демонстрируется в опыте с шаром Паскаля. При вдвигании поршня в трубку часть воды выталкивается из шара в виде струек, вытекающих по нормали к поверхности шара из всех отверстий, а не только в направлении силы давления поршня (рис. 53).

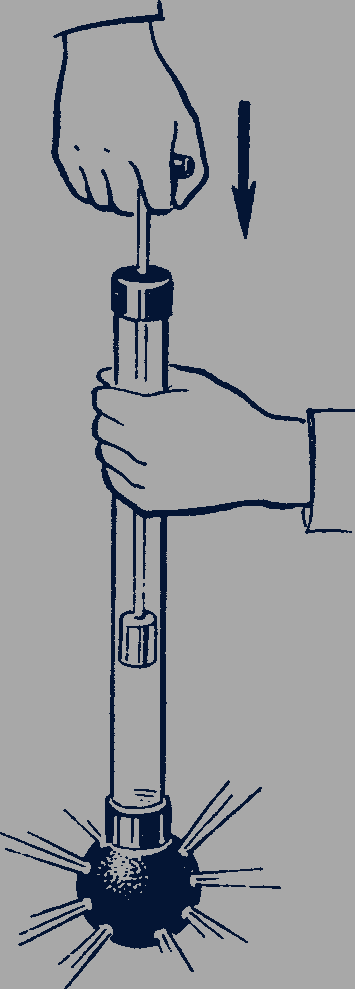
Рис. 53

Гидравлическая машина. На основе использования закона Паскаля работают гидравлические машины. Основными частями гидравлической машины являются два цилиндра с поршнями, в цилиндрах под поршнями находится минеральное масло. Цилиндры соединены между собой трубкой, по которой масло может перетекать из одного цилиндра в другой (рис. 54). Площад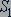и и цилиндров существенно различны, поршни плотно закрывают цилиндры. При действии силы 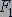на поршень в узком цилиндре с площадью 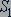в жидкости под поршнем создается давление 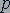, равное

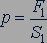Рис. 54

По закону Паскаля такое же давление будет внутри жидкости во втором цилиндре. В результате на поршень во втором цилиндре со стороны жидкости действует сила :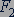

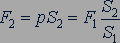Отсюда 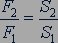. (15.2)

Гидравлическая машина дает выигрыш в силе во столько раз, во сколько площадь ее большого поршня больше площади малого поршня.

Гидравлические машины используются в качестве домкратов для подъема грузов, в прессах для изготовления различных металлических и пластмассовых изделий, в тормозных системах.

Зависимость давления жидкости от высоты столба жидкости. В цилиндрическом сосуде сила давления на дно сосуда равна весу столба жидкости. Давление на дно сосуда равно

Отсюда получаем

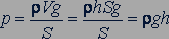. (15.3)

Давление жидкости равно произведению плотности жидкости на модуль ускорения свободного падения 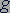и высоту 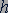столба жидкости.

Такое же давление в соответствии с законом Паскаля жидкость оказывает и на боковые стенки сосуда на глубине .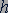

⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨

МЕНЮ САЙТА / СОДЕРЖАНИЕ