Ł Старые понятные учебники советских времен по физике, математике. Акупунктура, похудение

ШВЕЦОВ К.И., БЕВЗ Г.П."СПРАВОЧНИК ПО ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ. АРИФМЕТИКА, АЛГЕБРА", 1965

Первые алгебраические задачи были поставлены и решены еще математиками древнего Египта и Вавилона. Папирус Ахмеса, относящийся к XVIII в. до н.э., содержит решение одиннадцати задач, приводящих к уравнениям с одним неизвестным. Значительно более глубокими знаниями обладали вавилоняне. До нашего времени сохранились тексты с решением системы двух уравнении с двумя неизвестными, квадратных и кубических уравнений, систем квадратных уравнений с двумя и с тремя неизвестными.

В древней Греции алгеброй занимались очень мало. Однако замечательный труд Диофанта Александрийского, написанный около 250 г. н.э., является доказательством того, что в древней Греции уже тогда существовала алгебра как наука, связанная, очевидно, с вавилонской математикой. Этот труд, носивший название "Арифметика", содержал решения задач, приводимых к уравнениям первой и второй степени и к неопределенным уравнениям. Все рассуждения Диофанта - чисто аналитического типа, но при решении каждой задачи он пользовался специальным способом: общих способов решений он не знал. Диофант не знал также отрицательных чисел, а при решении квадратного уравнения давал только положительный корень в качестве ответа. В своих алгебраических рассуждениях он пользовался некоторой символикой.

В истории математики, и в частности алгебры, различают три способа изложения - риторический, синкопированный и символический. Риторическим способом называется такой, когда все предложения записываются словами, символика отсутствует полностью. Этим способом изложения пользовалось большинство математиков вплоть до нового времени.

Синкопированный способ также характеризуется словесной записью математических выражений, однако для часто встречающихся действий и понятий применяется символика. Таким способом выполнен трактат Диофанта, которым вплоть до середины XVII в. пользовались западноевропейские алгебраисты.

Символический способ изложения, при котором математические выражения полностью записываются математическими символами, впервые в Европе был разработан французским математиком Виетом (1540-1603) и применяется со второй половины XVII в. Однако задолго до этого времени он уже применялся индийскими математиками.

Индийцы внесли в алгебру значительный вклад. Во II в. н.э. они пользовались иррациональными числами. В VII в. математик Брахмагупта уже полностью владеет теорией уравнений первой и второй степеней с одним неизвестным. Он пользуется также и понятием отрицательного числа. К XII в. относятся два трактата математика Бхаскары: "Лилавати" и "Биджаганита". В последнем Бхаскара занимается решением квадратных уравнений, причем рассматривает оба корня, считая, однако, второй корень ненужным.

Некоторыми познаниями в алгебре обладали также математики древнего и средневекового Китая. Последняя часть "Математики в девяти книгах", написанной во II-III вв. н.э., посвящена применению алгебры к некоторым задачам геометрии. В XIII в. выдающийся китайский математик Цинь Цзю-Шао написал трактат "Девять отделов искусства счета", в котором он дает численные решения уравнений вплоть до четвертой степени. Это было наивысшим достижением китайцев в области алгебры; дальнейшее развитие математики в Китае последовало лишь в XIX в., после овладения европейскими методами исследования.

Начиная с IX в., алгеброй начали заниматься ученые ряда стран, входивших тогда в состав Арабского халифата. Они пользовались поэтому для своих сочинений арабским языком. Сирийскими, египетскими, иракскими и иранскими учеными были переведены на арабский язык, тщательно изучены и прокомментированы сочинения греческих математиков. Особенно значительный вклад принадлежит среднеазиатским ученым, которые, кроме греческой математики, изучили и индийскую, чем облегчили свои дальнейшие исследования.

Великий хорезмский математик Мухаммед ибн Муса написал трактат под названием "Книга восстановления и противопоставления".

"Восстановлением" Мухаммед называет перенос вычитаемого из одной части уравнения в другую, где оно становится слагаемым; "противопоставлением" - собирание неизвестных в одну сторону уравнения, а известных - в другую сторону. "Восстановление" по-арабски называется "ал-джебр". Отсюда и произошло слово "алгебра". В этом трактате Мухаммед дает учение об уравнениях первой и второй степеней, рассматривает применение алгебры к геометрии, а также к ряду вопросов, связанных с наследованием и делением имущества по сложным законам мусульманского права.

Значение Мухаммеда в истории науки велико. В сущности, он подытожил и свел воедино знания греков, индийцев и среднеазиатских народов по арифметике и алгебре.

Знаменитый таджикский поэт и ученый Омар Хайям (1040-1123) написал около 1070 г. трактат по алгебре, содержащий решение уравнений первой, второй и третьей степеней, а также некоторых специальных видов уравнений методом геометрических построений.

Много алгебраических задач было решено среднеазиатскими и арабскими учеными в связи с развитием астрономии и геометрии. Так, астроном Улуг-Бек (1394-1449) разработал численное решение кубических уравнений типа

𝑥³ + 𝑎𝑥 + 𝑏 = 0,

необходимое для составления тригонометрических таблиц. Его современник ал-Каши разработал правило извлечения корней любой степени из целых чисел. Ал-Каши принадлежит также первое в истории науки применение правила возведения двучлена в любую степень ("бином Ньютона").

В Западной Европе алгебра начала развиваться, начиная с XIII в. В 1202 г. Леонардо Фибоначчи (Леонардо Пизанский) написал "Книгу об абаке", энциклопедическое сочинение, в котором с "ел знания своего времени в области арифметики и алгебры, в значительной степени заимствованные у восточных математиков. Как это сочинение, так и его прообразы - труды среднеазиатских и восточных ученых - написаны чисто риторическим способом и совершенно не содержали символики.

К самостоятельным достижениям Леонардо Фибоначчи относится приближенное алгебраическое решение кубического уравнения.

Точное алгебраическое решение этого уравнения было уже результатом трудов математиков эпохи Возрождения. В сущности, нахождение этого решения явилось одним из тех шагов, которые продвигают науку вперед и дают ей импульс для дальнейшего развития. Поэтому нахождение решения уравнения третьей степени явилось одним из крупнейших достижений математиков XVI в. В 1541 г. итальянский ученый Н. Тарталья нашел общее решение кубического уравнения, но опубликовал его другой итальянский ученый Джеронимо Кардано (1501-1576) в своей книге "Великое искусство". Там же Кардано привел и решение уравнений четвертой степени, найденное его учеником Феррари.

В течение следующих трех веков математики безуспешно искали алгебраические решения уравнений выше четвертой степени и только знаменитый норвежский математик Нильс Генрик Абель (1802-1829) доказал, что общее алгебраическое уравнение выше четвертой степени не разрешимо в радикалах.

В своем труде Кардано указал также, что уравнение третьей степени имеет три корня. Правда, он не дал общего теоретического вывода этого положения, а привел его лишь в нескольких частных случаях. Он впервые решает задачу с комплексными числами: делит 10 на две части, произведение которых равно 40, и в результате получает 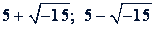. Перемножив эти числа, он получает: 25 + 15 = 40.

Наибольшего развития алгебра как наука достигла в XVI в. во Франции. Труд Франсуа Виета "Введение в аналитическое искусство", опубликованный в 1591 г., был первой из работ в области алгебры, написанной полностью в символической форме. Виет усовершенствовал методы алгебры и тригонометрии и весьма подробно и систематически изложил применение алгебры к геометрии.

При решении уравнений третьей и четвертой степеней он пользовался методом приведения. Однако все корни, кроме положительных, отвергал.

В 1629 г. Жирар (1590-1633) опубликовал свой труд под названием "Новые изобретения в алгебре", где оценил пользу отрицательных корней и установил, что каждое уравнение имеет столько корней, сколько единиц содержится в его показателе степени.

До XVII в. европейские математики, за исключением Жирара, не признавали отрицательных чисел, пока знаменитый французский геометр Рене Декарт (1596-1650) не дал геометрического истолкования их на числовой оси. Однако и после Декарта встречаются неправильные взгляды на отрицательные числа; только с середины XIX в. в учебниках для средней школы отрицательные числа излагаются систематически и дается их правильное истолкование.

Декарт систематизировал также символическую запись алгебраических выражений.

В 1614 г. шотландец Джон Непер (1550-1617) опубликовал теорию изобретенных им таблиц логарифмов. Одновременно с Непером и совершенно независимо от него швейцарец Юст Бюрги составил свои таблицы антилогарифмов - "Арифметические и геометрические таблицы прогрессий", но опубликовал их только в 1620 г. Несколько позже теорию логарифмов развил Бриггс (1556-1630). Знак "log" ввел И. Кеплер в 1624 г.

Значительные исследования в области алгебры принадлежали великому французскому ученому Пьеру Ферма (1601-1665), который разработал прием исключения одного неизвестного из двух уравнений одинаковой степени.

В 1707 г. была опубликована "Универсальная арифметика" И. Ньютона (1642-1727), в которой содержался ряд полученных им результатов из области алгебры. Частично эти результаты были опубликованы несколько раньше, в 1685 г., в "Алгебре" Валлиса (1616-1703). Ньютон усовершенствовал метод исключения Ферма, открыл теорему о биноме, хотя и не дал ее доказательства.

"Алгебра" Джона Валлиса долгое время служила наиболее полным руководством по этому предмету. Кроме глав из области теории и практики алгебры и арифметики, книга содержала также раздел по истории алгебры. В частности, Валлис начал рассматривать степени с отрицательными показателями. Он ввел также знак бесконечности (∞).

Над доказательством биноминальной теоремы в течение XVIII в. работало много выдающихся математиков. Якоб Бернулли (1654-1705) доказал ее, пользуясь теорией сочетаний, для случая целых положительных показателей. Теорема для случая отрицательных и дробных показателей была доказана Леонардом Эйлером (1707-1783). Строгое доказательство было дано лишь в XIX в. Абелем.

На русском языке первой печатной книгой, содержавшей сведения по алгебре, была "Арифметика" Л.Ф. Магницкого. Таким образом, уже с самого начала XVIII в. сведения по алгебре входят в России в состав школьного преподавания.

Л. Эйлер написал "Полное введение в алгебру", которое было переведено на русский язык и издано в 1769 г. под названием "Универсальная арифметика". Книга представляла для своего времени наиболее полное и научно изложенное руководство по алгебре. Особенно хорошо была изложена теория логарифмов, совершенно переработанная Эйлером. Книга была дважды переиздана, а также неоднократно издавалась на немецком и французском языках.

Молодой французский математик Эварист Галуа (1811-1832), погибший в возрасте 21 года, положил основу новому учению в алгебре - теории групп, которое особенно развилось уже в наше время. Однако этот раздел выходит за пределы элементарной алгебры.

В русской школе отдельные сведения из области алгебры излагались в течение всего XVIII в. Сюда относилось учение об уравнениях первой и второй степеней, действия с буквенными выражениями, логарифмы, применение алгебры к решению геометрических задач. С конца XVIII в. под влиянием Эйлера и его учеников в русских учебных заведениях начинает читаться систематический курс алгебры.

Особенно много сделал для постановки преподавания алгебры академик С.Е. Гурьев (1764-1813).

В 1826-1839 гг. издал свою "Ручную математическую энциклопедию" профессор Московского университета Д.М. Перевощиков (1788-1880); третий том этой энциклопедии представлял собой учебник алгебры. Он был дважды переиздан; третье издание вышло в 1854 г. Учебники Д.М. Перевощикова явились значительным вкладом в дело математического, образования в России.

Следует отметить, что вопросами преподавания элементарной математики в средней школе занимались в середине XIX в. такие выдающиеся математики, как Н.И. Лобачевский (1792-1856), М.В. Остроградский (1801-4861), В.Я. Буняковский (1804-1889), О.И. Сомов (1815-1876), П.Л. Чебышев (1821-1894) и другие. Лобачевским и Сомовым, в частности, были составлены учебники по элементарной алгебре для средней школы.

⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨

МЕНЮ САЙТА / СОДЕРЖАНИЕ