Ł Старые понятные учебники советских времен по физике, математике. Акупунктура, похудение

ШВЕЦОВ К.И., БЕВЗ Г.П."СПРАВОЧНИК ПО ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ. АРИФМЕТИКА, АЛГЕБРА", 1965

1. Отношение чисел. Как уже отмечалось, частное от деления одного числа на другое называется также их отношением. Таким образом, частное и отношение обозначают одно и то же понятие. Однако, когда говорят "частное", имеют в виду одно число, полученное в результате деления двух данных чисел. Когда же говорят "отношение", имеют в виду пару чисел, соединенных знаком деления. Например, если разделить 10 на 2, получим 10 : 2 = 5. В данном случае говорят, что частное от деления 10 на 2 равно 5, говорят также, что отношение 10 к 2 равно 5. Но само отношение данных чисел записывают в виде 10 : 2, или 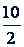. Понятно, что числа 10 : 2 и 5 равны. Поэтому и говорят, что отношение - то же самое, что и частное.

Для обозначения отношения используют дробную черту или двоеточие - знак деления.

Определив величину отношения, получаем ответ на вопрос, во сколько раз одно число больше другого или какую часть другого числа оно составляет.

В общем виде отношение записывают так: 𝑎 : 𝑏.

Числа 𝑎 и 𝑏 называются членами отношения. Первый член 𝑎 называется предыдущим, второй 𝑏 - последующим. Например, в отношении 4 : 5 число 4 есть предыдущий член, 5 - последующий. Из двух чисел можно составить два отношения, например из 7 и 8 имеем: 8 : 7 и 7 : 8. Эти отношения отличаются друг от друга тем, что предыдущий член одного является последующим членом другого и наоборот. Такие два отношения называются обратными. Произведение обратных отношений равно единице:

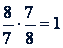
Так как отношение двух чисел получают с помощью деления, то для него справедливы все свойства частного. Основное свойство отношения: величина отношения не изменится, если его члены умножить или разделить на одно и то же число.

Членами отношения могут быть любые числа, только последующий член не может быть равен нулю. Поэтому возможны и такие отношения: 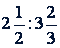, или .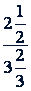

Чтобы получить отношение двух именованных чисел, надо дать эти числа в одних единицах измерения.

Пример. Найти отношения 73 см к 2,92 м.

Решение.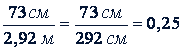

2. Сокращение членов отношения и замена отношения дробных чисел отношением целых чисел. Используя основное свойство отношения, выполняем два преобразования: 1) сокращение членов отношения и 2) замену отношения дробных чисел отношением целых чисел. Как это выполняется, видно из следующих примеров.

Пример 1. Сократить члены отношения: 48 : 32.

Решение. 48 : 32 = 3 : 2.

Пример 2. Заменить отношение дробных чисел отношением целых чисел: .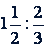

Решение. .

Мы привели дроби к общему знаменателю, а затем умножили предыдущий и последующий члены отношения на их общий знаменатель (на 6).

Примечание. Раньше различали разностные отношения (вида 𝑎 - 𝑏) и кратные отношения (вида 𝑎 : 𝑏). Теперь понятие "разностное отношение" не употребляют. А то, что раньше называли "кратным отношением", называют "отношением".

33. Пропорции

1. Понятие о пропорции. Пропорцией называют равенство двух отношений. Общий вид пропорции: 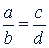, или 𝑎 : 𝑏 - 𝑐 : 𝑑.

Примеры пропорций.

3 : 4 = 9 : 12,

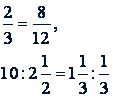
20 м : 4 м = 10 кг : 2 кг.

Пропорции читают так: "3 относится к 4, как 9 к 12", "10 относится к 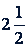, как к 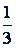" и т.д. Или: "отношение 3 к 4 равно отношению 9 к 12"; "10 во столько раз больше 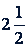, во сколько раз больше ".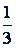

Члены отношений, составляющих пропорцию, называются членами пропорции. Пропорция состоит из четырех членов. Первый и последний члены, т.е. члены, стоящие по краям, называются крайними, а члены пропорции, находящиеся в середине, называются средними членами. Так, в первой пропорции числа 3 и 12 будут крайними членами, а числа 4 и 9 - средними членами пропорции.

Все члены пропорции могут быть абстрактными числами, но два члена одного отношения (или обоих отношений) могут быть и однородными именованными числами:

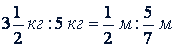
2. Основное свойство пропорции. Произведение крайних членов пропорции равно произведению средних ее членов.

В общем виде это свойство пропорции 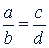записывают так: 𝑎𝑑 = 𝑏𝑐.

Основное свойство пропорции может быть использовано для проверки правильности составленных пропорций.

Пример. Проверить правильность пропорции.

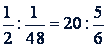
Решение. 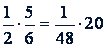. Пропорция правильная, так как выполняется основное свойство пропорции: .

Правильность пропорции может быть проверена также путем вычисления каждого из двух отношений, которые составляют пропорцию.

Пример. Проверить пропорцию .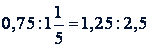

Решение. .

Величина отношений одинакова, следовательно, пропорция составлена правильно.

Итак, из приведенных примеров видно, что если мы напишем такое равенство, у которого в левой части стоит произведение одних двух чисел, а в правой части произведение двух других чисел, то из этих четырех чисел можно составить пропорцию.

3. Вычисление неизвестных членов пропорции. Вычисление неизвестного члена пропорции называют решением пропорции. Для вычисления членов пропорции используются следствия из ее основного свойства.

1) Неизвестный крайний член пропорции равен произведению средних членов, деленному на известный крайний, т.е. если 𝑥 : 𝑎 = 𝑏 : 𝑐, то .

2) Неизвестный средний член пропорции равен произведению крайних членов, деленному на известный средний, т.е., если 𝑎 : 𝑥 = 𝑏 : 𝑐, то .

Пример 1.

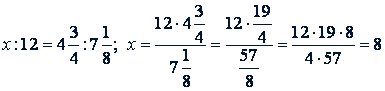
Пример 2.

4. Перестановка членов пропорции. В каждой пропорции можно переставить: а) средние члены, б) крайние члены, в) средние и крайние; г) крайние на место средних и средние на место крайних. Всего можно получить из данной пропорции 8 пропорций (включая данную). В буквенной записи они принимают такой вид:

Для всех этих пропорций выполняется основное свойство: 𝑎𝑑 = 𝑏𝑐.

Пример. Выполнить возможные перестановки членов в пропорции 5 : 3 = 20 : 12.

Решение.

Примечание. Если в пропорции средние или крайние члены равны (такие пропорции называют непрерывными), то из нее можно получить путем перестановки членов только 4 разных пропорций. Например,

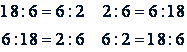
5. Упрощение пропорций. К числу преобразований, не нарушающих пропорцию, относится:

1) одновременное увеличение или уменьшение обоих членов любого отношения в одинаковое число раз;

2) одновременное увеличение или уменьшение обоих предыдущих или обоих последующих членов в одинаковое число раз;

3) одновременное увеличение или уменьшение всех членов пропорции в одинаковое число раз.

Перечисленные преобразования дают возможность упрощать пропорции, в частности освобождать их от дробных членов.

Примеры. Упростить пропорции:

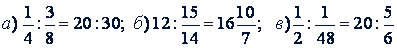
Решение.

а) Приведем дроби к общему знаменателю: 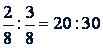. Умножив на 8 оба члена первого отношения, получим: 2 : 3 = 20 : 30.

б) Приведем дроби к общему знаменателю: . Умножив оба последующих члена на 14, получим 12 : 15 = 16 : 20.

в) Умножив все члены пропорции 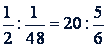на 48, получим 24 : 1 = 960 : 40, или 24 : 1 = 96 : 4.

6. Производные пропорции. Если к обеим частям данной пропорции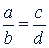

прибавить по 1, то получим

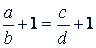
или

Словами это можно выразить так. Сумма членов первого отношения данной пропорции относится к его последующему члену, как сумма членов второго отношения относится к его последующему.

Пример. Если 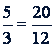, то .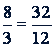

Аналогично из данной пропорции можно получить следующие:

б) ,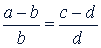

т.е. разность членов первого отношения относится к его последующему члену, как разность членов второго отношения к его последующему члену;

в)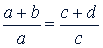

т.е. сумма членов первого отношения относится к его предыдущему члену, как сумма членов второго отношения относится к его предыдущему члену;

г)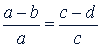

т.е. разность членов первого отношения относится к его предыдущему члену, как разность членов второго отношения относится к его предыдущему члену;

д)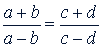

т.е. сумма членов первого отношения относится к их разности, как сумма членов второго отношения относится к их разности;

е)

т.е. сумма предыдущих членов пропорции относится к сумме последующих, как каждый предыдущий к своему последующему.

Все эти и многие другие пропорции, получаемые из данной, называются производными пропорциями.

7. Свойство равных отношений. Последний пример производной пропорции можно обобщить на случай нескольких равных отношений. Если

то

т.е. если несколько отношений равны друг другу, то сумма всех предыдущих их членов так относится к сумме всех последующих, как каждый предыдущий член к своему последующему.

Пример. Если , то .

⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨

МЕНЮ САЙТА / СОДЕРЖАНИЕ