Ł Старые понятные учебники советских времен по физике, математике. Акупунктура, похудение

ШВЕЦОВ К.И., БЕВЗ Г.П."СПРАВОЧНИК ПО ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ. АРИФМЕТИКА, АЛГЕБРА", 1965

17. Арифметические действия над обыкновенными дробями

1. Сложение. Суммой дробей с одним и тем же знаменателем называют дробь, имеющую тот же знаменатель, а числитель равен сумме числителей данных дробей, т.е.

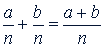
Это определение можно сформулировать также в виде следующего правила.

Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же.

Пример.

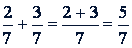Чтобы сложить дроби с разными знаменателями, надо привести их к наименьшему общему знаменателю, а затем сложить полученные числители и под суммой подписать общий знаменатель.

Пример.

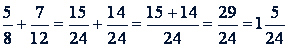
Короче записывают так:

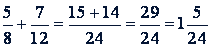
Чтобы сложить смешанные числа, нужно отдельно найти сумму целых и сумму дробных частей. Действие записывается так:

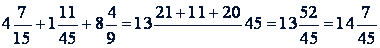
2. Вычитание. Вычитание дробей можно определить как действие, обратное сложению дробей. Вычесть из одного дробного числа второе это значит найти третье число, которое в сумме со вторым дает первое. Из этого определения следует правило:

Чтобы вычесть дроби с одинаковыми знаменателями, нужно вычесть числитель вычитаемого из числителя уменьшаемого и оставить прежний знаменатель. Действие записывают так:

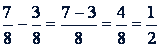
Чтобы вычесть дроби с разными знаменателями, нужно сначала привести их к наименьшему общему знаменателю, затем из числителя уменьшаемого вычесть числитель вычитаемого и под их разностью подписать общий знаменатель. Действие записывают так:

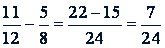
Если нужно вычесть одно смешанное число из другого смешанного числа, то, если можно, вычитают дробь из дроби, а целое из целого. Действие записывают так:

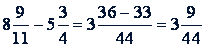
Если же дробь вычитаемого больше дроби уменьшаемого, то берут одну единицу из целого числа уменьшаемого, раздробляют ее в надлежащие доли и прибавляют к дроби уменьшаемого, после чего поступают, как описано выше. Действие записывают так:

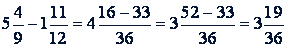
Аналогично поступают, когда надо вычесть из целого числа дробное.

Пример.

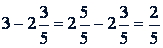3. Распространение свойств сложения и вычитания на дробные числа. Все законы и свойства сложения и вычитания натуральных чисел справедливы и для дробных чисел. Их применение во многих случаях значительно упрощает процесс вычисления.

Пример 1.

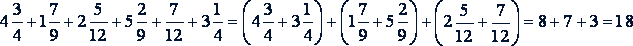Здесь использованы переместительный и сочетательный законы сложения.

Пример 2.

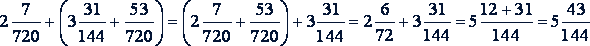Здесь использовано правило прибавления суммы к числу.

Пример 3.

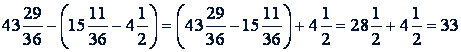Пример 4.

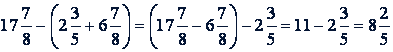Здесь использованы правила вычитания из числа разности и суммы.

4. Умножение. Умножение дроби на целое число можно понимать так же, как и умножение целого числа на целое, т.е. как сложение одинаковых слагаемых. Например,

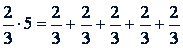Но для умножения на дробь такое толкование не подходит. Например, умножая 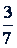на 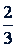, нельзя сказать, что здесь " 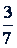надо взять 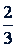раза слагаемым".

Здесь необходимо дать новое определение.

Произведением дробей называют такую дробь, числитель которой равен произведению числителей данных дробей, а знаменатель - произведению их знаменателей, т.е. 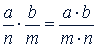. Это определение не является произвольным измышлением. Оно вытекает из необходимости сохранить за действием умножения ту роль, которую оно играло в теории и практике, пока мы рассматривали только целые числа, а также те свойства, которыми обладает умножение целых чисел. В частности, при таком определении те задачи, которые в случае целых числовых данных решаются умножением, в случае дробных числовых данных также можно решать умножением. Из приведенного определения вытекает правило умножения дробей: Чтобы умножить дробь на дробь, нужно умножить числитель на числитель, а знаменатель на знаменатель и первое произведение сделать числителем, а второе - знаменателем: .

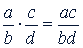При умножении следует делать (если возможно) сокращение.

Пример.

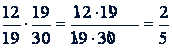Если учесть, что целое число представляет собой дробь со знаменателем 1, то умножение дроби на целое число и целого числа на дробь можно выполнять поэтому же правилу.

Примеры.

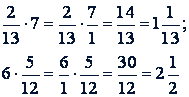
5. Умножение смешанных чисел. Чтобы перемножить смешанные числа, нужно предварительно обратить их в неправильные дроби и потом перемножать по правилу умножения дробей.

Пример.

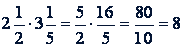Если же перемножают смешанное число на целое, то проще множить отдельно целую часть и дробную часть.

Пример.

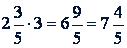
6. Распространение свойств умножения на дробные числа. Свойства умножения натуральных чисел справедливы и для дробей. Их использование упрощает устные и письменные вычисления.

Пример 1.

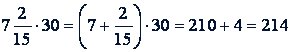Пример 2.

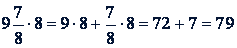Пример 3.

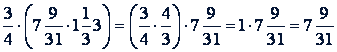Пример 4.

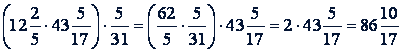7. Деление дробей. Для деления дробей сохраняется то же определение, что и для деления целых чисел: это - действие посредством которого по данному произведению двух сомножителей и одному из этих сомножителей отыскивается второй сомножитель. Разделить одно число на второе - значит найти такое третье число, которое при умножении на второе дает первое. Выполняют деление дробей по следующему правилу.

Чтобы разделить дробь на дробь, нужно числитель первой дроби умножить на знаменатель второй, а знаменатель первой на числитель второй и первое произведение записать числителем, а второе - знаменателем: .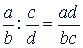

Пример.

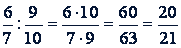По этому же правилу можно выполнять деление дроби на целое число и целого на дробь, если представить целое число в виде дроби со знаменателем 1.

Примеры.

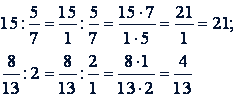
Однако в последнем примере проще числитель разделить на целое число:

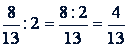
8. Деление смешанных чисел. Чтобы выполнить деление смешанных чисел, их предварительно обращают в неправильные дроби и затем делят по правилу деления дробей.

Пример.

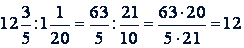Однако при делении смешанного числа на целое бывает удобней делить отдельно целую часть и отдельно дробную часть смешанного числа.

Пример. .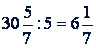

9. Замена деления умножением. Если в какой-нибудь дроби поменять местами числитель и знаменатель, получится новая дробь, обратная данной. Например, для дроби 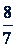обратная дробь будет .

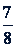Очевидно, что произведение двух взаимно обратных дробей равно 1.

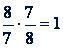Учитывая это, можно деление выполнять по следующему правилу.

Чтобы разделить одно число на другое, нужно делимое умножить на число, обратное делителю.

Пример 1.

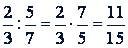Пример 2.

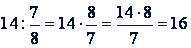
Пример 3.

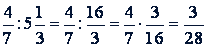10. Примеры на все действия с обыкновенными дробями. Решение примеров на все действия с дробями выполняют с помощью записи по отдельным действиям или записи цепочкой.

Пример. Вычислить:

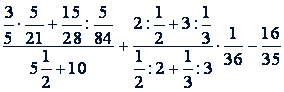
Решение по частям.

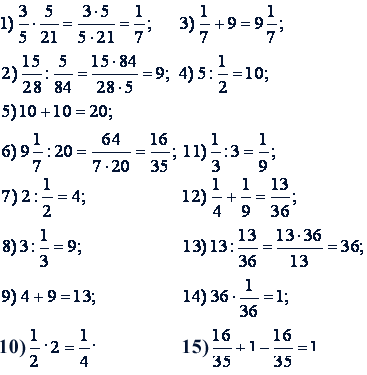
Ответ. 1.

Пример вычисления цепочкой:

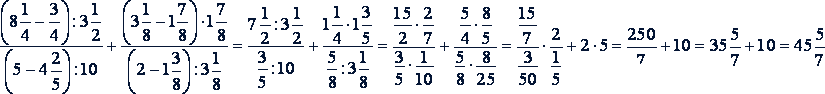
⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨

МЕНЮ САЙТА / СОДЕРЖАНИЕ