
Я создала и активно наполняю телеграм-канал "Перець". Здесь лучшие карикатуры из журнала, начиная с 1922 года.
Заходите, подписывайтесь: https://t.me/cartalana

ШВЕЦОВ К.И., БЕВЗ Г.П."СПРАВОЧНИК ПО ЭЛЕМЕНТАРНОЙ МАТЕМАТИКЕ. АРИФМЕТИКА, АЛГЕБРА", 1965
Умение быстро и безошибочно производить устные и письменные вычисления позволяет экономить труд и время, а также быстро обнаруживать ошибки в своих или чужих расчетах. Приведем несколько способов, которые наиболее часто используются в вычислительной практике..
1. Способы быстрого сложения и вычитания.
Прием округления. Этот прием основан на изменении суммы или разности в зависимости от изменения компонентов и применяется в том случае, когда хотя бы один из компонентов представляет собой число, близкое к круглым десяткам, сотням, тысячам и т.д.
а) Если одно из слагаемых, округляя, увеличим на несколько единиц, то из полученной суммы надо вычесть столько же единиц.
Пример. 264 + 391 = 264 + (391 + 9) - 9 = 264 + 400 - 9 = 655.
б) Если одно слагаемое увеличим на несколько единиц, а второе уменьшим на столько же единиц, сумма не изменится. На основании этого выполняется округление одного слагаемого за счет другого.
Пример. 998 + 936 = 1000 + 934 = 1934.
в) Если вычитаемое при округлении увеличим на несколько единиц, то, чтобы разность не изменилась, надо и уменьшаемое увеличить на столько же единиц.
Пример. 2342 - 996 = 2346 - 1000 = 1346.
г) Если уменьшаемое при округлении уменьшим на несколько единиц, то к полученной разности надо прибавить столько же единиц.
Пример. 10012 - 8645 = 10000 - 8645 + 12 = 1355 + 12 = 1367.
Использование свойств сложения и вычитания.
Примеры.
279 + 583 + 721 = (279 + 721) + 583 = 1583;
352 + 109 - 52 = (352 - 52) + 109 = 409; 573 - 432 - 68 = 573 - (432 + 68) = 73.
2. Способы быстрого умножения и деления.
Умножение методом Ферроля. Для получения единиц произведения перемножают единицы сомножителей, для получения десятков умножаются десятки одного на единицы другого сомножителя и наоборот и результаты складываются, для получения сотен перемножаются десятки (Этот способ умножения следует из тождества (10𝑎 + 𝑏)(10𝑐 + 𝑑) = 100𝑎𝑐 + 10(𝑎𝑑 + 𝑏𝑐) + 𝑏𝑑).
Этот способ можно изобразить схематически так.
Пример.
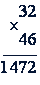
2 · 6 = 12, 2 пишем, 1 помним
3 · 6 = 18, 2 · 4 = 8, 18 + 8 + 1 = 27, 7 пишем 2 помним.
3 · 4 = 12 и 2 - пишем 14.
Умножение на число, близкое к единице какого-нибудь разряда.
Примеры.
405 · 97 = 405 · (100 - 3) = 405 · 100 - 405 · 3 = 40500 - 1215 = 39285;
8012 · 1006 = 8012 (1000 + 6) = 8012000 + 8012 · 6 = 8012000 + 48072 = 8060072.
Умножение на 9, 99 и 999. Чтобы умножить на число, написанное девятками, надо к множимому приписать справа столько нулей, сколько девяток во множителе, и из результата вычесть множимое.
Примеры. 387 · 9 = 3870 - 387 = 3483; 24 · 99 = 2400 - 24 = 2376; 18 · 999 = 18000 - 18 = 17982.
Умножение двузначного числа на 11. Чтобы умножить двузначное число, сумма цифр которого меньше 10, на 11, надо между цифрами числа написать сумму его цифр.
Пример. 72 · 11 = 792.
Чтобы умножить на 11 двузначное число, сумма цифр которого больше или равна 10, надо между цифрой десятков, увеличенной на 1, и цифрой единиц написать избыток суммы цифр числа над 10.
Пример. 68 · 11 = 748.
Умножение на 5, 25, 125. Чтобы умножить число на 5, 25, 125, достаточно разделить его соответственно на 2, 4, 8 и результат умножить на 10, 100, 1000.
Примеры.
2486 · 5 = 12430, так как 2486 : 2 = 1243;
8084 · 25 = 202100, так как 8084 : 4 = 2021.
Деление на 5, 25, 125 Чтобы разделить число на 5, 25, 125, достаточно умножить его соответственно на 2, 4, 8 и разделить на 10, 100, 1000.
Примеры.
235 : 5 = 47, так как 235 · 2 = 470;
1175 : 25 = 47, так как 1175 · 4 = 4700.
Использование свойств умножения и деления
Примеры.
93 · 8 · 125 = 93 · (8 · 125) = 93000;
36 · 18 : 9 = 36 · (18 : 9) = 36 · 2 = 72;
26 · 235 : 13 = (26 : 13) · 235 = 470.
Возведение в квадрат чисел, имеющих цифру 5. Чтобы возвести е квадрат двузначное число, оканчивающееся цифрой 5, достаточно число его десятков умножить на число, увеличенное на единицу, и к произведению справа дописать 25.
Пример. Вычислить 352.
Решение (выполняется устно). 3 · 4 = 12, дописав 25, получим результат: 352 = 1225.
Чтобы возвести в квадрат двузначное число, имеющее 5 десятков, достаточно к 25 прибавить цифру единиц и к результату приписать справа квадрат числа единиц так, чтобы в результате получилось четырехзначное число (Эти правила следуют из тождеств: (10𝑎 + 5)2 = 100𝑎 (𝑎 + 1) + 25, (50𝑎 + 𝑏) = 2500 + 100𝑏 + 𝑏2).
Пример. Вычислить 542; 522.
Решение (выполняется устно). К 25 прибавляем 4, получаем 29. Приписываем 16. Получаем: 542 = 2916.
522 = 2704.
8. Инструментальные вычисления
Кроме устных и письменных вычислений, широкое распространение получили также различные инструментальные вычисления, т.е. вычисления с помощью специальных приспособлений - счетов, арифмометров и т.п.
1. Русские счеты. Это приспособление представляет собой деревянную раму с параллельными проволоками (обычно их 15). На каждой проволоке, нанизано по 10 косточек, на четвертой или на третьей снизу - четыре косточки. Для удобства две средние косточки на каждой проволоке окрашены в черный цвет (рис. 1).

Рис. 1
На счетах разрядные единицы заменяются косточками, которые откладываются на соответствующих проволоках. Целое число изображается при помощи косточек в таком же порядке, как и на письме, начиная с единиц высшего разряда числа, последовательно разряд за разрядом, вплоть до простых единиц.
При откладывании чисел на счетах пользуются следующими правилами: а) 10 косточек на любой проволоке счетов заменяются одной косточкой соседней верхней проволоки, а одна косточка на любой проволоке может заменяться десятью косточками соседней нижней проволоки; б) на определенных проволоках счетов надо откладывать лишь столько косточек, сколько единиц содержит соответствующий разряд данного числа; в) проволоки счетов, соответствующие тем разрядам, где в записи данного числа стоит нуль, надо оставлять свободными.
Для того чтобы сложить два числа, следует отложить на счетах первое слагаемое, затем - второе. Если при откладывании второго слагаемого на какой-нибудь проволоке не хватает косточек, следует отложить одну косточку на проволоке следующего высшего разряда, одновременно сняв (слева) на данной проволоке столько косточек, сколько единиц соответствующего разряда не хватает во втором слагаемом до 10. Отложив на счетах второе слагаемое, получим результат - сумму двух слагаемых. Если нужно сложить три или больше слагаемых, то к сумме первых двух прибавляют третье и т.д.
Например. 235 + 387. Отложив на счетах 235 (слева), присоединим к 2 косточкам разряда сотен еще 3, получим 5 сотен. На следующей нижней проволоке следует отложить влево 8 косточек, но там их только 7, поэтому вместо 8 десятков отложим на следующей верхней проволоке 1 сотню, т.е. 10 десятков и сбросим на данной проволоке 2 косточки (2 десятка, которые мы отложили лишние). Чтобы прибавить 7 единиц, прибавим 1 десяток, а 3 единицы снимем. Получим 622.
При вычитании на счетах надо отложить уменьшаемое и с него сбросить вычитаемое.
При этом: а) сбрасывание косточек начинают с единиц старшего разряда; б) если в процессе вычитания на какой-нибудь проволоке для сбрасывания соответствующего разрядного числа вычитаемого не хватает косточек, то на этой проволоке переводят влево число косточек, дополняющее число разрядных единиц вычитаемого до 10, а на ближайшей сверху проволоке сбрасывают одну косточку; в) по оставшимся слева косточкам, читают разность.
Умножение чисел на счетах приводится к сложению. Но приведение умножения к сложению на счетах практически оправдывает себя только тогда, когда пользуются сокращенными способами умножения. Наиболее распространенный способ основан на умножении одного из сомножителей на сумму разрядных единиц второго сомножителя с последовательным сложением полученных произведений.
Например, 123 · 12 = 123 · 10 + 123 · 2 = 1230 + (123 + 123).
Часто используется также прием округления.
Деление на счетах сводится к последовательному вычитанию из делимого делителя и его произведений на целые степени десяти. При этом в каждом разряде частного будет столько единиц, сколько раз пришлось вычитать произведения делителя на соответствующую степень 10. Исчерпывание делимого следует начинать со старших разрядных единиц. При делении верхние проволоки отводят для изображения частного.
Например, пусть требуется разделить 9375 на 75. Для этого откладываем на счетах 9375, затем отделяем большим пальцем левой руки в делимом 93, из 93 вычитаем (сбрасываем) делитель 75 : 93 - 75 = 18. В частном (на крайней верхней проволоке) откладываем одну кость. Передвигаем большой палец левой руки вниз на одну проволоку. Из числа 187 два раза вычитаем число 75, в частном на одну проволоку ниже откладываем две кости. Из оставшегося числа 375 вычитаем пять раз число 75; каждое вычитание отмечаем одной костью в частном на третьей сверху проволоке. После этого в делимом не будет остатка, а в частном будет отложено 125. Это будет искомый результат.
2. Арифмометр. Существует много различных типов арифмометров (Г.П. Евстигнеев и В.Н. Криушин, Счетно-цифровые машины, Машгиз, 1953). Мы рассмотрим арифмометр "Феликс" (рис. 2).
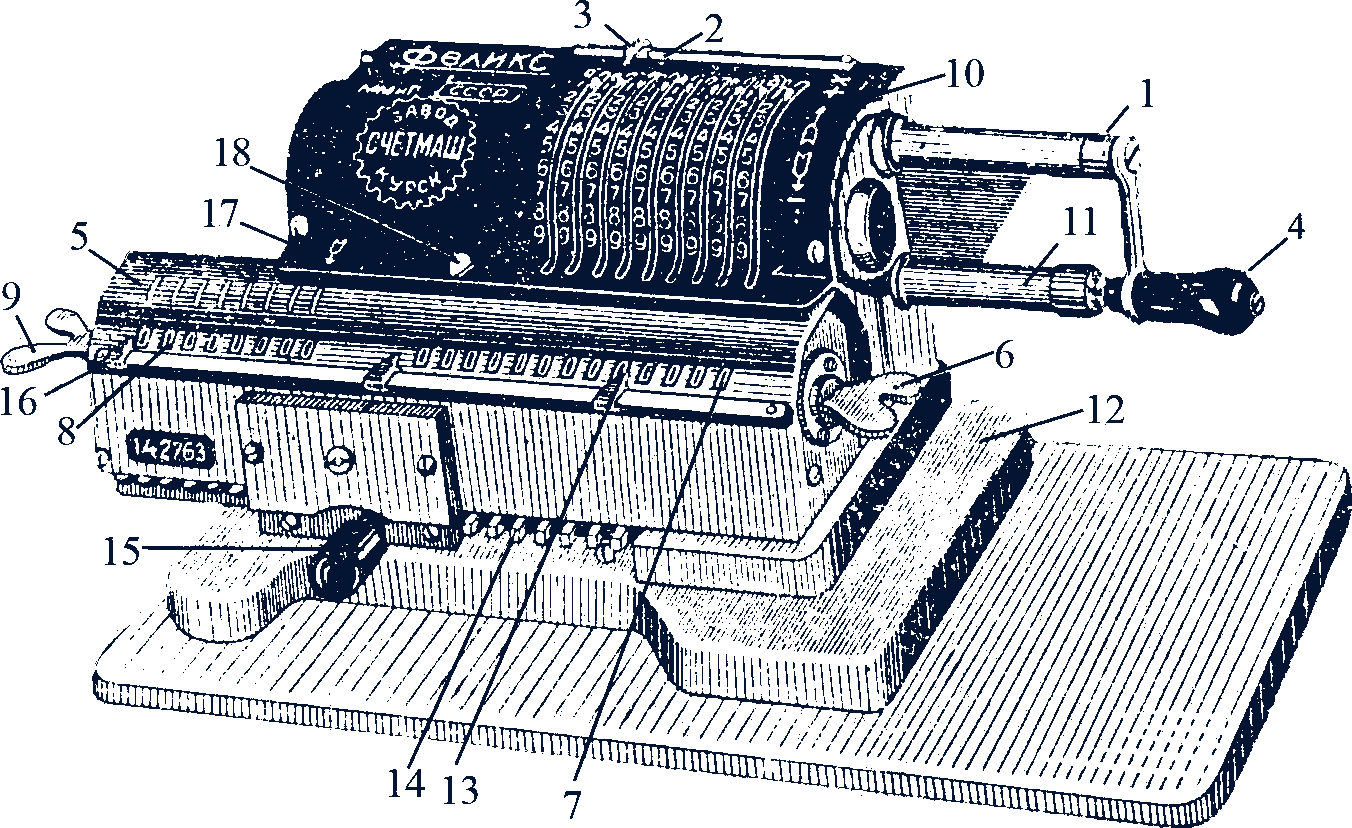
Рис. 2
Установка чисел на этом арифмометре осуществляется передвижением установочных рычагов 2 вниз по установочным шкалам. Всего установочных шкал 10, каждая из них соответствует определенному разряду. Нумерация установочных шкал идет справа налево и воспроизведена на специальной шкале.
Чтобы привести все установочные рычажки в исходное положение (погасить установку), необходимо повернуть на четверть оборота по часовой стрелке оперативную рукоятку 4 при отведенной влево кнопке гасительной гребенки рычажков 18.
В каретке 5 арифмометра находятся окна счетчиков: справа окна счетчика результатов 7 и слева окна счетчика оборотов 8. В счетчике результатов имеются 13 разрядов (окошек), в счетчике оборотов - 8. Разряды результативного и оборотного счетчиков занумерованы справа налево. При вращении оперативной рукоятки в окошках оборотного счетчика появляются цифры (белые при вращении по часовой стрелке, красные при вращении против часовой стрелки), указывающие число соответствующих оборотов. Счетчики гасятся гасительными барашками 6 и 9, при помощи поворота их до защелкивания.
При одном нажиме на рычажок 15 каретка может переместиться только на один разряд в соответствующем направлении. При поднятом рычажке 15 каретка может свободно перемещаться вправо и влево.
Для указания разряда, в котором идет счет, служит стрелка 17. Подвижные запятые служат для отделения целой части чисел, которые получаются на счетчиках, от дробной части.
Перед началом работы на арифмометре необходимо его привести в исходное положение, т.е.:
а) оперативная рукоятка 4 должна быть опущена вниз и защелкнута;
б) барашки 6 и 9 горизонтально и защелкнуты;
в) каретка 5 неподвижна и защелкнута рычажком 15;
г) оба счетчика погашены.
Во время вращения оперативная рукоятка 4 должна быть оттянута вправо, а по окончании вращения защелкнута. Вращать рукоятку надо с остановкой внизу. Барашки, рукоятка и установочные рычажки должны работать легко.
При работе на арифмометре запрещается:
а) вращать рукоятку, не убедившись в том, что барашки защелкнуты;
б) останавливать рукоятку не в вертикальном нижнем положении;
в) перемещать каретку, не проверив, что барашки и рукоятка защелкнуты;
г) делать резкие движения и удары по рычагу при перемещении каретки на несколько делений.
Сложение на арифмометре. Пусть требуется сложить два числа: 38785 и 30817. Для этого поступаем таким образом:
1) приводим арифмометр в исходное положение;
2) ставим каретку в крайнее левое положение;
3) установочными рычажками набираем первое слагаемое 38785, - единицы на первой шкале, десятки на второй и т.д.;
4) оперативной рукояткой 4 делаем полный оборот по часовой стрелке; в окошках результативного счетчика появляется первое слагаемое (38785), в окошке оборотного счетчика - белая цифра 1;
5) отводим влево рычажок гасительной гребенки и делаем четверть оборота по часовой стрелке, гасим на установочных шкалах первое слагаемое;
6) не сдвигая каретку, устанавливаем рычагами второе слагаемое (30817);
7) делаем полный оборот оперативной рукоятки по часовой стрелке;
8) в окошках результативного счетчика читаем сумму (69602).
При сложении трех или большего количества слагаемых повторяем пятую, шестую и седьмую операции и только после этого читаем результат.
Вычитание. Пусть требуется из числа 38785 вычесть число 30817. Для этого проделываем шесть первых операций, которые следовало бы сделать при сложении указанных чисел, а затем в качестве 7-й операции делаем полный оборот оперативной рукоятки против часовой стрелки и в качестве 8-й операции, так же как и в случае сложения, на результативном счетчике читаем разность (7968).
Умножение. Пусть требуется найти произведение 654 · 56. Для этого делаем следующее:
1) приводим арифмометр в исходное положение;
2) ставим каретку в крайнее левое положение;
3) устанавливаем рычажками сомножитель с большим числом значащих цифр (654);
4) вращаем оперативную рукоятку по часовой стрелке 6 раз (до появления в окошке оборотного счетчика низшего разряда второго сомножителя;
5) передвигаем каретку на один разряд и вращаем рукоятку по часовой стрелке 5 раз (до появления во втором окошке оборотного счетчика следующей справа налево цифры второго сомножителя);
6) на результативном счетчике читаем произведение (36624).
Если бы во втором множителе была цифра третьего разряда, то 5-ю операцию следовало бы повторить. Так же следовало бы поступить при наличии во втором множителе цифр четвертого и высших разрядов.
Примечание. При перемножении десятичных дробей, прежде чем считать результат, следует произвести отделение целой части произведения от дробной при помощи запятой 13 на шкале счетчика результатов.
При выполнении в каком-либо разряде умножения на число, большее пяти, имеет смысл для сокращения числа оборотов сделать один лишний положительный оборот в соседнем слева разряде, а в разряде, производимом умножение, сделать отрицательные обороты в количестве, равном разности 10 и числа, на которое производится умножение.
Например, при умножении на 187 можно обойтись шестью оборотами (вместо 16): тремя отрицательными оборотами в разряде единиц, одним отрицательным в разряде десятков и двумя положительными в разряде сотен (200 - 13). На счетчике оборотов будет число 213, причем 2 - белая цифра, 1 и 3 - красные цифры. Читать это число следует так: 200 - 13 = 187 (число оборотов, равное множителю).
Деление. Операция деления на арифмометре, так же как и на русских счетах, приводится к повторному вычитанию делителя из делимого, в результате чего в счетчике оборотов получается частное.
Пусть требуется произвести на арифмометре деление 624 : 24.
Для этого поступаем так:
1) приводим арифмометр в исходное положение;
2) подаем каретку вправо до отказа (а не влево, как при умножении);
3) устанавливаем делимое 624 при помощи оперативной рукоятки 4, каретки 5 и гасительного барашка 6;
4) прямым оборотом оперативной рукоятки переводим делимое в счетчик результатов, где оно расположится в окошках: 6 в 13-и окошке, 2 в 12-м окошке и 4 в 11-м окошке;
5) гасим единицу, получившуюся в окне счетчика оборотов 8, и установочные рычажки;
6) устанавливаем рычажками при помощи каретки 5 и гасительного барашка счетчика результатов 6 делитель 26 против 62 делимого;
7) делаем два обратных оборота рукоятки, после чего на месте первых двух цифр делимого появляется 10, а в счетчике оборотов - красная цифра 2;
8) подаем каретку на один разряд влево и делаем четыре обратных поворота. В счетчике результатов появляются нули, а в счетчике оборотов - частное 24 (красными цифрами). Следовательно, 624 : 26 = 24.
⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨
МЕНЮ САЙТА / СОДЕРЖАНИЕ