Ł Старые понятные учебники советских времен по физике, математике. Акупунктура, похудение

ЧЕРТОВ А.Г. "ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН", 1977

Температура по термодинамической и Международной практической температурным шкалам может быть выражена как в Кельвинах, так и в градусах Цельсия. В соответствии с этим различают четыре температуры:

термодинамическая температура Кельвина выражается в Кельвинах (К); обозначается символом Т;

термодинамическая температура Цельсия, выражается в градусах Цельсия (°С); обозначается символом t;

международная практическая температура Кельвина, выражаемая в Кельвинах (К); обозначается символом Т₆₈ *;

международная практическая температура Цельсия, выражаемая в градусах Цельсия (°С); обозначается символом t₆₈.

Для перехода от одной температуры к другой установлены соотношения:

t = T - Т₀, t₆₈ = T₆₈ - T₀, (14.5)

где T₀ = 273,15 К.

* В обозначении международной практической температуры индекс "68" может быть опущен, если это не вызывает недоразумений.

Единица количества вещества - моль

Решением XIV Генеральной конференции по мерам и весам (1971 г.) единица количества вещества - моль была утверждена в качестве седьмой основной единицы Международной системы.

В Государственном стандарте "Единицы физических величин" дано следующее определение:

"Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде-12 массой 0,012 кг. При применении моля структурные элементы должны быть специфицированы и могут быть атомами, молекулами, ионами, электронами и другими частицами или специфицированными группами частиц".

Понятие "количество вещества" было введено в науку давно. Однако считалось, что количество вещества не является особой самостоятельной величиной, принципиально отличной от массы. Хотя после предположения Авогадро (1813 г.) о том, что равные объемы различных газов при одинаковом давлении содержат одно и то же число молекул, количество вещества и трактовалось как число молекул, но будучи пропорциональным массе, оно тождественно ей. Представление о тождественности количества вещества и массы во многом опиралось на убеждение в том, что все молекулы (атомы) данного вещества во всех отношениях тождественны, что их масса постоянна и, следовательно, масса тела или системы пропорциональна числу содержащихся в них молекул. Собственно, и о числе молекул можно было судить только по массе тела, так как не существовало прямых способов определения числа молекул.

Открытия в области физики в первой половине двадцатого столетия поколебали убеждение в тождественности массы и количества вещества.

Как известно из квантовой теории, атомы и молекулы могут пребывать в различных стационарных состояниях. Причем энергия атомов и молекул, находящихся в различных состояниях, разная. В соответствии же с теорией относительности масса любого материального объекта, в том числе атомов и молекул, пропорциональна энергии Е в этом объекте, т.е.

m = Е/с2,

где с - скорость электромагнитных волн в вакууме.

Следовательно, массы молекул одного и того же вещества, находящихся в разных стационарных состояниях, различны и поэтому масса тела (системы) не пропорциональна числу молекул. Отсюда следует вывод о том, что количество вещества есть величина, принципиально отличная от массы.

Единица количества вещества - моль также была известна еще в XIX в. Но до недавнего времени моль рассматривался как индивидуальная единица массы. Индивидуальная в том смысле, что размер этой единицы для каждого вещества был особый. Слово "моль" происходит от латинского слова "moles" и означает количество, массу или счетное множество. Из этих трех понятии последнее - счетное множество точнее всего выражает современное понимание моля.

В определении моля не указывается точное число содержащихся в нем структурных элементов. Принято считать его равным числовому значению постоянной Авогадро N_A.

Но при установлении значения постоянной Авогадро различными методами результаты не согласуются между собой с необходимой точностью. По данным на 1973 г. ее наиболее достоверное значение

N_А = (6,022045 ± 0,000031) · 10²³ моль^-1.

Следовательно, моль вещества соответствует числу (6,022045 ± 0,000031) · 10²³ структурных элементов.

Если система содержит различные структурные элементы, то общее их число N можно выразить как сумму

N = N₁ + N₂ +...+ N_i, (14.6)

где N_i - число структурных элементов i-й группы, входящей в систему. Разделив обе части этого равенства на постоянную Авогадро получим количество вещества этой системы в молях:

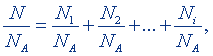
или

ν = ν₁ + ν₂ +...+ ν_i, (14.7)

где ν_i - количество вещества i-й группы структурных элементов.

Эталона моля еще не существует. С развитием экспериментальной техники открываются возможности для определения числа частиц методами, не связанными с измерением массы. Это позволит создать эталон для хранения и воспроизведения моля.

Единица количества вещества - моль в настоящее время широко применяется. Ею пользуются в химии для расчета количества вещества, участвующего в реакциях, в молекулярной физике для определения газовых параметров при различных процессах. На основе моля образован ряд величин, выражаемых через количество вещества: молярная масса, молярный объем, молярная теплоемкость, молярная проводимость и др.

Единица силы света - кандела

Первоначально кандела * определялась как сила света стеариновой, спермацетовой или парафиновой свечи определенной массы или сила света лампы накаливания и др.

* Это наименование происходит от латинского слова "candela" - свеча. До 1970 г. в государственных стандартах СССР единица силы света именовалась свечой.

В 1881 г. Международным конгрессом электриков в качестве единицы силы света была принята одна двадцатая часть силы света, излучаемого квадратным сантиметром поверхности затвердевающей платины в направлении, нормальном к поверхности. Однако в связи с трудностями осуществления платинового эталона единицы силы света только в 1948 г. по постановлению Международного комитета мер и весов был практически совершен переход к новой единице, устанавливаемой с помощью платинового излучателя.

Платиновый излучатель показан на рис. 4. В расплавленную платину 1, находящуюся в сосуде 2, помещена трубка 3, стенки которой, выполненные из плавленой окиси тория, служат излучателем. Сосуд с расплавленной платиной вставлен во внешний сосуд 4, заполненный в качестве теплоизолятора окисью тория 5. Выходное отверстие трубки 3 может быть принято за полный излучатель.

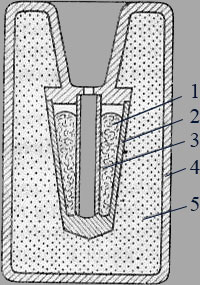
Рис. 4

В соответствии с решением XIII Генеральной конференции по мерам и весам (1967 г.) кандела получила определение:

"Кандела - сила света, испускаемого с площади 1/600 000 м² сечения полного излучателя в перпендикулярном к этому сечению направлении при температуре излучателя, равной температуре затвердевания платины при давлении 101 325 Па".

При температуре затвердевания платины (2042 К) яркость черного излучателя В = 6·10⁵ кд/м². Но так как сила света связана с яркостью соотношением

I = BS, (14.8)

то после подстановки приведенных значений В и S получим

I = 6·10⁵ кд/м² · 1/600 000 м² = 1 кд.

Кандела по размеру несколько меньше применявшейся до 1948 г. "Международной канделы". Между ними существует соотношение

1 кд (межд.) = 1,005 кд.

Государственный первичный эталон канделы СССР состоит: 1) из полного излучателя; 2) аппаратуры для нагрева и возбуждения излучателя; 3) установки дли передачи размера канделы вторичным эталонам. Точность современного эталона канделы определяется относительной погрешностью

Единица плоского угла - радиан

Радиан равен углу между двумя радиусами окружности, длина дуги между которыми равна радиусу.

Исходя из этого определения, любой центральный угол, выраженный в радианах, может быть представлен как отношение длины дуги, на которую опирается центральный угол, к радиусу окружности:

φ = s/R. (14.9)

Из этой формулы следует, что плоский угол имеет нулевую размерность в любой системе единиц.

За последние годы в станкостроении, приборостроении, при освоении космоса возросли требования к точности измерения плоских углов. Возникла необходимость измерять плоские углы с точностью до десятых долей угловой секунды. В связи с этим и в целях обеспечения единства измерений плоских углов в СССР был разработан и введен Государственный первичный эталон единицы плоского угла.

Эталон плоского угла основан на том, что сумма всех центральных смежных углов многогранной призмы составляет 2π радиан (360°). Эталон состоит из 36-гранной призмы, эталонной угломерной установки и установки для поворота многогранной призмы.

Выбор радиана в качестве единицы Международной системы нельзя признать удачным. Радиан мало пригоден для практических целей. Полный и прямой углы, постоянно встречающиеся как в теории, так и на практике, выражаются в радианах иррациональными числами (2π и π/2). Поэтому на практике для измерения плоских углов пользуются внесистемной единицей - градусом и недесятичными дольными от него единицами - минутой и секундой.

Поиски удобных единиц плоского угла начаты давно и продолжаются по настоящее время. Были предложения за единицу плоского угла принять 1/100, 1/3000 и 1/3600 часть прямого угла, или 1/600 и 1/1000 часть полного угла и т.д. Однако все эти предложения сводились к введению внесистемных единиц плоского угла и не решали задачу включения единицы плоского угла в число когерентных единиц Международной системы.

Единица телесного угла - стерадиан

Телесным углом называют часть пространства, ограниченную конической поверхностью с замкнутой направляющей (рис. 5). Размер телесного угла определяется отношением площади S поверхности вырезаемой конической поверхностью на сфере с центром в вершине этой поверхности, к квадрату радиуса R сферы:

ω = S/R². (14.10)

Из этой формулы следует, что телесный угол - величина безразмерная и, следовательно, выражается в безразмерных единицах. Этой безразмерной единице присвоено название стерадиан (ср).

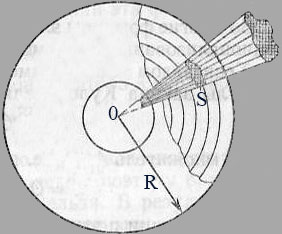
Рис. 5

Стерадиан равен телесному углу с вершиной в центре сферы, вырезающему на поверхности сферы площадь, равную площади квадрата со стороной, равной по длине радиусу сферы.

Замечания, сделанные выше о радиане, относятся и к стерадиану: он не удобен для практических целей, поскольку находится в иррациональном отношении с полным телесным углом. Разделив площадь S поверхности сферы на квадрат ее радиуса R, получаем выражение полного телесного угла в стерадианах:

ω = S/R² = 4πR²/R² = 4π.

В заключение отметим, что основу для установления единства измерений физических величин составляют эталоны не только основных, но и производных единиц. В настоящее время разработаны и утверждены государственные первичные эталоны СССР многих производных единиц: плотности жидкости, давления, температурного коэффициента линейного расширения твердых тел, электрической емкости, электродвижущей силы, индуктивности, массы радия и др. Эталоны производных единиц - в большинстве своем сложные установки. Описание их выходит за рамки данного пособия.

§ 15. РАЦИОНАЛИЗАЦИЯ УРАВНЕНИЙ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

В § 9 было указано, что в Международной системе единиц применяются уравнения электромагнетизма в рационализованной форме. Сущность рационализации состоит в следующем.

Во многие формулы электромагнетизма, записанные в нерационализованной форме, входят множители 4π и 2π. О. Хевисайдом было подмечено, что если в знаменатель формулы закона Кулона для электрических зарядов

F = Q₁Q₂/(ε₀εr²)

ввести множитель 4π, т.е. записать этот закон в виде

F = Q₁Q₂/(4πε₀εr²)

и в соответствии с этим изменить другие формулы электромагнетизма, то множители 4π и 2π исчезнут из тех формул, которые наиболее часто встречаются на практике.

Такое преобразование уравнений, произведенное с целью упрощения наиболее употребительных формул, получило название рационализация уравнений электромагнитного поля. Однако значение рационализации не исчерпывается только упрощением формул. В результате рационализации многие формулы электромагнетизма становятся более совершенными: формулы, присутствие в которых множителей 4π и 2π нельзя логически объяснить, освобождаются от них, и, наоборот, формулы, в которых наличие этих множителей может быть оправдано, приобретают их. Например, электростатическое поле, созданное точечным зарядом, обладает сферической симметрией. Геометрическое место точек равного потенциала такого поля представляет собой сферу. И естественно, чтобы в формулу, выражающую потенциал поля точечного заряда, входил множитель 4π, численно равный площади поверхности сферы единичного радиуса. Однако формула потенциала точечного заряда в классической нерационализованной форме не содержит этого множителя и имеет вид

φ = Q/(ε₀εr).

В рационализованной форме это уравнение записывается так:

φ = Q/(4πε₀εr).

Емкость уединенного проводника зависит от его формы, поэтому в формулу емкости шара должен входить множитель 4π. Однако в нерационализованной форме емкость уединенной проводящей сферы выражается уравнением

С = ε₀εR.

В результате рационализации уравнений эта формула приобретает вид

С = 4πε₀εR.

Формула емкости плоского конденсатора в нерационализованной форме

C = ε₀εS/(4πd)

содержит множитель 4π, хотя поле плоского конденсатора сферической симметрией не обладает, и поэтому объяснить присутствие здесь множителя 4π нельзя. В результате рационализации уравнений электромагнетизма этот множитель из формулы емкости плоского конденсатора исчезает и она приобретает вид

C = ε₀εS/d.

Аналогично дело обстоит и с многими другими формулами (см. табл. 10). Как уже было указано выше, рационализация уравнений электромагнетизма начинается с введения множителя 4π в знаменатель закона Кулона. Для двух одинаковых зарядов Q, помещенных в вакуум, закон Кулона имеет вид *:

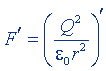в нерационализованной форме; (15.1)

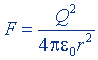в рационализованной форме. (15.2)

* Условимся величины, входящие в нерационализованные уравнения, записывать штрихованными символами.

Но так как формулы (15.1) и (15.2) выражают одну и ту же силу, то, приравняв правые части этих формул и сократив на r², получим *

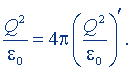(15.3)

* Механические величины - сила F, длина r как установленные ранее независимо от электрических и магнитных величин не должны изменяться при рационализации уравнений электромагнетизма.

Для выполнения этого равенства необходимо, чтобы числовое значение заряда в рационализованной форме увеличилось в 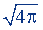раз или чтобы электрическая постоянная уменьшилась в это же число раз.

Если условиться, чтобы при рационализации закона Кулона заряд как физическая величина и его единица - кулон не изменялись, т.е. если считать, что

Q = Qʹ,

то из равенства (15.3) следует

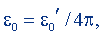(15.4)

т.е. в результате рационализации электрическая постоянная уменьшилась в 4π раз. В этом случае говорят, что рационализация закона Кулона произведена за счет рационализации электрической постоянной ε₀.

Если, наоборот, условиться, чтобы при рационализации закона Кулона неизменной оставалась электрическая постоянная, т.е. если 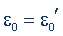, то из формулы (15.3) следует

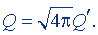
Последнее равенство в соответствии с формулой (1.1) можно представить в виде

(15.5)

Если считать, что числовые значения зарядов в результате рационализации не меняются, т.е. если

{Q} = {Qʹ},

то из формулы (15.5) следует

т.е. в результате рационализации единица заряда должна увеличиваться в 4π раз. В этом случае говорят, что рационализация закона Кулона произведена за счет рационализации единицы заряда.

Если же положить

[Q] = [Qʹ],

т.е. если считать, что при рационализации остается неизменной единица заряда, то из (15.5) следует

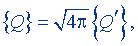
т.е. изменяется числовое значение заряда. Но если две величины Q и Qʹ , будучи выраженными в одних и тех же единицах, имеют разные числовые значения, то это значит, что сами эти величины разные, и, следовательно, при рационализации закона Кулона произошло изменение понятия заряда как физической величины. В этом случае говорят, что рационализация закона Кулона произведена за счет рационализации заряда.

Итак, рационализацию закона Кулона можно произвести путем рационализации: а) заряда; б) единицы заряда - кулона; в) электрической постоянной. В соответствии с соглашением, достигнутым в международных организациях, при рационализации уравнений электромагнитного поля не должно допускаться изменение понятий и размера единиц важнейших величин, в том числе и заряда. Поэтому полагают, что рационализацию закона Кулона следует произвести за счет рационализации электрической постоянной ε₀, при которой ее значение уменьшается в 4π раза по сравнению с прежним. Так как при нерационализованной форме уравнений

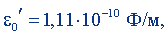
то при рационализованной форме уравнении в этой же системе

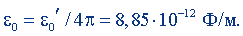
Изменение числового значения электрической постоянной позволяет при рационализации сохранить неизменным, кроме кулона, следующие важнейшие электрические единицы: силы тока - ампер, напряжения - вольт, электрической емкости - фараду, напряженности электрического поля - вольт на метр, а также магнитные единицы: магнитной индукции - тесла, магнитного потока - вебер, индуктивности - генри. При этом не меняются и понятия упомянутых величин.

Однако имеются электрические и магнитные величины, для которых рационализация не проходит бесследно: изменяется размер единиц этих величин или понятие самих величин. В частности, изменены единицы величин: магнитной постоянной ([μ₀] = [μʹ₀]/4π), электрического смещения ([D] = 4π[Dʹ]), напряженности магнитного поля ([Н] = 4π[Hʹ]), магнитодвижущей силы ([F] = 4π[Fʹ]), магнитного сопротивления ([r_m] = 4π·[rʹ_m]), магнитного заряда ([m] = [mʹ]/4π), магнитного момента ([p_m] = [pʹ_m]/4π) и др.

Уравнения электромагнитного поля в рационализованной и нерационализованной формах приведены в табл. 10.

⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨

МЕНЮ САЙТА / СОДЕРЖАНИЕ