Ł Старые понятные учебники советских времен по физике, математике. Акупунктура, похудение

ЧЕРТОВ А.Г. "ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН", 1977

Групповая скорость. Скорость распространения реальной волны, представляющей группу синусоидальных волн, в среде, обладающей дисперсией, называется групповой скоростью. Она определяется по формуле

u = v - λ dv/dλ, (10.11)

где v - фазовая скорость волны, λ - длина волны, dv/dλ - величина, выражающая зависимость фазовой скорости от длины волны.

Из этой формулы следует, что групповая скорость выражается в тех же единицах, что и фазовая скорость, т.е. в метрах в секунду, и имеет размерность

dim u = LT^-1.

Волновое число. Волновое число - величина, равная числу длин волн, укладывающихся на единице длины, т.е.

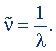(10.12)

Положив λ = 1 м, найдем единицу волнового числа

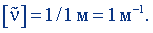
Метр в минус первой степени равен волновому числу, при котором на отрезке длиной 1 м укладывается одна волна. Размерность волнового числа:

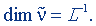
Волновым числом k называют также величину, связанную с длиной волны соотношением

k = 2π/λ. (10.13)

Вектор k, численно равный волновому числу k, совпадающий по направлению с лучом бегущей волны, называют волновым вектором.

Волновое число, понимаемое и в этом втором смысле, также выражается в метрах в минус первой степени и имеет размерность L^-1.

Время релаксации. Время релаксации - величина, равная времени, в течение которого амплитуда колебаний уменьшается в е = 2,718... раз. Поэтому время релаксации τ обратно коэффициенту затухания:

τ = 1/δ. (10.14)

Положив δ = 1 с^-1, получим

[τ] = 1/1 c^-1 = 1 с.

Время релаксации выражается в секундах. Размерность времени релаксации:

dim τ = Т.

Добротность колебательного контура. Добротность Q колебательного контура - величина, равная отношению амплитуды напряжения на конденсаторе контура при резонансе к амплитуде внешней э. д. c., т.е.

Q = U₀/Ɛ₀. (10.15)

Положив U₀ = 1 В, Ɛ₀ = 1 В, найдем единицу добротности контура:

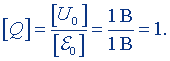
Следовательно, добротность контура выражается в безразмерных единицах. Размерность добротности

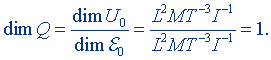
Затухание колебательного контура. Затуханием d колебательного контура называют величину, обратную его добротности, т.е.

d = 1/Q. (10.16)

Затухание контура, как и добротность, выражается в безразмерных единицах.

Энергия волн. Как и любая другая энергия, энергия волн выражается в джоулях.

Объемная плотность энергии волн. Энергия волн распределяется в пространстве неравномерно и, кроме того, меняется во времени. Распределение энергии волн в пространстве в некоторый момент времени характеризуется объемной плотностью энергии

w = dW/dV, (10.17)

где dW - энергия, заключенная в бесконечно малом объеме dV, а также средней объемной плотностью энергии

<w> = W/V, (10.18)

где W - энергия волн, заключенная в элементе пространства объемом V, линейные размеры которого много больше длины волны λ.

Из (10.18) определим единицу объемной плотности энергии воли, положив W = 1 Дж, V = 1 м³:

[w] = 1 Дж/1 м³ = 1 Дж/м³.

Эта единица называется джоуль на кубический метр. Размерность объемной плотности энергии волн:

dim w = L^-1MT^-2.

Поток энергии волн. Поток энергии Ф есть величина, равная энергии ΔW, перенесенной волнами через некоторую поверхность, ко времени Δt, за которое эта энергия перенесена (предполагается, что Δt ≫ T, где Т - период колебаний) *:

Ф = ΔW/Δt. (10.19)

* Поток энергии волн не постоянен во времени. В течение периода колебаний он изменяется от максимального до нуля. Поэтому формула (10.19) выражает не мгновенное, а усредненное по времени значение потока энергии. Пользоваться формулой (10.19) можно лишь в том случае, если поток вычисляется за время, много большее периода колебаний.

Подставив в (10.19) ΔW = 1 Дж, Δt = 1 с, получим единицу потока энергии

[Ф] = 1 Дж/1 с = 1 Дж/с = 1 Вт.

Ватт равен потоку энергии воли, эквивалентному механической мощности 1 Вт. Размерность потока энергии

dim Ф = L²MT^-3.

Плотность потока энергии волн (интенсивность волн). Плотностью потока I энергии волн называют величину, равную отношению потока энергии Ф к площади S поверхности, расположенной перпендикулярно направлению распространения волн, т.е.

I = Ф/S. (10.20)

Положив Ф = 1 Вт, S = 1 м², найдем единицу плотности потока энергии:

[I] = 1 Вт/1 м² = 1 Вт/м².

Ватт на квадратный метр равен плотности потока энергии волн, при которой через поверхность площадью 1 м², расположенную перпендикулярно направлению распространения волн, за время 1 с переносится энергия 1 Дж. Размерность плотности потока энергии:

dim I = МТ^-3.

§ 11. ПРОИЗВОДНЫЕ ЕДИНИЦЫ АКУСТИЧЕСКИХ ВЕЛИЧИН

Существует два вида акустических величин: 1) величины, характеризующие звук как физическое явление волнообразного распространения колебаний частиц упругой среды. К ним относятся скорость звука, звуковое давление, звуковая энергия, плотность звуковой энергии и др.; 2) величины, характеризующие звук как специфическое ощущение, вызываемое действием звуковых волн на орган слуха. К ним относятся уровень громкости, частотный интервал и др. Между теми и другими величинами существует определенная зависимость. Например, частотный интервал связан с частотой звука, уровень громкости является функцией интенсивности звука и его частоты и т.д.

Для акустических величин первого вида установлены единицы, входящие в Международную систему и систему СГС; величины второго вида выражаются во внесистемных единицах.

Рассмотрим акустические единицы СИ.

Скорость звука. Скорость звука есть фазовая скорость звуковых волн в упругой среде и, как любая скорость, выражается в метрах в секунду (м/с) и имеет размерность:

dim c = LT^-1.

Звуковое давление. Звуковым давлением р называют давление, дополнительно возникающее в газообразной или жидкой среде при прохождении через нее звуковых волн. Звуковое давление - величина переменная, меняющаяся периодически с частотой, равной частоте звуковых волн. В данной точке звукового поля в течение периода звуковых колебаний давление меняется по синусоидальному закону:

р = р₀ sin ωt,

где ω = 2π/T - круговая частота, р₀ - амплитуда давления (максимальное звуковое давление).

Звуковое давление, как и любое другое давление, выражается в паскалях и имеет размерность:

dim p = L^-1MT^-2.

Единицу звукового давления можно получить по формуле амплитуды звукового давления:

р₀ = ωcρA, (11.1)

где ω - циклическая частота, с - скорость звука, ρ - плотность среды, в которой распространяется звук, А - амплитуда колебаний ее частиц.

Положив в формуле (11.1) ω = 1 с^-1, с = 1 м/с, ρ = 1 кг/м³, А = 1 м, найдем единицу звукового давления:

[p] = 1 с^-1 · 1 м·с^-1 · 1 кг·м^-3 · 1 м = 1 Н/м² = 1 Па.

Колебательная скорость. Колебательной скоростью v звука называют величину, равную произведению амплитуды А колебаний частиц среды, через которую проходит звук, на круговую частоту ω колебаний, т.е.

w = Aω. (11.2)

Положив А = 1 м, ω = 1 с^-1, получим единицу колебательной скорости:

[v] = 1 м · 1 с^-1 = 1 м/с.

Размерность колебательной скорости:

dim v = LT^-1.

Объемная скорость звука. Объемной скоростью V звука называют величину, равную произведению колебательной скорости v на площадь S поперечного сечения канала, в котором распространяется звук:

V = vS. (11.3)

Подставив в (11.3) v = 1 м/с, S = 1 м², найдем единицу объемной скорости звука:

[V] = 1 м·с^-1 · 1 м² = 1 м³/с.

Кубический метр в секунду равен объемной скорости звука при колебательной скорости 1 м/с и площади поперечного сечения канала 1 м². Размерность объемной скорости звука:

dim V = L³T^-1.

Акустическое сопротивление. Акустическое сопротивление - величина, характеризующая свойства среды как проводника и потребителя звуковой энергии, аналогичная понятию сопротивления электрической цепи. В акустике, аналогично закону Ома I = U/r, имеет место соотношение, которое устанавливает зависимость объемной скорости V звука от амплитуды р₀ звукового давления:

V = р₀/Z_a. (11.4)

Величину Z_a называют акустическим сопротивлением. Из формулы (11.4) запишем

Z_a = р₀/V. (11.5)

Положив р₀ = 1 Па, V = 1 м³/с, получим единицу акустического сопротивления:

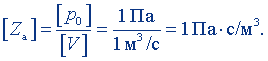
Паскаль-секунда на кубический метр равна акустическому сопротивлению области звукового поля, в которой объемная скорость 1 м³/с создается при звуковом давлении

1 Па. Размерность акустического сопротивления

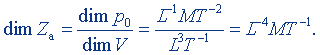
Удельное акустическое сопротивление. Акустическое сопротивление Z_a канала, в котором распространяется звук, обратно пропорционально площади его поперечного сечения. Для канала, имеющего всюду одинаковое сечение S,

Z_a = Z_S/S,

где Z_S - удельное акустическое сопротивление. Отсюда получим

Z_S = Z_aS, (11.6)

т.е. удельное акустическое сопротивление - величина, равная произведению акустического сопротивления канала на площадь его поперечного сечения.

Положив в (11.6) Za = 1 Па·с/м³, S = 1 м², найдем единицу удельного акустического сопротивления:

[Z_S] = 1 Па·с/м³ · 1 м³ = 1 Па·с/м.

Паскаль-секунда на метр равна удельному акустическому сопротивлению области звукового поля, которая при площади поперечного сечения 1 м³ имеет акустическое сопротивление 1 Па·с/м³. Размерность удельного акустического сопротивления:

dim Z_S = L^-2MT^-1.

Механическое сопротивление. Механическим сопротивлением называют величину, равную отношению силы F, действующей на некоторое поперечное сечение (например, поперечное сечение канала, в котором распространяется звук), к средней колебательной скорости <v> в этом сечении,

Z_m = F/<v>. (11.7)

Положив F = 1 Н, <v> = 1 м/с, получим единицу механического сопротивления:

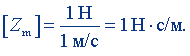
Ньютон-секунда на метр равна механическому сопротивлению области звукового поля, в котором колебательная скорость 1 м/с возникает при силе 1 Н. Размерность механического сопротивления:

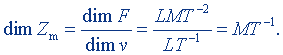
Звуковая энергия. Частицы упругой среды, в которой распространяются звуковые волны, совершают колебательные движения и поэтому обладают энергией, которую называют звуковой. Звуковая энергия W, как и любая другая энергия, выражается в джоулях.

Джоуль - звуковая энергия, эквивалентная механической работе 1 Дж. Размерность звуковой энергии

dim W = L²MT^-2.

Плотность звуковой энергии. Физическую величину, равную отношению звуковой энергии ΔW, содержащейся в некоторой области звукового поля, к объему ΔV этой области, называют плотностью звуковой энергии и определяют по формуле

w = ΔW/ΔV. (11.8)

Положив ΔW = 1 Дж, ΔV = 1 м³, получим единицу плотности звуковой энергии

[w] = 1 Дж/1 м³ = 1 Дж/м³.

Джоуль на кубический метр равен плотности звуковой энергии, при которой в области звукового поля объемом 1 м³ содержится звуковая энергия 1 Дж. Размерность плотности звуковой энергии:

dim w = L^-1MT^-2.

⇦ Ctrl предыдущая страница / следующая страница Ctrl ⇨

МЕНЮ САЙТА / СОДЕРЖАНИЕ